Aurélie 16/04/07
 

bac Inde 2007 : charge et décharge d'un super condensateur : aspect énergétique( 5pts)

lycée-francais-pondichery

Google

 

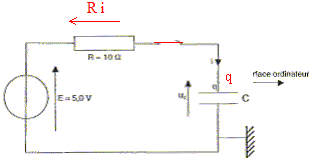
I. Charge d'un condensateur à l'aide d'une source de tension constante : on dispose d'un condensateur sur lequel le fabriquant a indiqué "1 F". Pour vérifier la valeur de la capacité, on réalise le circuit suivant :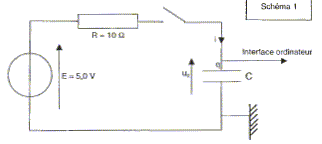

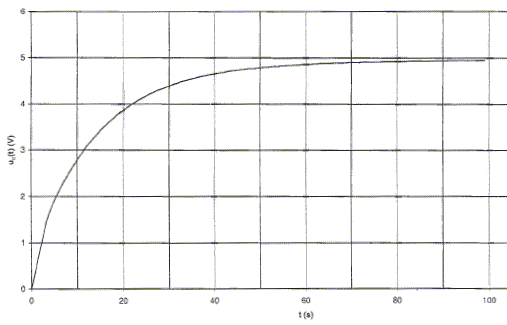
A l'instant t=0, on ferme l'interrupteur et on relève la tension aux bornes du condensateur. On obtient la courbe suivante :

  1. En utilisant la loi d'additivité des tensions, établir la relation qui existe entre uC(t) et sa dérivée par rapport au temps ( équation différentielle vérifiée par uC).
  2. Vérifier que uC(t)=E(1-exp(-t/t)) est solution de l'équation différentielle et vérifie la condition initiale uC(0) = 0. Déterminer l'expression de t en fonction des caractèristiques du circuit.
  3. A partir de l'enregistrement et par une méthode de votre choix déterminer la capacité C du condensateur. Comparer avec la valeur donnée par le fabriquant.

II. Restitution de l'énergie et décharge à courant constant : On prendra C= 1,0 F.

Le condensateur est incorporé au montage suivant :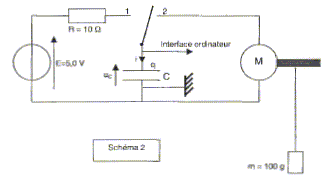

M est un moteur sur lequel est enroulé une ficelle soutenant à son extrémité une masse m= 100 g.

  1. A l'instant t=0, pris comme nouvelle origine des temps, on bascule l'interrupteur en voie 2. Le condensateur se décharge et le moteur se met en mouvement entraînant la charge m =100 g. Celle-ci monte d'une hauteur h= 3,10 m en 18 s. Les valeurs enregistrées par le logiciel sont les suivantes :
    t=0 ( démarrage du moteur) ; uC(0)=4,9 V ; t=18 s ( arrêt du moteur), uC(18)= 1,5 V.
    L'enregistrement de uC(t) par le logiciel donne une courbe qui peut être assimilée à une droite représentée par uC(t) = a t+b avec a<0 et b>0.
    - Calculer les valeurs numériques des constantes a et b.
  2. Déterminer l'expression de la charge instantanée q(t) du condensateur en fonction du temps. En déduire la valeur de l'intensité du courant i. Que pensez-vous du signe de i ?
  3. Calculer successivement :
    - l'énergie stockée dans le condensateur à t=0.
    - l'énergie restant à t = 18 s.
    - l'énergie cédée par le condensateur.
    - l'énergie mécanique '( potentielle) reçue par la masse ( g= 9,8 m/s²)
    - le rendement du dispositif.
I. Charge d'un condensateur à l'aide d'une source de tension constante

additivité des tensions : R i + uC=E avec i = dq/dt et q = CuC ; d'où i = C duC/dt

RCduC/dt + uC=E ; duC/dt +1/(RC) uC=E/(RC) (1)

Vérifions que uC(t)=E(1-exp(-t/t)) est solution de l'équation différentielle :

duC/dt = E/t exp(-t/t) ; repport dans (1) : E/t exp(-t/t) + 1/(RC)[E(1-exp(-t/t))]= E/(RC)

Cette égalité est vérifiée quel que soit t si : t =RC.

uC(0)=E(1-exp(-0/t)) = E(1-1) = 0. La condition initiale uC(0) = 0 est vérifiée.

C= t/R avec R= 10 W soit C= 11/10 = 1,1 F , valeur du même ordre de grandeur que celle donnée par le fabriquant.

II. Restitution de l'énergie et décharge à courant constant :

L'enregistrement de uC(t) par le logiciel donne une courbe qui peut être assimilée à une droite représentée par uC(t) = a t+b avec a<0 et b>0.

Valeurs numériques des constantes a et b :

t=0 ( démarrage du moteur) ; uC(0)=4,9 V ; t=18 s ( arrêt du moteur), uC(18)= 1,5 V

uC(0)=4,9 =a*0 + b ; b= 4,9 V.

uC(18)= 1,5 = a*18+4,9 ; a = -0,19 V s-1.

Expression de la charge instantanée q(t) du condensateur en fonction du temps :

q(t) = C uC(t) ave C= 1,0 F ; q(t) = -0,19 t +4,9.

Intensité du courant i : i(t) = dq(t) / dt = -0,19 A.

Le signe moins traduit le fait que le courant a le sens contraire au courant de charge.

Energie stockée dans le condensateur à t=0 : ½CUc2(0) = 0,5*4,92 = 12 J.

Energie restant à t = 18 s : ½CUc2(18) = 0,5*1,52 = 1,1 J.
Energie cédée par le condensateur : ½CUc2(0) -½CUc2(18) =10,87 J ( réponse 11 J)
Energie mécanique ( potentielle) reçue par la masse m : mgh = 0,1*9,8*3,1 = 3,0 J.
Rendement du dispositif : 3/10,87 *100 = 28 %.
 

retour -menu