Ondes : le GPS et les horloges : bac S Polynésie 09/04

Les ondes :

De nombreuses activités humaines demandent un repérage précis (latitude, longitude, altitude) sur le globe terrestre ou dans son voisinage.

Les ondes radio sont des ondes électromagnétiques comme les ondes lumineuses et se propagent à la célérité c = 3,00 10⁸ m.s^-1 dans le vide.

Les satellites du système GPS émettent des signaux codés sous forme d'ondes radio émises sur deux fréquences différentes (1,6 et 1,2 GHz) et dont la réception au sol va permettre de calculer la position.

Longueurs d'onde dans le vide des ondes émises par les satellites :

l = c / f avec f : fréquence en Hz ; c, célérité en m/s, l : longueur d'onde en m.

Pour f = 1,6 10⁹ Hz : l₁ = 3,00 10⁸ / 1,6 10⁹ =0,1875 m soit l₁ = 0,19 m.

Pour f = 1,2 10⁹ Hz : l₂ = 3,00 10⁸ / 1,2 10⁹ = 0,25 m.

Durée t mise par le signal pour aller du satellite S au récepteur R si le satellite est situé à la verticale de R à l'altitude h= 20 180 km :

t = h / c avec h : distance RS en m ; c : célérité en m/s et t: durée en s.

h = 2,018 10⁷ m ; t = 2,018 10⁷ / 3,00 10⁸ = 6,73 10^-2 s.

Pour une mesure unique, l'erreur sur la distance verticale est de 20 m en standard.

Calcul (en nanosecondes) de l'erreur Dt sur la durée de propagation du signal :

t = h/c ; Dt / t = Dh / h soit Dt = Dh t / h = Dh / c

Dt = 20 * 6,73 10^-2 / 2,018 10⁷ = 6,7 10^-8 s = 67 ns.

La durée t de propagation du signal est environ 10⁶ fois plus grande que l'erreur Dt.

L'erreur sur la distance verticale sera d'autant plus petite que la mesure de t sera plus précise.

L'atmosphère est un milieu dispersif pour l'onde radio : la célérité de l'onde dépend de la fréquence.

La fréquence de l'onde restant constante, tandis que la célérité et la longueur d'onde varient.

 Dans une horloge à balancier, pour une faible amplitude a, la période T vérifie la relation T = T₀ ( 1+a²/16)

avec T₀ = 2p(l/g)^½ où l est la longueur du balancier et g l'intensité du champ de pesanteur, a est en radian.

Par analyse dimensionnelle, que (l/g)^½ est homogène à une durée :

l est une longueur : [ l ]= L

g est une accélération, soit une longueur divisée par le carré d'une durée : [g]=L T^-2.

[ l / g ] = T² ; [ (l/g)^½ ] = T.

T = T₀ ( 1+a²/16) ; DT/ T₀ =(T-T₀ ) /T₀= a²/16

4 degrés = 4 *3,14 / 180 = 6,98 10^-2 rad

DT/ T₀ = (6,98 10^-2)²/16 = 3,0 10^-4.

Calcul de la période T₂ d'une horloge identique de même longueur en un lieu où g₂ = 9,800 N.kg^-1 en conservant la même amplitude :

T₁ = 2p ( l/g₁)^½ ; T₂ = 2p ( l/g₂)^½ ; T₂ / T₁ = ( g₁ /g₂)^½ ; T₂ = T₁ ( g₁ /g₂)^½.

T₂ = 2,000 ( 9,810 /9,800)^½ = 2,001 s.

En conséquence, une horloge à balancier ne convient pas pour déterminer une longitude. ( Quand le bateau change de latitude au cours de son voyage, la valeur de g change ).

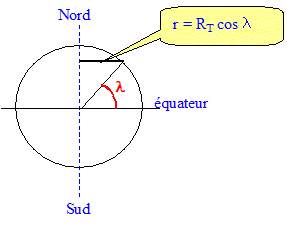
Calcul de la précision de l'horloge :

156 jours = 156*24*3600 secondes = 1,35 10⁷ s.

15 / 1,35 10⁷ = 1,1 10^-6.

Distance, en kilomètres, calculée sur le parallèle de Plymouth, correspondantaux 15 s de dérive observées lors du voyage de John Harrison :

La latitude de Plymouth est de 50° nord. Rayon de la Terre : R_T = 6380 km

On rappelle que la latitude l d'un point P est l'angle entre le plan de l'équateur et la droite joignant P au centre de la Terre. Un parallèle est un cercle de rayon r à la surface de la Terre. Tous les points de ce cercle sont à la même latitude l.

r = 6380 cos 50 = 4100 km.

Un point situé à la surface de la Terre à la latitude de Plymouth décrit une circonférence de rayon r en 24 heures ( 86400 s)

valeur de la circonférence 2pr = 2*3,14*4100 = 2,6 10⁴ km

dérive : 2,6 10⁴ * 15 / 86400 = 4,4 km.

Cette dérive est suffisamment importante pour conduire à un naufrage si la visibilité est mauvaise.