|
L'élément iode : oxtdo-réduction ; cinétique : spectrophotométrie ; électrolyse bac S 09/ 2007 France |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
En 1811, le salpêtrier Courtais observe des fumées violettes lors de la calcination du goémon en Bretagne. C'est Gay-Lussac, en 1813, qui donnera son nom à ce nouvel élément : iode, du grec iodos signifiant violet. L'élément iode est présent en très faible quantité dans l'eau de mer (environ 50 µg par litre). Pendant longtemps, il fut extrait des algues qui concentrent cet élément dans leurs tissus. Aujourd'hui cet élément présente un regain d'intérêt. Des recherches sur la production de dihydrogène s'inscrivant dans une stratégie d'économie des énergies fossiles et de limitation de la production de gaz à effet de serre utilisent un procédé dans lequel intervient l'iodure d'hydrogène (HI). Données : Le diiode ( I2) se présente sous la forme d'un solide gris-violet à l'éclat métallique. L'ion iodure ( I-) est incolore en solution. Le diiode est très peu soluble dans l'eau. En présence d'ions iodure, il est sous forme d'ions triiodure (I3- ) solubles dans l'eau et de couleur brune. La solution ainsi obtenue est brune. Par souci de simplification, on notera, dans tous les cas, le diiode en solution I2 (aq). Couples oxydant/réducteur : IO3-(aq) / I2(aq) ; I2(aq) / I- (aq) ; SO42-(aq) / HSO3-(aq) ; HSO4-(aq) / SO2(aq) ; O2(g) / H2O(l) ; H+(aq)/H2(g) Couples acide/base : HI(aq) / I- (aq) ; HSO3-(aq)/ SO32-(aq) ; H2SO4(aq)/HSO4-(aq) ; HSO4-(aq) /SO42-(aq) ; H2O(l) /HO-(aq). Une réaction pour obtenir du diiode : Actuellement, le procédé le plus courant de fabrication du diiode se fait à partir du nitrate du Chili. Ce nitrate naturel est utilisé pour obtenir des engrais. Lors de la préparation des engrais, des eaux de rinçage sont recueillies. Ces eaux contiennent des ions iodate IO3- qu'on fait réagir avec les ions hydrogénosulfite HSO3- . La transformation peut être modélisée par l'équation suivante : 2IO3- (aq) + 5 HSO3- (aq) + 2H2O(l) = 5 SO42-(aq) + I2(aq) + 3H3O+.
IO3-(aq) / I2(aq) et SO42-(aq) / HSO3-(aq) La réaction de synthèse du diiode est donc une réaction d'oxydoréduction . Expression de la constante d'équilibre de cette transformation : K = [SO42-(aq)]5 [I2(aq)] [H3O+]3 / ( [HSO3- (aq)]5 [IO3- (aq) ]2 ) Les ions oxonium H3O+ figurent dans le membre de droite de l'équation ; en conséquence : - l'ajout d'ion oxonium, d'une solution acide, déplace l'équilibre dans le sens indirect ( vers la gauche) : consommation des ions apportés. - la diminution des ions oxonium ( ajout d'une solution basique ) déplace l'équilibre dans le sens direct ( vers la droite) : formation d'ion oxonium. Le pH de l'eau utilisée a donc une incidence sur l'évolution de l'équilibre.
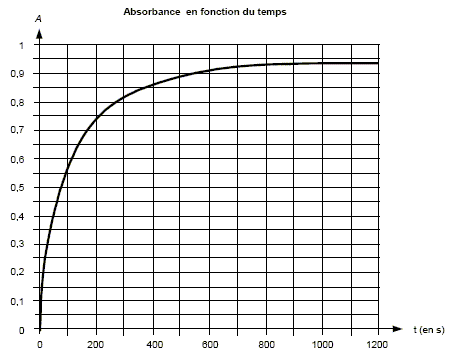
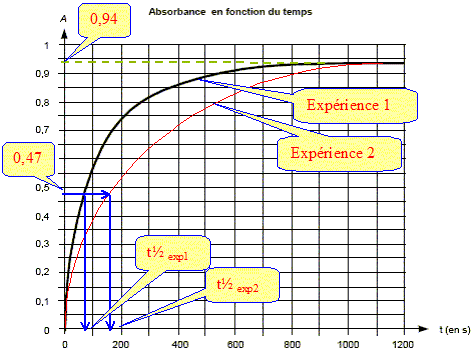
On désire étudier l'évolution temporelle de la réaction d'oxydation des ions iodure par le peroxyde d'hydrogène (H2O2) par suivi spectrophotométrique. L'équation de la réaction modélisant la transformation étudiée est : H2O2 (aq) + 2I-(aq) + 2H3O+ = I2(aq) + 4H2O(l) On dispose des solutions suivantes : SA : solution d'acide sulfurique dont la concentration en ions oxonium est cA = 0,10 mol/L SB : solution d'iodure de potassium dont la concentration en ions iodure est cB = 0,10 mol/L SC : solution de peroxyde d'hydrogène dont la concentration est cC = 0,10 mol/L. Lors des expériences décrites ci-dessous, la seule réaction chimique faisant intervenir les ions iodure est celle écrite ci-dessus. Première expérience : Á l'aide d'une solution témoin, on règle le spectrophotomètre à une longueur d'onde adaptée pour l'étude de l'absorption par le diiode. Seul le diiode absorbe à cette longueur d'onde. On rappelle que d'après la loi de Beer-Lambert, l'absorbance A est proportionnelle à la concentration de l'espèce absorbante. On mélange VA = 30,0 mL de la solution SA avec VB = 60,0 mL de la solution SB. À l'instant de date t = 0 s, on déclenche le chronomètre et on ajoute VC = 10,0 mL de solution SC. Rapidement on homogénéise et on verse quelques millilitres du mélange dans une cuve qu'on place dans le spectrophotomètre. On obtient la courbe suivante.
On rappelle la définition de la vitesse volumique d'une réaction : v= 1/V dx/dt où V est le volume total du mélange réactionnel.
Réponse : tableau d'évolution du système :
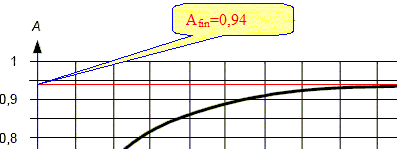
La transformation étant considérée comme totale, l'avancement final est égal à l'avancement maximal. Si H2O2 (aq) est en défaut : 1,0 10-3-xf = 0 soit xf = 1,0 10-3 mol. Si I-(aq) est en défaut : 6,0 10-3-2xf = 0 soit xf = 3,0 10-3 mol. Si H3O+ est en défaut : 3,0 10-3-2xf = 0 soit xf = 1,5 10-3 mol. On retient la plus petite valeur : xf = 1,0 10-3 mol. L'état final est atteint à t = 1200 s : La tangente à la courbe A=f(t) à la date t = 1200 s est une droite horizontale. Le coefficient directeur de cette droite est donc nul : [dA/dt] 1200=0. L'absorbance A est proportionnelle à la concentration de l'espèce absorbante : A = k [I2(aq)] donc [d [I2(aq)] / dt ]1200=0. [I2(aq)]1200 est constante. Le quotient de l'avancement x par l'absorbance A est constant : L'absorbance A est proportionnelle à la concentration de l'espèce absorbante : A = k [I2(aq)] , k étant une constante. [I2(aq)] = x / (VA + VB+VC)= x / V. A = kx / V ; r = x/A = V/k Le volume total du mélange étant constant, le rapport de l'avancement par l'absorbance est constant.
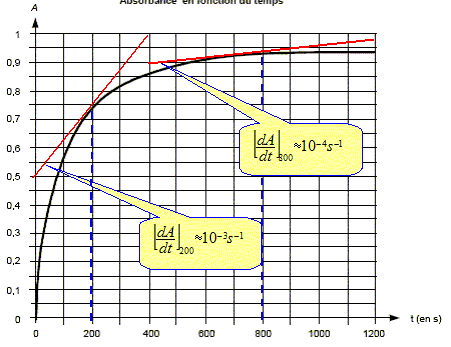
r = xf/Af = 1,0 10-3 / 0,94 = 1,1 10-3 mol. Expression de la vitesse de réaction v en fonction du rapport r, du volume V et de la dérivée de l'absorbance par rapport au temps dA/dt : v =1/V dx/dt ; d'autre part : x= r A avec r une constante : dx/dt = r dA/dt. v = r/V dA/dt. Comparaison des vitesses volumiques de la réaction aux instants t1 = 200 s et t2 = 800 s :
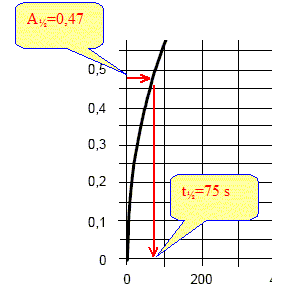
La vitesse est proportionnelle à dA/dt ; dA/dt représente le coefficient directeur de la tangente à la courbe à la date considérée. La vitesse à t2=800 s est bien plus faible qu'à la date t1 = 200 s. Le temps de demi-réaction : Le temps de demi réaction t½ est le temps au bout duquel l'avancement est égal à la moitié de l'avancement final. Or l'avancement et l'absorbance sont proportionnel donc At½ =½ Afin = 0,94 / 2 = 0,47.
Deuxième expérience : On refait la même étude en utilisant 30,0 mL de solution SA, 30,0 mL de solution SB, 10,0 mL de solution SC et 30,0 mL d'eau distillée.
Réponse : La concentration de l'un des réactifs, l'iodure de potassium a changé, diminué, dans l'expéreince 2 :
Si I-(aq) est en défaut : 3,0 10-3-2xf = 0 soit xf = 1,5 10-3 mol. Si H3O+ est en défaut : 3,0 10-3-2xf = 0 soit xf = 1,5 10-3 mol. On retient la plus petite valeur : xf = 1,0 10-3 mol. Le réactif limitant n'a donc pas changé. Comparaison des temps de demi-réaction des deux expériences : La concentration des réactifs est un facteur cinétique : si l'une des concentration des réactifs diminue ( les autres restant inchangées), alors la vitesse de la réaction diminue et l'état final inchangé sera atteint au bout d'un temps plus élévé. Le temps de demi- réaction dans l'expérience 2 sera plus grand que dans l'expérience 1.
Gay-Lussac étudia les propriétés de l'élément iode et constata de nombreuses analogies avec l'élément chlore. En particulier il synthétisa un gaz, l'iodure d'hydrogène (HI ) dont les propriétés sont très proches de celles du chlorure d'hydrogène. Dans un laboratoire, on a fabriqué un litre d'une solution S1 en dissolvant une quantité de matière n1 = 5,0 10-2 mol d'iodure d'hydrogène dans l'eau. L'iodure d'hydrogène réagit totalement avec l'eau et on obtient une solution qui contient des ions iodure et des ions oxonium. Les concentrations molaires volumiques des ions iodure et oxonium dans la solution ainsi fabriquée sont [H3O+(aq)] = [I-(aq)] = 5,0 10-2 mol/L. On utilise la solution S1 pour faire une électrolyse. Dans un becher on verse 100,0 mL de solution S1, puis on plonge deux électrodes inattaquables reliées à un générateur de tension constante. Données : Couples oxydant / réducteur : I2(aq) / I- (aq) ; O2(g) / H2O(l) ; H+(aq)/H2(g) Volume molaire des gaz dans les conditions de l'expérience : VM = 25 L.mol-1. Quantité d'électricité transportée par une mole d'électrons : F = 9,65 104 C.mol-1.
Réponse :
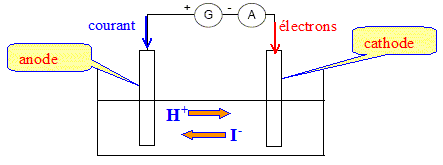
Les électrons sont les porteurs de charges dans les métaux ; les ions en solution sont les porteurs de charges. Equations électrochimiques modélisant les transformations susceptibles de se produire à chaque électrode : Oxydation à l'anode positive : 2I- (aq) = I2(aq) + 2e- H2O(l) = ½O2(g) + 2H+ (aq) + 2e- Réduction à la cathode négative : 2H+(aq)+ 2e- =H2(g) Sachant qu'il n'y a pas de dégagement gazeux à l'anode, le diiode se dépose à l'anode ; le dihydrogène se dégage à la cathode. Quantité d'électricité qui a traversé le circuit pendant cette électrolyse : Q=IGDt = 0,25*30*60 = 4,5 102 C. Quantité de matière d'électrons correspondante : La charge ( en valeur absolue) d'une mole d'électrons est 9,65 104 C. n(e-) = 450 /9,65 104 = 4,663 10-3 mol ( 4,7 10-3 mol) Volume de gaz recueilli à la cathode : D'après l'équation 2H+(aq)+ 2e- =H2(g) la quantité de matière de dihydrogène vaut : ½n(e-) =0,5* 4,663 10-3 = 2,332 10-3 mol volume (L) = quantité de matière (mol) * volume molaire (L/mol) V= 2,332 10-3 *25 = 5,8 10-2 L. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|