découvertes liées à des éclipses du soleil, ondes, spectres d'émission bac S 2007 France

Partition lunaire :

Des chercheurs du CEA de l'équipe d'Elisabeth Blanc viennent d'annoncer qu'une éclipse n'a pas pour seul effet une baisse de la luminosité. Lors de l'éclipse du Soleil du 11 août 1999, à 12 h 16 précises, l'ombre de la Lune commence sa traversée de la France à la vitesse de 2850 km/h sur un axe Cherbourg-Strasbourg. Sur son passage, la température de l'air chute rapidement d'environ 5°C. Le déplacement de cette zone froide, à la même vitesse que celui de l'ombre (...), engendre dans son sillage des ondes transversales dont la fréquence est largement inférieure à 20Hz.

D'après la revue Les Défis du CEA - n°97 octobre-novembre 2003.

Ondes créées lors de l'éclipse :

Définir une onde mécanique progressive.

Définir une onde transversale.

Dire, en justifiant la réponse, si les ondes créées lors de l'éclipse peuvent être sonores.

Caractéristiques des ondes créées :

L'équipe en charge du projet a pu détecter à faible altitude, une série d'ondes dont la période moyenne est de l'ordre de 10 minutes et la célérité moyenne est de l'ordre de 100 km/h.

Vérifier que la fréquence de l'onde est effectivement largement inférieure à 20Hz.

Ces ondes peuvent-elles être diffractées par des montagnes séparées par une distance de 10 km ? Justifier la réponse.

Aide aux calculs : 1/6= 0,17 ; 1/36 = 2,8 10^-2.

Une onde mécanique progressive est la propagation d'une perturbation ( modification de l'une des propriétés du milieu) dans un milieu matériel, avec transport d'énergie, sans transport de matière.

L'onde est transversale si la direction de propagation de l'onde et la direction de la perturbation sont perpendiculaires.

"engendre dans son sillage des ondes transversales"

Les ondes créées lors de l'éclipse ne peuvent pas être sonores, car les ondes sonores sont des ondes progressives longitudinales.

L'équipe en charge du projet a pu détecter à faible altitude, une série d'ondes dont la période moyenne est de l'ordre de 10 minutes et la célérité moyenne est de l'ordre de 100 km/h.

Fréquence de l'onde :

La fréquence ( Hz) est l'inverse de la période exprimée en seconde.

T= 10*60 = 600 s ; f = 1/600 = 1/6 10^-2 = 0,17 10^-2 = 1,7 10^-3 Hz , valeur bien inférieure à 20 Hz.

Longueur d'onde l :

l = v/ f avec v = 100 / 3,6 m/s ; v= 1000/36 = 1000*2,8 10^-2 = 28 m/s.

l = 28 / 1,7 10^-3 = 28 10³ / 1,7 de l'ordre de 10⁴ m.

Des montagnes séparées par une distance de 10 km ( 10⁴ m) peuvent diffractées ces ondes : la longueur d'onde est du même ordre de grandeur que la distance séparant les montagnes.

Lors de l'éclipse totale du Soleil du 18 août 1868, le français Pierre Janssen et le britannique Norman Lockyer ont analysé le spectre de la couronne solaire et ont remarqué qu'il présentait une raie brillante dans le jaune très proche de celle du sodium. N. Lockyer a émis l'hypothèse que cette raie était due à un nouvel élément qu'il baptisa hélium (du grec hélios qui signifie Soleil). Ce n'est que vingt-sept ans plus tard que cet élément chimique fut identifié sur Terre.

Célérité de la lumière dans le vide : c = 2,998 10⁸ m/s ; constante de Planck : h = 6,626 10^-34 J.s ; 1 eV = 1,602 10^-19 J ;

Longueur d'onde de la raie D du sodium dans le vide : l_Na = 589,0 nm.

Longueur d'onde de la raie jaune de l'hélium dans le vide : l _He = 587,6 nm.

Aide aux calculs : 6,626*2,998*1,602/589 = 5,403 10^-2 ; 6,626*2,998/(1,602*587,6 )= 2,110 10^-2 ;

6,626*2,998/(1,602*589 )= 2,105 10^-2 ; 6,626*2,998*1,602/587,6 = 5,416 10^-2.

Spectre d'énergie

Illustrer, en s'aidant d'un schéma de niveaux d'énergie d'un atome, le phénomène d'émission d'un photon (quantum d'énergie lumineuse).

On note E l'énergie du photon émis lors d'une transition énergétique d'un atome. Donner l'expression littérale de E en fonction de la longueur d'onde l de la radiation lumineuse émise dans le vide, de la constante de Planck h et de la célérité de la lumière dans le vide c.

Raie D du sodium

Calculer la valeur de E en électronvolts, pour le rayonnement correspondant à la raie D du sodium.

Déterminer, en s'aidant de la figure ci-dessous, à quelle transition correspond cette émission.

L'énergie du photon correspond à l'émission de la raie jaune de l'hélium (de longueur d'onde l _He ) est égale à 2,110 eV. En s'aidant de la figure ci-dessous, justifier que cette émission ne peut pas être attribuée au sodium.

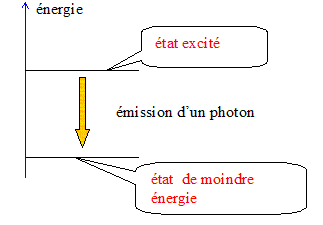
 Spectre d'énergie

Schématisons le phénomène d'émission d'un photon :

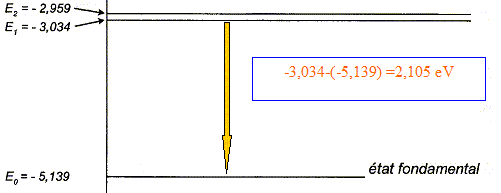
On note E l'énergie du photon émis lors d'une transition énergétique d'un atome.

Expression littérale de E

en fonction de la longueur d'onde l de la radiation lumineuse émise dans le vide, de la constante de Planck h et de la célérité de la lumière dans le vide c.

E= hc/ l.

Valeur de E en électronvolts, pour le rayonnement correspondant à la raie D du sodium :

E = 6,626 10^-34* 2,998 10⁸ / (589,0 10^-9 )= [6,626 *2,998 / 589]* 10^-17 J

Diviser par 1,602 10^-19 pour obtenir l'énergie en eV :

E = [6,626 *2,998 / (1,602*589]* 10² ; E= 2,105 eV.

Transition correspondant à cette émission :

L'énergie du photon correspond à l'émission de la raie jaune de l'hélium (de longueur d'onde l _He ) est égale à 2,110 eV.

Cette émission ne peut pas être attribuée au sodium : 2,110 eV ne correspond à la différence d'énergie entre deux niveaux d'énergie de l'atome de sodium.

Les noyaux d'hélium 3 et d'hélium 4 peuvent être produits par une suite de réactions nucléaires dont les équations sont indiquées ci-dessous :

¹₁H + ¹₁H = ²₁H + ⁰₁e

¹₁H + ²₁H = ³₂He

³₂He + ^x₂He = ⁴₂He+ y ¹₁H

Quel nom donne-t-on à ces réactions nucléaires ?

Parmi les noyaux, ³₂He, ¹₁H et ⁴₂He, lesquels sont isotopes ? Justifier.

Déterminer les valeurs de x et y dans la troisième équation de réaction et justifier la réponse en précisant les lois de conservation utilisées.

On étudie dans la couronne solaire les spectres d'émission des atomes d'hélium 3 et d'hélium 4. On rappelle qu'un spectre atomique caractérise la configuration électronique de l'atome (c'est-à-dire le nuage d'électrons de l'atome).

Ces deux types d'atomes possèdent-ils la même configuration électronique ? Justifier.

Ces deux atomes auraient-ils pu être distingués l'un de l'autre expérimentalement dans le spectre obtenu par Pierre Janssen et Norman Lockyer ?

Des noyaux isotopes ont le même numéro atomique Z, mais des nombres de neutrons différents :

³₂He et ⁴₂He sont donc isotopes.

Valeurs de x et y :

 ³₂He + ^x₂He = ⁴₂He+ y ¹₁H

Conservation de la charge : 2+2 = 2+y d'où y = 2

Conservation du nombre de nucléons : 3+x = 4+2 d'où x = 3.

 Les deux types d'atomes ³₂He et ⁴₂He possèdent la même configuration électronique : ils ont le même nombre de protons, donc le même nombre d'électrons.

Deux atomes ayant la même configuration électronique ont le même diagramme énergétique, donc le même spectre : en conséquence ils n'ont pas pu être distingués par Pierre Janssen et Norman Lockyer.