Aurélie 27/06/07
 

Filtre passe bas bac sti électronique 2007

Google

Le schéma du filtre est représenté ci-dessous. Son étude est d'abord menée en régime sinusoïdal de fréquence f. On adopte la notation complexe où U2 et U3 sont associées aux tensions u2 et u3.

  1. Comment un condensateur se comporte-t-il en très basse fréquence, en très haute fréquence ?
  2. Montrer qu'il s'agit d'un filtre passe-bas.
  3. Établir la fonction de transfert T= U3 / U2 et la mettre sous la forme : T= 1/ ( 1+j f / fc).
    - Donner l'expression de fc en fonction de R3 et C3.
  4. La fréquence fc de l'expression précédente représente la fréquence de coupure à -3 dB du filtre. Sachant que C3 = 100 nF, calculer la valeur de R3 permettant d'obtenir une fréquence de coupure fc de 10 Hz.
  5. Exprimer T (module de T).
    - Calculer la valeur limite T0 de T lorsque f --> 0.
    - Calculer la valeur limite de Too de T lorsque f --> oo.
  6. La tension u2, appliquée à l'entrée du filtre, est maintenant une tension rectangulaire de fréquence f très supérieure à fc dont la décomposition harmonique (limitée aux quatre premiers termes) peut s'écrire :
    u2(t) = <u2> + Û21 sin (wt + q21) + Û23 sin (3wt + q23)
    Expliquer pourquoi on peut considérer u3 = <u2>. 
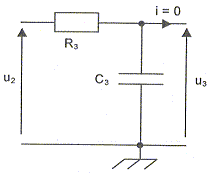
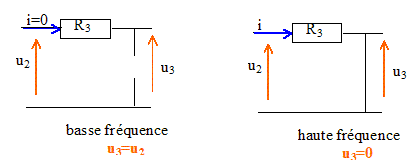
Un condensateur se comporte comme un interrupteur ouvert en très basse fréquence, et comme un interrupteur fermé en très haute fréquence.

Le filtre transmet les basses fréquences : il s'agit d'un filtre passe bas.

Fonction de transfert T= U3 / U2 :

U3 = j/(Cw) i ; U2= U3 +R3 i = (R3 +j/(C3w) ) i

T= U3 / U2 = 1/ [1+jC3R3 w ]

on pose C3R3 = 1/wc ; de plus w= 2 pf et wc = 2 pfc

d'où : T= 1/ ( 1+j f / fc).
Expression de fc en fonction de R3 et C3 :

fc =wc / 2 p = 1/(2 pC3R3 )

Valeur de R3 permettant d'obtenir une fréquence de coupure fc de 10 Hz :

C3 = 100 nF = 10-7 F.

R3 = 1/(2pC3fc) = 1 / ( 6,28 *10-7 *10)= 1,6 105 W.

Expression de T (module de T).

T= ([1-jC3R3 w ])/ [1+(C3R3 w )2] ;

T= [1+(C3R3 w )2]-½.
Valeur limite T0 de T lorsque f --> 0 : T0 = 1

Valeur limite de Too de T lorsque f --> oo : Too = 0

La tension u2, appliquée à l'entrée du filtre, est maintenant une tension rectangulaire de fréquence f très supérieure à fc dont la décomposition harmonique (limitée aux quatre premiers termes) peut s'écrire :
u2(t) = <u2> + Û21 sin (wt + q21) + Û23 sin (3wt + q23)
On peut considérer u3 = <u2> car la valeur moyenne d'une fonction sinus est nulle.
Le circuit de mise en forme :

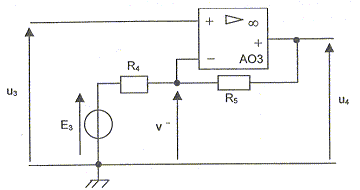
La tension u3 issue du filtre est appliquée à l'entrée du montage représentéci-dessous :

  1. Sachant que le mode de fonctionnement du montage est linéaire, en déduire une relation simple entre les tensions u3 et v-.
  2. Montrer que la tension de sortie u4 dépend des tensions d'entrée u3 et E3 selon la relation : u4 = (R4+R5)u3 /R4- R5/R4 E3.
  3. Sachant que R4 = 1 kW, déterminer les valeurs à donner à R5 et E3 pour que l'expression précédente devienne : u4 = 4× u3 - 12.
Relation simple entre les tensions u3 et v- :

En régime linéaire les deux entrées de l'A.O sont au même potentiel ( e=0)

u3 = v-.

Tension de sortie u4 :

On note i l'intensité qui travers R4 et R5.

E3 = v-+R4 i soit i = (E3 -v-) /R4

v- = u4 + R5 i = u4 +R5 (E3 -v-) /R4

v- (1+R5 /R4 ) = u4 +R5 E3/R4

u4 =v- (1+R5 /R4 ) -R5 E3/R4 ; u4 =u3 (1+R5 /R4 ) -R5 E3/R4 .

 Valeurs à donner à R5 et E3 pour que l'expression précédente devienne : u4 = 4× u3 - 12 :

D'une part : 1+R5 /R4 = 4 ; R5 /R4 =3 ; R5 = 3 kW.

D'autre part : R5 E3/R4 = 12 ; 3E3 = 12 ; E3 = 4 V.

 

 

 
retour -menu