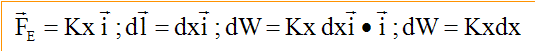Aurélie 25/06/07
 

système solide ressort, étude d'un enregistrement, aspect énergétique bac S Asie 2007

Google

Sans calculatrice, 5,5 points ; d'autres corrigés labolycée.org ; intellego.fr ; montblancsciences.free.fr.

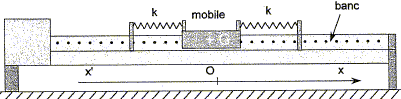
Au cours d'une séance de travaux pratiques, un groupe d'élèves étudie le mouvement d'un solide de masse m, posé sur un banc à coussin d'air horizontal et attaché à deux ressorts identiques de raideur k. Un capteur de position, non représenté, relié à un dispositif d'acquisition permet d'enregistrer la position du centre d'inertie G du mobile à chaque instant de date t. cette position est repérée sur un axe x'x horizontal, orienté de gauche à droite. L'origine O coïncide avec la position du centre d'inertie lorsque le mobile est à l'équilibre.

Etude d'un enregistrement :

 Les élèves réalisent un prmier enregistrement d'une durée de 2 s environ, en écartant le mobile de sa position d'équilibre.

  1. Le mobile est-il écarté de sa position d'équilibre vers la droite ou vers la gauche ? Justifier.
  2. Le mobile est-il lâché avec vitesse initiale ou sans vitesse initiale ? Justifier.
  3. Déterminer la période du mouvement en expliquant la méthode.
  4. Représenter sur la figure l'allure de la courbe qu'obtiendrait le groupe d'élèves si le mobile avait été lancé avec vitesse initiale depuis sa position d'équilibre dans le sens des x négatifs, l'amplitude du mouvement restant la même.
  5. Décrire une méthode analytique permettant d'obtenir une valeur approchée de la vitesse du mobile à un instant de date t1. ( aucun calcul n'est demandé).
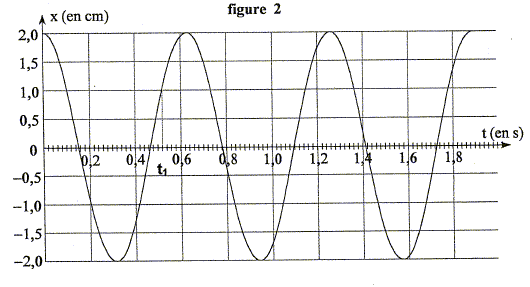
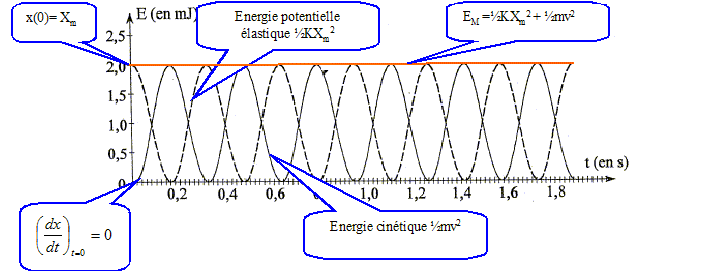
Le mobile est écarté de sa position d'équilibre vers la droite : à t=0, l'abscisse x(0)= 2,0 cm, valeur positive ( l'axe est orienté de la gauche vers la droite).

Le mobile est lâché sans vitesse initiale :

La tangente à la courbe à l'instant de date t=0, est horizontale : son coefficient directeur est donc nul.

Ce coefficient directeur de la tangente en x=0 s'exprime par [dx/dt]t=0.

[dx/dt]t=0 représente la vitesse initiale.

La période, notée T, exprimée en seconde, est la durée séparant deux passages successifs du mobile au même endroit et dans le même sens.

T= 0,63 s.

Méthode analytique permettant d'obtenir une valeur approchée de la vitesse du mobile à un instant de date t1.

Tracer la tangente à la courbe x(t) = f(t) à la date t1;

Déterminer le coefficient directeur de la tangente.
Etude théorique du mouvement :

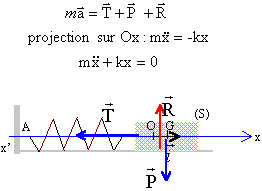
Le dispositif précédent peut être modélisé par un solide de masse m fixé à l'extrémité d'un seul ressort à spires non jointives, de masse négligeable et de raideur K= 2k. le solide glisse sans frottement sur un rail horizontal. Le mouvement du solide est étudié dans le référenciel terrestre considéré galiléen pendant la durée de l'expérience.

  1. Faire l'inventaire des forces qui s'exercent sur le solide et les représenter sans souci d'échelle mais de façon cohérente.
  2. En utilisant la deuxième loi de Newton, montrer que l'équation différentielle du mouvement du centre d'inertie G du solide se met sous la forme d2x/dt2 + K/m x=0.
  3. Cette équation diférentielle admet pour solution x(t) = Xm cos ( 2pt/T0+j) dans laquelle Xm et j sont des constantes qui dépendent des conditions initiales.
    - Déterminer Xm et j correspondant à la figure ci-dessus.
  4. Donner l'expression de la période T0 en fonction de K et m.
  5. Vérifier que l'enregistrement des élèves a été réalisé avec un mobile de masse m = 100 g et deux ressorts de raideur k =5,0 N /m. ( On prendra 2p = 6,3 rad )
Le mobile et soumis à son poids P, verticale vers le bas, valeur mg, à l'action du rail R , opposée au poids et à une force T qui rappelle le mobile vers sa position d'équilibre, dirigée vers la position d'équilibreO, de valeur proportionnelle à la déformation du ressort.


Déterminons Xm et j :

A t=0, l'abscisse x(0) vaut 2,0 cm ou 2,0 10-2 m.

2,0 10-2 = Xm cos j (1) avec Xm amplitude positive.

A t = 0, la vitesse est nulle : dx/dt = -Xm 2p sin ( 2pt/T0+j)

[dx/dt)t=0 = 0 = -Xm 2p/T0 sin j (2)

(2) conduit à sin j=0 soit j =0 ou j =p.

(1) conduit à Xm = 2,0 10-2 m et j=0.

Expression de la période T0 en fonction de K et m :

T0 = 2p(m/K]½.

Calcul de la masse m :

m = KT02 / (4p2 ) avec K = 2k = 10 N/m ; T0 = 0,63 s et 2p =6,3 rad soit T0 /(2p) = 0,63/6,3 = 0,1

m = K (2p / T0)2 = 10*0,12 = 0,1 kg = 100 g.

 

Etude énergétique :

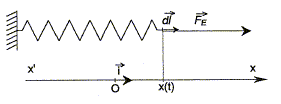
Quand un élève déplace le centre d'inertie du mobile de la position x=0 à la position x=Xm, il effectue un travail et fournit au système de l'énergie potentielle élastique.

  1. Donner l'expression du travail élémentaire dW de la force ( notée vecteur FE) exercé par l'élève au cours du déplacement élémentaire noté vecteur dl.
    Sur le schéma ci-dessous, pour plus de clarté, le mobile n'este pas représenté.

  2. Montrer que dans ce cas le travail élémentaire se met sous la forme dW=Kxdx
  3. Par une méthode analytique ou graphique, vérifier que le système acquiert au cours du déplacement, une énergie potentielle élastique EPE = ½KXm2.
  4. Pourquoi ne peut-on pas utiliser dans ce cas l'expression ?
  5. La figure ci-dessous représente les évolutions en fonction du temps de l'énergie cinétique et de l'énergie potentielle élastique.

    - Identifier les deux courbes en justifiant.
    - Tracer sur la figure la courbe représentant l'évolution en fonction du temps de l'énergie mécanique EM du dispositif solide-ressort en justifiant.
    - Pour un enregistrement de courte durée, l'énergie mécanique semble constante. Est-ce le cas réellement ? Pourquoi ?

Expression du travail élémentaire dW :

La force exercée par l'élève est opposée à la force qui rappelle le ressort vers sa position d'équilibre :

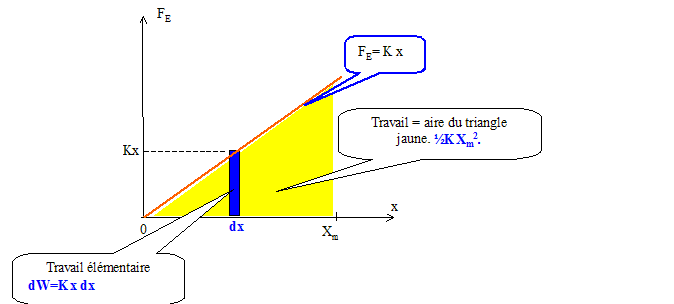
Puis intégration entre les valeurs 0 et Xm ; une primitive de x est ½x2.

W = [½x2]0Xm = ½KXm2.

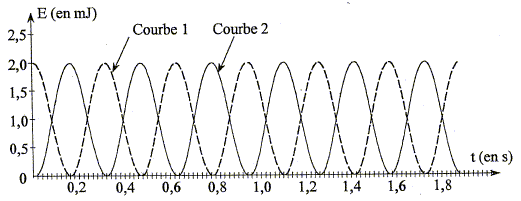
L'expression est utilisable si la force est constante, ce qui n'est pas le cas ici : la force de rappel dépend de x ( F= Kx).

Identifions les deux courbes :

Pour un enregistrement de courte durée, l'énergie mécanique semble constante. Dans la réalité il existe des forces de frottements. L'énergie mécanique va diminuer : une partie de celle-ci se dissipe sous forme de chaleur.
 
retour -menu