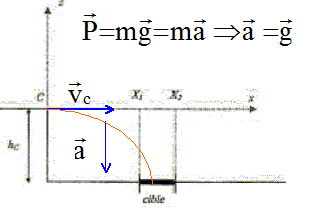Aurélie 26/06/07
 

Etude du mouvement d'un boulet sur un plan incliné, chute libre bacS 2007 Antilles

Google

4 points ; d'autres corrigés labolycée.org ; intellego.fr ; montblancsciences.free.fr.

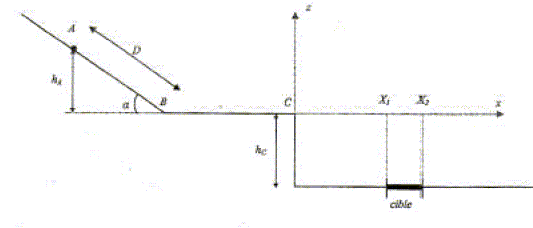
Le jeu schématisé ci-dessous consiste à placer un boulet sur un plan incliné de telle façon qu'il atteigne la cible.

Le boulet est tout d'abord laché en A sans vitesse initiale. Le système étudié est le boulet assimilé à un point. Toute l'étude est dans un référentiel galiléen. On néglige les frottements.

a= 30° ; D=AB=0,50 m ; L=BC=0,20 m ; hC= 0,40 m ; m= 10 g ; g=9,8m/s2.

 

Etude du mouvement du boulet entre A et B :

  1. Le système étudié est le boulet une fois lâché en A. Faire l'inventaire des forces extérieures agissant sur le boulet. Représenter ces forces sur un schéma sans soucis d'échelle.
  2. On choisit l'altitude du point C comme référence pour l'énergie potentielle de pesanteur Epp=0 pour zC=0.
    - Donner l'expression de l'énergie potentielle de pesanteur au point A et vérifier qu'elle vaut Epp(A) = 2,5 10-2 J.
    - En déduire l'expression puis la valeur de l'énergie mécanique du système au point A.
    - En déduire la valeur de l'énergie mécanique au point B. Justifier.
  3. Montrer que l'expression de la vitesse au point B est vB= (2gD sin a)½.
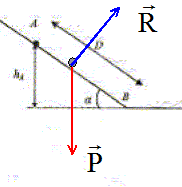
Inventaire des forces extérieures agissant sur le boulet :

Le poids, vertical, vers le bas, valeur mg.

L'action du plan, perpendiculaire au plan en absence de frottement.

Expression de l'énergie potentielle de pesanteur au point A :

Epp(A) = mg hA = mgD sin a avec m = 0,010 kg ; g = 9,8 m/s²; hA= D sin a = 0,50 sin 30 = 0,25 m.

Epp(A) = 0,010*9,8*0,25 ; Epp(A) = 2,5 10-2 J.

Expression puis la valeur de l'énergie mécanique du système au point A :

La vitesse, et en conséquence l''énergie cinétique sont nulles en A.

L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique :

EM(A) = Epp(A) = mgD sin a = 2,5 10-2 J.

Valeur de l'énergie mécanique au point B :

Entre A et B seul le poids travaille ( l'action du plan, perpendiculaire à la vitesse, ne travaille pas) : en conséquence l'énergie mécanique est constante entre A et B.

EM(B) = EM(A) = mgD sin a = 2,5 10-2 J.

Expression de la vitesse au point B :

L'altitude de B est égale à celle de C : zB=0 ; donc l'énergie potentielle de pesanteur est nulle en B.

En conséquence l'énergie mécanique du système est sous forme cinétique en B.

EM(B) = ½mvB2.

De plus EM(B) = EM(A) = mgD sin a

d'où : ½mvB2 =mgD sin a ; vB= (2gD sin a)½.

 
Etude de la chute du boulet après le point C :

On étudie le mouvement du centre d'inertie G du boulet après le point C. L'origine des temps est prise lorsque le boulet est en C. Le mouvement étant rectiligne et uniforme entre B et C, la vitesse en C est la même qu'en B : vC=vB=2,2 m/s.

  1. On précise que l'action de l'air est négligée.
    - Enoncer la deuxième loi de Newton.
    - Appliquer cette loi au boulet lorsqu'il a quité le point C.
    - Déterminer les composantes du vecteur accélération dans le repère Cxz.
  2. Déterminer les composantes du vecteur vitesse dans le repère Cxz.
    -L'expression des composantes du vecteur position dans le repère Cxz est :
    x= (2gD sin    a)½ t ; z= - ½gt2.
    - En déduire l'équation de la trajectoire donnant l'expression de z en fonction de x.
  3. On veut déterminer si le boulet atteint la cible E dont l'abscisse est comprise entre x1 =0,55 m et x2 = 0,60 m.
    - Calculer le temps nécessaire pour que le boulet atteigne le sol.
    - En déduire l'abscisse xS du boulet lorsqu'il touche le sol.
  4. Quelle distance D faudrait-il choisir pour atteindre le point de la cible à l'abscisse xS= 0,57 m ? ( la durée de la chute étant la même)
 

Enoncé de la deuxième loi de Newton :

 Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un système est égale au produit de la masse du système par la vitesse de son centre d'inertie G.

Lorsque que le boulet a quitté le point C, il se trouve en chute libre : il n'est soumis qu'à son poids.

Composantes du vecteur position dans le repère Cxz : ax=0 ; az=-g.

Composantes du vecteur vitesse dans le repère Cxz :

vitesse en C : vCx = vC =vB= (2gD sin a)½ ; vCz= 0

Le vecteur vitesse est une primitive du vecteur accélération :

vx= vCx = (2gD sin a)½ ; vy= -gt.

Equation de la trajectoire donnant l'expression de z en fonction de x :

x= (2gD sina)½ t donne t = x/(2gD sina)½

repport dans l'expression donnant z : z= - ½gt2.

z = -½g x2/(2gD sina).

Temps nécessaire pour que le boulet atteigne le sol :

Au sol z = - hC=- 0,40 m

- hC = - ½gt2 ; t = (2hC/g)½ = (2*0,40/9,8)½ ; t = 0,29 s. ( 0,286 s)
Abscisse xS du boulet lorsqu'il touche le sol :

xS= vC t = 2,2*0,286 ; xS=0,63 m.

Or l'abscisse de la cible est comprise entre x1 =0,55 m et x2 = 0,60 m : la cible n'est pas atteinte.

Quelle distance D faudrait-il choisir pour atteindre le point de la cible à l'abscisse xS= 0,57 m ?

x= (2gD sina)½ t ; x2/t2 = 2gD sina ; D= x2/( t2 2g sina)

D= 0,572 / ( 0,2862*2*9,8*sin 30) ; D= 0,41 m.

 

 
retour -menu