Aurélie 15/06/07
 

Etude d'une pile argent plomb, dosage des ions argent bac S 2007 Afrique

 http://www.edulyautey.org/~physique/

Google

La pile étudiée et son fonctionnement

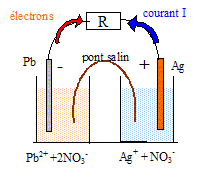
On introduit dans un bécher (1) un volume V1 =100,0 mL d'une solution de nitrate de plomb (Pb2+(aq) + 2NO3-(aq)) de concentration en soluté apporté cl = 0,100 mol/L dans laquelle plonge une lame de plomb.

Dans un second bécher (2), on verse un volume V2 = 100,0 mL d'une solution de nitrate d'argent ( Ag+(aq) +NO3-(aq)) de concentration en soluté apporté c2 = 0,100 mol/L dans laquelle plonge un fil d'argent.

On dispose également d'un pont salin.

On admet que la transformation chimique permettant à cette pile de fonctionner est décrite par la réaction:

2 Ag+(aq) + Pb(s) = 2 Ag(s)+Pb2+(aq).

La constante d'équilibre associée à cette réaction est K = 6,8 1028.

  1. Schématiser la pile que l'on peut construire avec ce matériel.
  2. Définir et calculer le quotient de réaction initial du système mis en jeu lors de la fabrication de la pile.
  3. Rappeler le critère d'évolution spontanée d'un système chimique.
  4. On branche une résistance aux bornes de la pile. En utilisant le critère d'évolution spontanée, indiquer en justifiant si la pile peut délivrer un courant électrique.
Après une heure d'utilisation :

La réaction se déroulant à l'électrode de plomb peut-être modélisée par : Pb = Pb2+ + 2e-.

La pile fonctionne pendant une heure en fournissant un courant d'intensité constante I= 65 mA.

Données : le faraday, valeur absolue de la charge d'une mole d'électrons 1 F = 9,65 104 C/mol ; nombre d'Avogadro : NA = 6,02 1023 mol-1.

Charge électrique élémentaire e = 1,6 10-19 C.

  1. Calculer la quantité d'électricité Q échangée pendant une heure d'utilisation.
  2. Calculer la quantité de matière d'électrons ne échangée pendant cette durée.
  3. Calculer la quantité de matière n(Pb2+) d'ions Pb2+(aq) formée pendant cette durée.
  4. Calculer la concentration finale en ions Pb2+(aq) notée [Pb2+(aq)] dans le bécher (1).

 

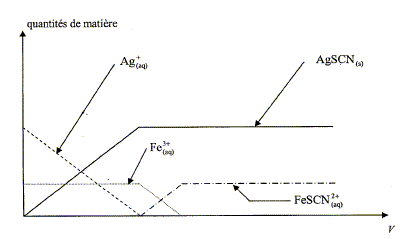
Quotient de réaction initial du système mis en jeu lors de la fabrication de la pile.

2 Ag+(aq) + Pb(s) = 2 Ag(s)+Pb2+(aq).

Q r i = [Pb2+(aq)]i /[Ag+(aq)]i2 =c1/c22 = 1/c2 = 1/0,100 ; Q r i = 10,0.

Le quotient initial Q r i est inférieur à la constante d'équilibre K : le système évolue spontanément dans le sens direct et la pile peut débiter un courant électrique.

La réaction se déroulant à l'électrode de plomb peut-être modélisée par : Pb = Pb2+ + 2e-. (1)

La pile fonctionne pendant une heure en fournissant un courant d'intensité constante I= 65 mA.

Quantité d'électricité Q échangée pendant une heure d'utilisation :

Q= I Dt avec I= 0,065 A et Dt= 3600 s.

Q = 0,065*3,6 102 = 234 C. ( 2,3 102 C)

Quantité de matière d'électrons ne échangée pendant cette durée.

Q= ne F ; ne = Q/F =234/ 9,65 104 ; ne = 2,4 10-3 mol.

Quantité de matière n(Pb2+) d'ions Pb2+(aq) formée pendant cette durée.

D'après les coefficients de (1) : n(Pb2+) = ½ne ; n(Pb2+) = 1,2 10-3 mol.

Concentration finale en ions Pb2+(aq) notée [Pb2+(aq)] dans le bécher (1).

Quantité de matière des ions Pb2+(aq) dans le bécher (1) = quantité de matière initiale + quantité de matière formée

n(Pb2+) totale = c1V1 + n(Pb2+) formé =0,1*0,1 +1,2 10-3 = 1,12 10-2 mol

[Pb2+(aq)] = n(Pb2+) /V1 = 1,12 10-2/ 0,100 = 1,1 10-1 mol/L.

Dosage des ions argent dans le bécher (2)

On désire maintenant déterminer la valeur de la concentration finale en ions Ag+(aq), notée [Ag+(aq)]f, en réalisant le dosage des ions Ag+(aq) présents dans le bécher (2).

Réflexions sur le protocole expérimental

On dispose d'une solution contenant des ions Ag+(aq) et des ions Fe3+(aq), on ajoute progressivement à ce mélange une solution contenant des ions thiocyanate SCN- (aq). Les réactions possibles sont les suivantes:

réaction (a) : Ag+(aq) +SCN- (aq) = AgSCN (s) ; le précipité formé est blanc.

réaction (b) : Fe3+(aq) + SCN- (aq) = FeSCN2+(aq) ; le composé formé est rouge sang.

Un logiciel permet de simuler les quantités de matière des espèces présentes dans la solution au fur et à mesure de l'ajout d'un volume V de solution de thiocyanate de potassium (K+(aq)) + SCN- (aq).

 

  1. Les réactions (a) et (b) ne se déroulent pas simultanément. Justifier cette affirmation en indiquant laquelle se déroule en premier.
    - Cette méthode permet de titrer les ions Ag+(aq). Indiquer comment est repérée l'équivalence de ce dosage.
    - Ce titrage est-il un titrage direct ou indirect des ions Ag+(aq) ? Justifier la réponse.
  2. Application aux ions Ag+(aq) contenus dans le hécher (2) après une heure d'utilisation de la pile.
    On prélève un volume Vp = 20,0 mL de la solution contenue dans le bécher (2) que l'on introduit dans un erlenmeyer. On ajoute à ce prélèvement 3,0 mL de solution de sulfate de fer(III) (2Fe3+(aq) +3S042-(aq) de concentration adaptée.
    Une solution de thiocyanate de potassium telle que [SCN-(aq)] = 2,0 10-1 moL/L, placée dans une burette, est progressivement ajoutée au contenu de l'erlenmeyer. L'équivalence est repérée lorsque le volume ajouté Veq = 7,5 mL.
    - Avec quelle verrerie faut-il prélever le volume Vp?
    - En déduire la valeur de [Ag+(aq)]f dans ce même bécher.
  3. L'équilibre chimique est-il atteint ?
    En utilisant les valeurs de [Pb2+(aq)]f et [Ag+(aq)]f, indiquer si l'équilibre chimique est atteint ou si la pile continue de fournir du courant.

 

Avant l'équivalence, le graphe montre :

- une diminution de la quantité de matière d'ion Ag+(aq)

- que la quantité de matière d'ion Fe3+(aq) reste constante.

Après l'équivalence, le graphe montre que :

- la quantité de matière d'ion Ag+(aq) est nulle

- la quantité de matière d'ion Fe3+(aq) diminue.

Les réactions (a) et (b) ne se déroulent pas simultanément : la réaction (a) se déroule en premier.

L'équivalence de ce dosage est repérée par l'apparition de la couleur rouge sang due à l'ion FeSCN2+(aq).

Ce titrage se déroule en une seule étape : c'est un titrage direct.

On prélève un volume Vp = 20,0 mL de la solution contenue dans le bécher (2) que l'on introduit dans un erlenmeyer. On ajoute à ce prélèvement 3,0 mL de solution de sulfate de fer(III) (2Fe3+(aq) +3S042-(aq) de concentration adaptée.
Une solution de thiocyanate de potassium telle que [SCN-(aq)] = 2,0 10-1 moL/L, placée dans une burette, est progressivement ajoutée au contenu de l'erlenmeyer. L'équivalence est repérée lorsque le volume ajouté Veq = 7,5 mL.
Le volume Vp, volume précis, est prélevé avec une pipette jaugée de 20,0 mL + pipeteur.
Valeur de [Ag+(aq)]f dans ce même bécher :

A l'équivalence les quantités de matière de réactifs mis en présence sont en proportions stoechiométriques :

Vp[Ag+(aq)]f = [SCN-(aq)] Veq.

[Ag+(aq)]f = [SCN-(aq)] Veq / Vp = 2,0 10-1 *7,5 / 20,0 =7,5 10-2 mol/L.

L'équilibre chimique est-il atteint ?

Q r f= [Pb2+(aq)]f /[Ag+(aq)]f2 =1,12 10-1/(7,5 10-2)2 ; Q r f =20.

Le quotient Q r f est inférieur à la constante d'équilibre K :
l'équilibre chimique n'est pas atteint et la pile peut continuer à fournir du courant.
 
retour -menu