Aurélie 14/06/07
 

Principe de l'allumage d'une voiture, batterie, dipole RL bac S 2007 Afrique

 http://www.edulyautey.org/~physique/

Google

La batterie : principe de fonctionnement

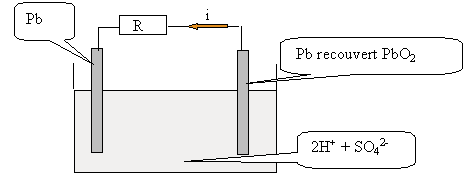
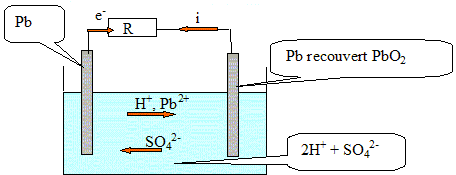
La batterie d'une voiture est un accumulateur au plomb constitué de deux électrodes en plomb Pb(s) dont l'une est recouverte de dioxyde de plomb Pb02(s). L'ensemble est immergé dans une solution concentrée d'acide sulfurique 2H+(aq) + SO42-(aq). Lorsque la voiture démarre, l'accumulateur fonctionne comme une pile.

  1. Par souci de simplification, on considérera que les couples mis en jeu sont Pb2+(aq)/Pb(s) et Pb02(s)/Pb2+(aq). Écrire les demi-équations électroniques associées à ces deux couples.
  2. L'accumulateur est schématisé ci-dessous. Flécher les sens de circulation des porteurs de charge dans les fils de connexion et dans la solution d'acide sulfurique.
  3. Justifier que l'équation de la réaction modélisant la transformation chimique qui a lieu lors du démarrage de la voiture peut s'écrire :
    Pb(s) + Pb02(s) +4H+(aq) = 2Pb2+(aq) + 2H20(I)
    Lorsque la voiture roule, la batterie se recharge et fonctionne comme un électrolyseur.
  4. Indiquer si la transformation chimique envisagée est spontanée ou forcée. En déduire le sens de circulation du courant électrique.
  5. Sachant que les mêmes couples oxydant / réducteur interviennent lors du démarrage de la voiture et lorsqu'elle roule, écrire l'équation de la réaction modélisant la transformation chimique qui a lieu lors de la recharge de la batterie.
Préciser pour chaque électrode la nature (oxydation ou réduction) de la réaction observée. Puis indiquer, sur le schéma, la cathode et l'anode.
Demi-équations électroniques associées à ces deux couples.

Pb(s) =Pb2+(aq) +2e- (1)

Pb02(s)+ 4H+ + 2e- = Pb2+(aq) +2H2O. (2)

L'oxydation du plomb libère des électrons : le plomb constitue une anode négative.

L'électrode recouverte de Pb02(s) est une cathode positive sur laquelle se produit une réduction ( gain d'électrons).

(1) + (2) donne : Pb(s) + Pb02(s) +4H+(aq) = 2Pb2+(aq) + 2H20(I)

électrolyseur

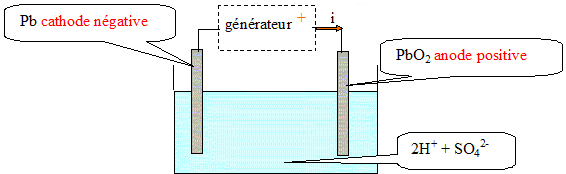
L'électrolyse est une transformation forcée qui nécessite un apport d'énergie sous forme électrique.

Le générateur impose le sens du courant de charge : la borne positive de la batterie doit être reliée à la borne positive du générateur.

A la cathode négative les ions Pb2+(aq) se réduisent en plomb suivant :

Pb2+(aq) +2e- = Pb(s) (3) réduction

A l'anode positive les ions Pb2+(aq) s'oxydent en Pb02(s) suivant :

Pb2+(aq) +2H2O = Pb02(s)+ 4H+ + 2e- (4) oxydation

(3) + (4) donne : 2Pb2+(aq) + 2H20(I) = Pb(s) + Pb02(s) +4H+(aq)
Étude de l'allumage de la voiture

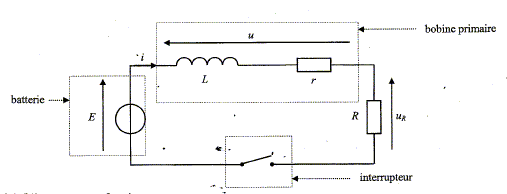
Pour permettre l'allumage des bougies d'une voiture, une étincelle est créée au niveau des bougies. La formation de cette étincelle est liée à l'ouverture, puis à la fermeture d'un circuit comprenant notamment une bobine. Un courant électrique circule dans un circuit comprenant la batterie de la voiture, la bobine appelée bobine

primaire et un interrupteur électronique. On considérera que la batterie de la voiture délivre une tension continue qui vaut E = 12 V.

La bobine primaire est caractérisée par une inductance L et une résistance interne r = 0,50 W.

Le schéma simplifié du principe est donné ci-dessous où R représente la résistance des autres éléments du circuit. On prendra R = 2,5W.

A t = 0, le courant ne circule pas dans le circuit, puis l'interrupteur est fermé.

  1. Donner l'expression de la tension u aux bornes de la bobine primaire en fonction de r, L et i.
  2. Montrer que l'équation différentielle régissant l'évolution de i est: : L di/dt +Ki = E où K est une constante dont on donnera l'expression en fonction des paramètres du circuit.
  3. Une solution de l'équation différentielle peut s'écrire i =A (1- exp(-Bt)) où A et B sont deux constantes positives non nulles. En utilisant l'équation différentielle, montrer que A = E/K et que B = K/L.
    - Calculer la valeur de A. Préciser son unité.
  4. Parmi les courbes 1, 2 et 3 données ci-dessous, indiquer, en justifiant, celle qui peut représenter i.


  5. Déterminer graphiquement la valeur de la constante de temps t du circuit à partir de la courbe choisie.
  6. Donner l'expression littérale de la constante de temps t en fonction des paramètres du circuit.
  7. En déduire la valeur de l'inductance L de la bobine primaire.
  8. Donner l'expression littérale de l'énergie WL emmagasinée dans la bobine primaire.
  9. Calculer l'énergie maximale emmagasinée dans la bobine primaire à l'aide de la courbe choisie.
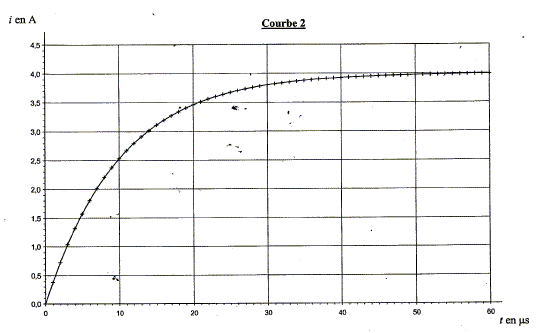
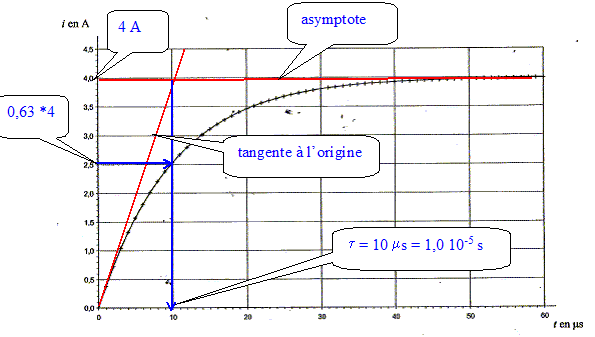
Expression de la tension u aux bornes de la bobine primaire en fonction de r, L et i.

u= Ldi/dt + ri.

Equation différentielle régissant l'évolution de i :

additivité des tensions : u + uR= E avec uR= Ri

d'où Ldi/dt + (R+r) i = E (1).

Expression de la forme Ldi/dt + K i= E avec K= R+r exprimée en ohm.

Une solution de l'équation différentielle peut s'écrire i =A (1- exp(-Bt)) où A et B sont deux constantes positives non nulles.

Dériver i(t) par rapport au temps : di/dt = ABexp(-Bt)

Repport dans (1) : ABLexp(-Bt) +AK-AKexp(-Bt) = E

Cette égalité est vérifiée quel que soit le temps si : BL=K soit B=K/L et si AK= E soit A= E/K.

Calcul de la valeur de A :

A = E/(R+r) avec E=12 V et R+r =3W.

A = 12/3 = 4 ampères.

La courbe 2 correspond à l'intensité i(t) =4 (1- exp(-Bt))

La courbe correspond à une fonction croissante de la valeur 0 à la valeur 4 A en accord avec l'expression de i(t) proposée.

Valeur de la constante de temps t :

Expression littérale de la constante de temps t = L/(R+r).

Valeur de l'inductance L de la bobine primaire :

L= t(R+r) = 1,0 10-5 *3 = 3,0 10-5 H.

Expression littérale de l'énergie WL emmagasinée dans la bobine primaire.

WL = ½LI2.

Energie maximale emmagasinée dans la bobine primaire :

WL = ½LI2 = 0,5 * 3,0 10-5 * 42 = 2,4 10-4 J.

 

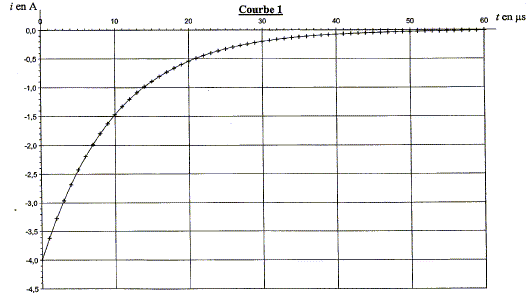
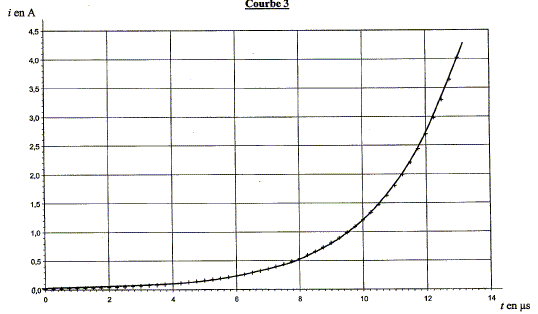
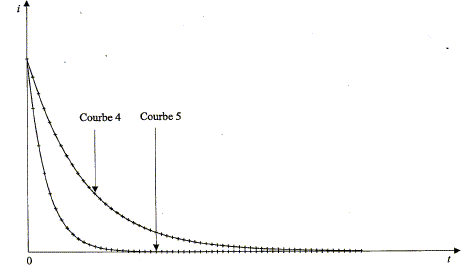
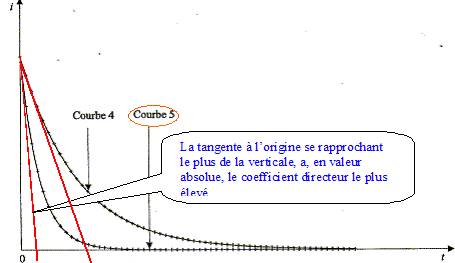
Étude de la formation de l'étincelle

Après la phase précédente, on modifie le circuit pour que l'intensité du courant diminue.

En modifiant les paramètres du circuit, on peut obtenir différentes allures de l'intensité du courant circulant dans la bobine. Deux courbes représentant l'allure de cette intensité sont proposées ci-dessous.

Le coefficient directeur de la tangente à l'origine est représenté par Di/Dt. A quelle courbe correspond la valeur de |Di/Dt| à t = 0 la plus élevée ?
 
retour -menu