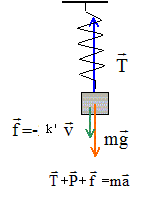|
|
Le sismographe se
compose d'une masse M relié a un ressort de raideur K de longueur au
repos l0. L'extremité du ressort est attaché en
un point fixe du référentiel Rl du laboratoire
que l'on suppose galiléen. On repère le mouvement du centre de masse M
du bloc par son élongation x(t) mesurée a partir de la position
d'équilibre de l'ensemble ressort + masse.
-
Schéma
les forces en présence
:
|
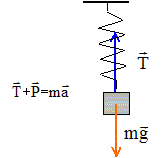
poids : vertical, vers le
bas, appliqué au centre d'inertie, valeur : mg
tension du ressort :
verticale, dirigée vers la position d'équilibre, appliquée au point de
fixation masse ressort, valeur proportionnelle à la déformation du
ressort.
|
-
Appliquer
le principe fondamental de la dynamique ( 2ème loi de Newton) pour
établir l'équation du mouvement :
écrire cette loi sur un axe vertical dirigé vers le bas ; l'origine de
l'axe est la position d'équilibre stable du système masse ressort :
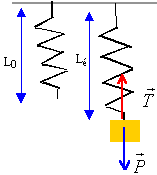
à l'équilibre : mg = k(Léq-L0)
|
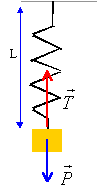
écarté de sa position d'équilibre le ressort
oscille : L= Léq +x
mg-k(L-l0)= m d²x/dt²
mg-k( Léq +x-l0)=
m d²x/dt²
mg-k( Léq -l0)
- kx =m d²x/dt² ; or mg = k(Léq-L0)
m
d²x/dt² + k x=0 (1)
|
-
Pulsation w0
( rad s-1) :
w0 = [k/m]½
d'où l'écriture de (1) : d²x/dt² + w20 x = 0 ou x" +w20 x
=0. (1)
-
La
solution de cette équation peut se mettre sous la forme x(t)=A cos(Bt) ou A et B sont des
constantes positives non nulles :
Calcul de B pour que x(t)=AcosBt soit solution de l'équation
différentielle.
dériver deux fois par rapport au temps :
x' = AB (-sin (Bt) ; x" = -AB2cos(Bt)
repport dans (2) : -AB2cos(Bt) + w20A cos(Bt)
=0 ; B=w0
On éloigne la masse de sa
position d'equilibre d'une quantité d, on a donc à t=0, x(0)=d ;
à partir de cette condition initiale,on détermine la constante A en
fonction des données du problème.
x(t=0)=A cos(0) = d soit A=d.
Le mouvement de la masse est un mouvement rectiligne sinusoïdal, sans
amortissement.
-
On considere
que le mouvement est amorti
par un frottement visqueux de coefficient f. On précise alors que la
force de frottement visqueux est proportionelle à la vitesse.
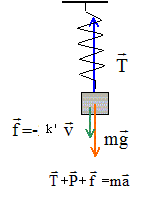
|
écrire
cette loi sur un axe vertical dirigé vers le bas ; l'origine de l'axe
est la position d'équilibre stable du système masse ressort :
L= Léq +x
mg-k(L-l0)-2lv= m d²x/dt²
mg-k( Léq +x-l0)-k'v=
m d²x/dt²
mg-k( Léq -l0)
- kx -k'v =m d²x/dt² ; or mg = k(Léq-L0)
m d²x/dt² +k'v + k x=0 avec v = dx/dt = x'
m
d²x/dt² +k'x' + k x=0 (3)
|
(3 ) peut s'écrire : d²x/dt² +k'/ m x' + k/ m x=0
or w20 = k/m ; on pose 2l= k'/m ;
d'où : d²x/dt²
+2l x' + w20 x=0 (4)
Dimension de l :
d²x/dt² a la
dimension d'une accélération (m/s²) ou bien : [d²x/dt²]= L T-2.
chaque terme de la somme de l'équation (4) a donc la dimension d'une
accélération
de plus x' ou dx/dt a la diension d'une vitesse ( m/s) soit [x']=L T-1.
[2lx'] = L T-2 ; [x']=L T-1
; d'où [l] = T-1 ( inverse d'un temps)
-
En
fonction du signe du discriminant D les solutions de cette équation sont :
x" +2l x' + w20 x=0
équation caractéristique associée : r²+2lr+ w20 =0
D=4(l2-
w20 )
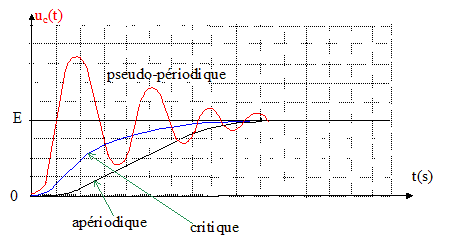
si D <0 : pulsation w² = w0²
-l²
solution : x = B exp( -lt) sin (wt+j), régime pseudopériodique (
amortissement faible)
si D =0 : r = -l
; solution : x = (At+B )exp( -lt) ; régime critique.
si D >0 : r1
= -l+ w ; r2
= -l- w ;
solution : x = C1
exp( r1 t)
+ C2 exp( r2
t) ; régime apériodique.
-
Vérifions
que x(t) est solution de l'équation différentielle : ( si D>0)
dériver par rapport au temps x'(t) = C1 r1exp( r1 t) +
C2 r2
exp( r2
t)
dérivée seconde : x"= C1 r21exp(
r1 t)
+ C2 r22
exp( r2
t)
repport dans x" +2l x' + w20 x=0
C1 r21exp(
r1 t)
+ C2 r22
exp( r2
t)+2l[C1
r1exp(
r1 t)
+ C2 r2
exp( r2
t)]+
w20[C1
exp( r1 t)
+ C2 exp( r2
t)]=0
[ r21+2lr1
+ w20 ]C1exp(
r1 t)
+ [ r22+2lr2
+ w20 ]C2exp(
r2 t)
=0 (5)
Or [ r21+2lr1
+ w20 ] = [
r22+2lr2
+ w20 ] =0
(5) est donc bien vérifiée quel que soit t : x = C1
exp( r1 t)
+ C2 exp( r2
t) est bien solution de (4)
|