Pendule cycloïdal : oscillateur harmonique

Aurélie 3/3/06

Les frottements sont négligés. Le petit solide de masse m se déplace sur l'arc de cycloïde dont les éqations paramètriques sont : x= a(q+sinq) et y=a(1-cosq). a est une constante et q varie de -p à + p.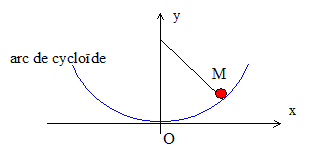

Exprimer la longueur d'un déplacement élémentaire ds en fonction de a, q et dq puis l'abscisse curviligne OM = s en fonction de a et q.
Exprimer l'énergie mécanique du mobile en fonction de s et s'.
Etablir l'équation différentielle relative à s en dérivant par rapport au temps l'expression précédente. En déduire la période T du mouvement.
A l'instant initial t=0, q =q_M ( position M₀) la vitesse initiale est nulle. Quelle est la vitesse de passage en O ? Quelle est la durée du parcours M₀O ?

corrigé

déplacement élémentaire ds = racine carrée (dx²+dy²)

x= a(q+sinq) d'où dx = a(1+cosq)dq ; y=a(1-cosq) d'où dy =a sinq dq ;

ds² =a²[(1+cosq)²+ sin²q )dq ² = a²(2+2cosq )dq ² =2a²(1+cosq)dq ² =4a² cos² (½q)dq ²

ds = 2a cos (½q)dq .

longueur de l'arc OM: intégrer entre 0 et q. (primitive de cos (½q) : 2 sin (½q) )

énergie mécanique = énergie potentielle + énergie cinétique

Le solide de masse m est soumis à son poids et à la tension du fil ( celle-ci ne travaille pas, elle est perpendiculaire à la vitesse)

énergie potentielle E_p= mgy avec y altitude de M

E_p= mga(1-cosq) = 2mg a sin²(½q) = 2mga [s/(4a)]² = mg s²/(8a)

énergie cinétique Ec= ½ms'² ; énergie mécanique E= ½ms'² +mg s²/(8a).

équation différentielle :

l'énergie mécanique est constante ( seul le poids travaille) dE/dt = 0

0 = m s" s'+ mg s s'/(4a) ; 0= s"+g/(4a) s.

équation différentielle d'un oscillateur harmonique de pulsation w telle que w² = g/(4a)

période T= 2p/w = 4p [a/g]^½, valeur indépendante de l'amplitude q_M.

vitesse de passage en O : date de ce premier passage en O : t = 0,25 T = p [a/g]^½

l'énergie mécanique initiale est sous forme potentielle : 2mg a sin²(½q_M)

l'énergie mécanique finale est sous forme cinétique ( O : origine de l'énergie potentielle) : ½mv²

l'énergie mécanique se conserve : ½mv² = 2mg a sin²(½q_M)

v² = 4g a sin²(½q_M)

retour -menu