champ magnétique crée dans le stator d'un moteur électrique

magnétostatique

http://perso.orange.fr/jeanmarc.drocourt/elec/Masta.pdf

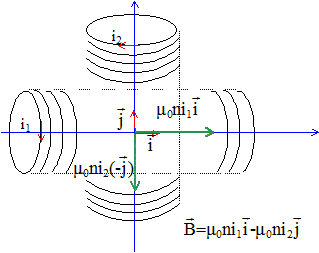
 I- Champ magnétique crée dans le stator ( partie fixe)

Les deux solénoïdes infinis, identiques, disposés dans le vide, ci-dessous sont perpendiculaires ( rayon R, et n spires par unité de longueur) . Un courant d'intensité i₁(t)=I_m cos(wt) parcourt le solénoïde horizontal. Un courant d'intensité i₂(t)=I_m cos(wt+½p) parcourt le solénoïde vertical. Chaque bobine est constituées de 5 couches de spires jointives. Le fil est cylindrique de diamètre d=2a= 0,2 mm. I_m = 20 A. m₀ = 4 p 10^-7 H m^-1.

Champ magnétique crée à l'intersection des axes :

or i₂(t)=I_m cos(wt+½p) = - sin (wt) d'où :

valeur de B au centre : B²= (m₀ nI_m)² ( cos²(wt) + sin²(wt)) = (m₀ nI_m)² ;

B= m₀ nI_m , valeur constante, le champ magnétique est uniforme dans la partie centrale.

angle formé entre le champ magnétique et l'axe horizontal : tan a = sin (wt) / cos (wt) = tan (wt ) ; a = wt.

calcul de n : nombre de spires par mètre

Dans une couche il y a : N= L/(2a) conducteurs; dans 5 couches, il y a : 5N= 5L/(2a) conducteurs

d'où n=5N/L= 5 / (2a) =5/(2 10^-4) =2,5 10⁴ spires par mètre.

B= 4*3,14 10^-7*2,5 10⁴*20 =0,63 T.

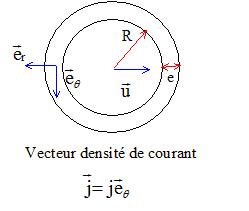
On considère le solénoïde horizontal seul ( vue en coupe ci-dessous). On asimile les courants filiformes à une distibution volumique uniforme de courant. R= 5 cm ; e = 10 a = 0,001 m.

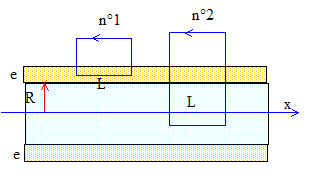
La densité de courant est définie comme le courant électrique par unité de surface.

J= i₁/(4a²) ; J_max = I_m/ (4a²) = 20 / 4*(10^-4)² = 5 10⁸ A m^-2.

Champ magnétique à la distance r de l'axe en fonction de J, R, e, m₀ et r :

un plan perpendiculaire à l'axe du solénoïde est plan de symétrie pour le courant : ce plan est un plan d'antisymétrie pour le champ magnétique. Le champ magnétique est donc parallèle à Ox.

De plus , par rotation autour de l'axe Ox et par translation parallèle à Ox, la distribution de courant ne change pas. Donc le champ magnétique ne dépend que de r, distance du point M à l'axe Ox.

Enfin le champ magnétique est nul à l'extérieur du solénoïde infini.

Appliquer le thèorème d'Ampère aux rectangles 1 et 2 ci-dessous :

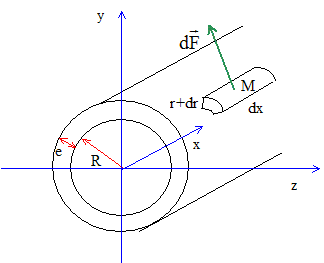
rectangle n°1 : si R< r <R+e : B_s L=m₀J(R+e-r) L d'où B_s = m₀J(R+e-r)

rectangle n° 2 : r <R : B_s L=m₀J e L d'où B_s = m₀J e

Force élémentaire de Laplace s'exerçant sur un élément de volume dt= rdr dq dx entourant le point M.

Force de Laplace :

élément de volume : dt= rdr dq dx = dr dS ; B= m₀J(R+e-r)

dF= JBdt = m₀J²(R+e-r)dr dS ; dF/dS= m₀J²(R+e-r)dr

intégrer entre R et R+e pour obtenir la densité superficielle de force s'exerçant sur la surface dS= rdq dx

changement de variable y = R+e-r ; dy = -dr ; intégrer entre e et 0 :

d'où : -m₀J²½ [y²]_e⁰ = ½m₀J²e².

A.N : valeur maximale : 0,5 * 4*3,14 10^-7*(5 10⁸)² *(10^-3)² = 1,5 10⁵ Pa.

valeur très importante : l'enroulement devrait être très solide. De plus, variant au cours du temps, elle va engendrer des vibrations.

Pratiquement le champ magnétique du stator est crée par des électroaimants : en associant bobinage et noyau de fer, on peut obtenir des champs magnétiques assez grands. ( de l'ordre du tesla)