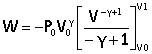A. Dans une carabine à air comprimé, une masse d'air (assimilée à un gaz parfait) telle que g=1,4, ocupe un volume V= 5 cm³ sous la pression P₀ =10⁶ Pa, à la température de 15°C. Cette masse d'air se détend adiabatiquement dans le canon de longueur L=1 m et de section s= 0,25 cm², en propulsant le projectile de masse m= 1g, dans l'atmosphère.

1. Calculer la pression P₁ de la masse d'air à la fin de la détente.
2. Calculer la température de la masse d'air à la fin de la détente.
3. Calculer le travail W fourni par la masse d'air au cours de la détente.
4. En supposant que ce travail est intégralement cédé à la balle pour la propulser, quel est le module de la vitesse à la sortie du canon ?

B. En réalité v₀ = 90 m/s. Un enfant envisage de chasser un moineau avec cette carabine. On se propose d'étudier la trajectoire du projectile.

Un moineau M est posé sur la cime d'un arbre à une hauteur h= 6,30 m. Lorsque l'enfant épaule l'extrémité C du canon se situe à H= 1,30 m du sol. L'arbre est distant de L= 15 m de l'extrémité du canon. On néglige la résistance de l'air.

1. Pour le premier tir, suite à un mauvais réglage du système de visée, l'axe du canon est dirigé sur le moineau. Le coup part et la balle perce une feuille située en un point I au dessous du moineau M. Exprimer puis calculer MI.
2. Le moineau est resté posé au même endroit. L'enfant règle le système de visée. On demande de trouver l'angle b que doit avoir l'axe du canon avec l'horizontale poutr que le moineau soit atteint. Calculer l'écart entre a et b et conclure. g=9,81 m/s².

---

---

corrigé

---

pression P₁ de la masse d'air à la fin de la détente : P₀V^g= P₁V₁^g soit P₁ = P₀(V/V₁)^g

avec V₁= Ls = 100*0,25 = 25 cm³ ; P₁ =10⁶ (5/25)^1,4 = 1,05 10⁵ Pa.

température de la masse d'air à la fin de la détente : P₁V₁= nRT₁ avec n= P₀V/(RT₀)

T₁ = P₁/P₀ V₁/V T₀ = 0,105 * 5*(273+15) = 151,2 K.

travail W fourni par la masse d'air au cours de la détente :

dW= - PdV et P = P₀V₀^g /V ^g.

dW=-P₀V₀^g dV/V ^g. On intègre :

W = 10⁶ (5 10^-6)^1,4 / 0,4 [(25 10^-6])^-0,4-(5 10^-6)^-0,4] = -5,93 J.

Vitesse à la sortie du canon : la balle emporte ce travail sous forme d'énergie cinétique ½mv²

d'où v² = 2W/m = 2*5,93 / 10^-3 = 11863 ; v = 109 m/s.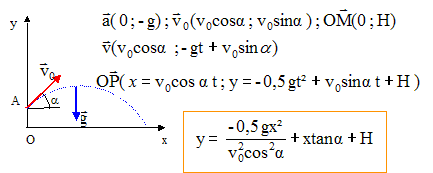

---

Calcul de y pour x=L=15 m ; v₀ = 90 m/s ; tan a = (h-H) / L = 5/15 = 0,333 soit a = 18,43° ; cos a =0,9486 ; H= 1,30 m

y = -0,5*9,81*15² / (90*0,9486)² +15*0,3333 +1,30 = 6,148 m soit MI= 0,152 m.

angle b : dans l'expression précédente , l'inconnue est cos b avec y= 6,30 m

y-H = 5 m ; -0,5gL²/v₀² = -0,5*9,81*15²/90² =-0,136 ; 1+ tan² b = 1/cos²b

d'où : 5 = -0,1362 (1+ tan² b)+ 15 tan b ; on pose X= tan b

-5 -0,136 (1+ X²)+ 15X=0 soit -0,136X² + 15X-5,136 =0

X=0,343 soit b= tan^-1 0,343 = 18,93°.

La différence entre a et b est voisine de 0,5°.

---