|
CAPES physique chimie ( d'après concours interne 2005 ) Détente d'un gaz : énergie interne et entropie |
||||
|
||||
|
On considère deux réservoirs identiques aux parois rigides et parfaitement calorifugées. Ils communiquent par un tube à robinet. On note V0 = 12 L le volume d'un des réservoirs. A l'état initial le compartiment noté A contient une mole de gaz parfait monoatomique à la température T0 = 300 K et le compartiment B est vide. La pression initiale est notée P0. On ouvre le robinet et le gaz se répartit dans les deux réservoirs et atteint un nouvel équilibre thermodynamique. On note Tf1 la température finale et Pf1 la pression finale.
On considère maintenant une mole de ce même gaz monoatomique enfermé dans un cylindre vertical, muni d'un piston de masse négligeable et coullssant sans frottement. Les parois du cylindre et du piston sont diathermes ( perméables à la chaleur). L'ensemble du système se trouve au contact d'un thermostat à T0 = 300 K. Le volume initial du gaz est égal à V0 = 12 L et sa pression initiale est égale à P0. Le piston est initialement bloqué par l'opérateur. La pression de l'atmosphère extérieure est maintenue à ½P0 pendant toute l'expérience. 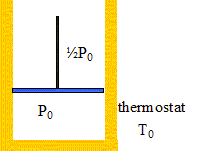
Energie interne : La somme des énergies microscopiques ( cinétique et
potentielle) constitue l'énergie interne d'un système. Dans toute transformation l'énergie se conserve. La variation de l'énergie interne d'un système fermé est égale à l'énergie échangée avec l'extérieur, sous forme de chaleur et sous forme de travail . DU= W+Q Système adiabatique : le transfert thermique Q1 est donc nul. Système indéformable : le travail des forces de pression W1 est nul en conséquence DU1 = 0 ; l'énergie interne est constante. Gaz parfait monoatomique : Les espèces constituants le gaz sont des atomes ;
l'énergie interne est sous forme d'énergie cinétique des molécules . dérivée partielle par rapport à la température de l'énergie interne, à volume constant. - Expressions et calculs de P0, Tf1 et Pf1 en fonction des données : DU1 =Cv m (Tf1-T0) = 0 d'où Tf1=T0 loi des gaz parfaits : P0V0=Pf1 *2V0 = RT0 soit Pf1 = ½P0 = RT0 / (2V0)= 8,31*300/ (12*2 10-3) = 1,03 105 Pa. Expression et calcul de la variation d'entropie DS1 du gaz lors de cette détente : L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. imaginer une transformation réversible passant de l'état initial à l'état final transformation élémentaire : dS =dQ/T= (dU-dW)/T = Cv, m /T dT+ PdV/T = R/(g-1) /T dT+ RdV/V intégrer entre T0 et Tf1 : DS1 =Cv, m ln(Tf1 /T0) + Rln(Vf 1/V0) = R ln 2= 5,8 J K-1. Bilan entropique : entropie échangée Se1 = Q/T0 = 0 entropie créee Sc1 = DS1 - Se1 =5,8 J K-1. L'opérateur lâche brutalement le piston : détente brutale irréversible. Evolution monotherme, irréversible : la pression du gaz n'est bien définie que lorsque le nouvel équilibre est atteint ( état final). L'état final Tf2, Pf2, Vf2 : A l'équilibre mécanique, les pressions intérieure et extérieure sont égales : Pf2 = ½P0 et la température finale est égale à celle du thermostat Tf2 = T0. Le travail mécanique des forces pressantes extérieures à pression constante vaut : W2= -½P0(Vf2-V0) équation du gaz parfait : P0V0/T0= ½P0Vf2/Tf2 ; V0/T0= ½Vf2/T0 ; soit : Vf2 = 2V0. d'où W2= -½P0(Vf2-V0) = -½P0V0= -½RT0 = -0,5*8,31*300 = -1,25 kJ. Conservation de l'énergie ( premier principe ) DU2= W2+Q2 et DU2= Cv,m(Tf2-T0) =0 Q2 = - W2 = 1,25 kJ. Expression et calcul de la variation d'entropie DS2 du gaz lors de cette détente : L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. imaginer une transformation réversible passant de l'état initial à l'état final transformation élémentaire : dS =dQ/T= (dU-dW)/T = Cv, m /T dT+ PdV/T = R/(g-1) /T dT+ RdV/P intégrer entre T0 et Tf2 : DS2 =Cv, m ln(Tf2 /T0) + Rln(Vf 2/V0) = R ln 2= 5,8 J K-1. Bilan entropique : entropie échangée Se2 = Q2/T0 = 1,25 103 / 300 = 4,16 J K-1. entropie créee Sc2 = DS2 - Se2 =5,8 -4,16 = 1,6 J K-1.
A l'équilibre mécanique, les pressions intérieure et extérieure sont égales : Pf3 = ½P0 et la température finale est égale à celle du thermostat Tf3 = T0. Conservation de l'énergie ( premier principe ) DU3= W3+Q3 et DU3= Cv,m(Tf3-T0) =0 dW3 = -PdV = -RT0/VdV = -RT0d(ln V) W3 = -RT0ln(2V0/V0) = -RT0 ln2 = -8,31*300*ln2 = -1,7 kJ. W3+Q3 = 0 soit Q3 = 1,7 kJ Expression et calcul de la variation d'entropie DS3 du gaz lors de cette détente : L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. imaginer une transformation réversible passant de l'état initial à l'état final transformation élémentaire : dS =dQ/T= (dU-dW)/T = Cv, m /T dT+ PdV/T = R/(g-1) /T dT+ RdV/P intégrer entre T0 et Tf3 : DS3 =Cv, m ln(Tf3 /T0) + Rln(Vf 3/V0) = R ln 2= 5,8 J K-1. Bilan entropique : entropie échangée Se3 = Q3/T0 = 1,7 103 / 300 = 5,8 J K-1. entropie créee Sc2 = DS2 - Se2 =5,8 -5,8 = 0 J K-1,
transformation réversible.
l'énergie interne, l'entropie sont des fonctions d'états. le travail des forces de pression, le transfert thermique, l'entropie céee et l'entropie échangée dépendent du type de transformations ; ce ne sont pas des fonctions d'état. |
||||
|
|