Aurélie 02/06
 

Complexes et précipitation ( concours Centrale 01 )

Les ions de l'aluminium

Google

Les ions de l'aluminium en solution aqueuse :

 

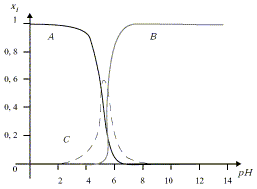
Al3+ + H2O = Al(OH)2+ + H+ ; Ka = 10–5

Al(OH)3(solide) = Al3+ + 3 OH– ; KS = 10–32

Al(OH)3(solide) + OH– = Al(OH)4– ; K= 103

On considère que l'aluminium en solution aqueuse se trouve sous l'une des formes suivantes : Al3+, Al(OH)2+ et Al(OH)4–.

On désigne par s la concentration totale de l'aluminium en solution aqueuse en présence du précipité d'hydroxyde d'aluminium et on pose :

x1 = [Al3+]/s ; x2 = [Al(OH)2+]/s ; x3 = [Al(OH)4–]/s

  1. Exprimer x1 , x2 et x3 en fonction de h = [H3O+] , Ka , K.s , K et Ke (produit ionique de l'eau égal à 10–14).
  2. Le graphe ci-dessous représente les variations des xi en fonction du pH. Identifier les différentes courbes. Justifier.
  3. On ajoute progressivement de la soude concentrée à une solution de chlorure d'aluminium de concentration c0 = 0,5 mol.L–1 (le volume de la solution peut être considéré comme constant)
    - Un précipité apparaît pour pH1 et disparaît pour pH2. Interpréter et calculer pH1 et pH2.
    - Déterminer la valeur pH3 pour laquelle la quantité de précipité est maximale.
    - Montrer que si c0 est inférieure à une limite sm que l'on calculera, il est impossible de former le précipité.

corrigé
s =[ Al3+] +[Al(OH)2+] + [Al(OH)4–]

Al3+ + H2O = Al(OH)2+ + H+ ; Ka =[Al(OH)2+ ] h / [Al3+] d'où : [Al(OH)2+ ]= Ka [Al3+] / h (1)

Al(OH)3(solide) = Al3+ + 3 OH– ; KS =[Al3+][OH–]3.

de plus Ke = [OH–] h d'où : [OH–] = Ke/h.

KS =[Al3+][OH–]3 = [Al3+] Ke3/ h3 d'où : [Al3+] = KSh3 / Ke3 (2)

(1) et (2) donnent : [Al(OH)2+ ]= Ka KSh2 / Ke3 (4)

Al(OH)3(solide) + OH– = Al(OH)4– ; K= [Al(OH)4–] / [OH–] = [Al(OH)4–] h / Ke d'où : [Al(OH)4–]= K Ke /h (3)

s = KSh3 / Ke3 + Ka KSh2 / Ke3 + K Ke /h.

x1 = [Al3+]/s = KSh3 / Ke3 / [KSh3 / Ke3 + Ka KSh2 / Ke3 + K Ke /h]

x1 =1 / [1+ Ka/h +KKe4/(Ksh4)]= 1/[1+10-5/h+10-21/h4]

x2 = [Al(OH)2+]/s=Ka KSh2 / Ke3 / [KSh3 / Ke3 + Ka KSh2 / Ke3 + K Ke /h]

x2 = 1/[ h/Ka+1 + KKe4 /(Ka KSh3 )] =1/[105h+1+ 10-16/h3]

x3 = [Al(OH)4–]/s = K Ke /h / [KSh3 / Ke3 + Ka KSh2 / Ke3 + K Ke /h]

x3 =1/[KKe4KSh4 ) +Ka KSh3 /(KKe4) +1] = 1/[10-85h4+1016/h3 + 1]

A graphe correspondant à x1 car Al3+ est prépondérant en milieu acide.

B graphe correspondant à x3 car Al(OH)4– est prépondérant en milieu basique.

C : graphe correspondant à x2.

Le précipité Al(OH)3(solide) apparaît dès que c0>s.

En milieu acide Al3+ est prépondérant et s voisin de [Al3+] = KSh3 / Ke3.

KSh3 / Ke3 <c0 ; log Ks + 3 log h - 3 log Ke < log c0 ; pKs+3pH-3pKe>-log c0 ;

3pH >3pKe -log c0 - pKs ; pH > pKe -(log c0 + pKs) /3

à la limite : pH1 = 14 -( log 0,5 +32)/3 = 3,4. ( h= 4 10-4 mol/L)

L'approximation faîte est-elle justifiée ?

x1 = 1/[1+10-5/h+10-21/h4] voisin de 1/1,025 = 1

x2 = 1/[105h + 1 + 10-16/h3] voisin de 1 / 41 = 0,024 négligeable devant x1.

x3 = 1/[10-85h4+1016/h3 + 1] voisin de 1/(6,4 105) = 0

L'approximation est donc acceptable.

A pH fortement basique, Al(OH)4– est prépondérant. c0 = [Al(OH)4–] = K Ke /h

h = K Ke /c0 ; log h = log K + log Ke - log c0 ; pH2 = pK+pKe+log c0 = -3+14 + log 0,5 = 10,7.(h= 2 10-11)

L'approximation faîte est-elle justifiée ?

x1 = 1/[1+10-5/h+10-21/h4] voisin de 0

x2 = 1/[105h + 1 + 10-16/h3] voisin de 0

L'approximation est donc justifiée

Lasolubilité s est minimum si la dérivée ds/dh=0.

s = KSh3 / Ke3 + Ka KSh2 / Ke3 + K Ke /h.

ds/dh = 3 KSh2 / Ke3 + 2Ka KSh / Ke3 -K Ke/h2 = 0

3 KSh4 / Ke3 + 2Ka KSh3 / Ke3 -K Ke=0

3 1010h4 + 2 105h3-10-11 = 0

solution : pH voisin 5,4.( h = 4 10-6 mol/L)

Calculons la solubilité s pour cette valeur de pH :

s = KSh3 / Ke3 + Ka KSh2 / Ke3 + K Ke /h

s = 1010 h3 + 105 h2 + 10-11/h = 6,3 10-7 + 1,6 10-6 + 2,5 10-6 = 4,7 10-6 mol/L

si c0 est inférieure à 4,7 10-6 mol/L, le précipité ne se forme pas.
retour -menu