Aurélie 05/06
Le carbone 14 : d'après concours manipulateur électroradiologie médicale Toulouse 2006

Google

Transformations nucléaires. (12 pts)

Données : M(C)=12,0 g/mol ; NA= 6,02 1023 mol-1 ; ln 2 = 0,69 ; ln 1,64 10-2 = -4,1.

Dans la nature l'élément carbone possède deux noyaux isotopes: le carbone 12 noté 126C et le carbone 14 noté 146C. Le carbone 14 se forme dans la haute atmosphère à la suite d'un choc entre un neutron et un noyau d'azote 14 : 147N. Ce carbone 14 est radioactif b- et a un temps de demi-vie égal à 5570 ans.

On note l la constante radioactive du carbone 14. On note N(t) le nombre de noyaux radioactifs présents à l'instant t dans l'échantillon. L'activité d'un échantillon radioactif A(t) est le nombre de désintégrations qu'il produit par unité de temps soit A(t) = -dN(t) / dt.

Dans la matière vivante, les échanges d'élément carbone entre l'organisme végétal ou animal et l'air atmosphérique font que le rapport N(carbone14) / N(carbone 12) est constant. A la mort de l'être vivant, ces échanges prennent fin ce qui entraîne la décroissance de ce rapport. Dans 200 g d'os d'un être vivant, il y a 1,0 g de carbone et on mesure 15 désintégrations par minute.

  1. Après avoir énoncé les lois utilisées, écrire l'équation de la réaction nucléaire correspondant à la formation du carbone 14 dans l'atmosphère. Quelle est la seconde particule formée ?
  2. Définir la radioactivité.
    - Ecrire l'équation de la désintégration     b- du carbone 14.
  3. Exprimer A(t) en fonction de N(t) et l.
    - En déduire l'équation différentielle vérifiée par le nombre N(t) de noyaux.
  4. Vérifier que l'expression N(t) = N0 exp(-lt) est solution de cette équation.
  5. Définir le temps de demi-vie.
    - A un instant pris comme origine des temps, l'activité d'un échantillon est notée A0. Exprimer en fonction de A0, l'activité de cet échantillon aux instants t½, 2 ½, 3½, 4½, et 5½.
  6. Tracer l'allure de la courbe représentant l'évolution de l'activité de l'échantillon en fonction du temps. Déduire des questions 3 et 4 l'équation de la courbe obtenue.
  7. Etablir la relation entre l et t½. Calculer l pour le carbone 14 et préciser son unité.
  8. Dans 200 g d'os trouvés sur un site archéologique, l'analyse montre que le rapport N/N0=1,64 10-2. Clalculer l'âge T de ces ossements en justifiant.
  9. Quelle est en Bq l'activité de ces ossements ?
    - Quel est le nombre N0 de noyaux radioactifs présents dans l'échantillon ?
  10. En supposant qu'il n'y ait que des noyaux de carbone 12 dans l'échantillon, quel est le nombre total de noyaux de carbone dans 200 g d'os ? Comparer ce nombre à N0 et commenter ce résultat.

corrigé
équation de la réaction nucléaire correspondant à la formation du carbone 14 dans l'atmosphère :

147N + 10n = AZX +146C

conservation du nombre de nucléons : 14 +1= A+14 soit A= 1.

conservation de la charge : 7=Z+6 soit Z= 1 , donc X est un noyau hydrogène11H ou proton

radioactivité :

Un noyau radioactif est un noyau instable dont la désintégration (destruction) aléatoire s'accompagne:

  • L'apparition d'un nouveau noyau
  • L'émission d'une particule notée a, b - ou b +
  • L'émission d'un rayonnement électromagnétique noté g.
La radioactivité est une réaction dite nucléaire car elle concerne le noyau de l'atome alors que les réactions chimiques ne concernent que le cortège électronique sans modifier le noyau.

équation de la désintégration b- du carbone 14 :

146C = AZX + 0-1e

conservation de la charge : 6=Z-1 soit Z= 7 , donc X est l'élément azote N

conservation du nombre de nucléons : 14 = A+0 soit A= 14.

A(t) en fonction de N(t) et l : A(t) = l N(t)

équation différentielle vérifiée par le nombre N(t) de noyaux :

A(t) = -dN(t)/dt et A(t) = l N(t)

d'où : dN(t)/dt + l N(t) =0 (1)

N(t) = N0 exp(-lt) ; dériver par rapport au temps : dN(t)/dt = -lN0 exp(-lt) = -lN(t)

repport dans (1) : -lN(t) + l N(t) =0 est vérifié pout tout t

donc N(t) = N0 exp(-lt) est solution de (1).

temps de demi-vie :

La demi-vie radioactive,(ou période) notée t½, d'un échantillon de noyaux radioactifs est égale à la durée au bout de laquelle la moitié des noyaux radioactifs initiaux se sont désintègrés.

activité de cet échantillon aux instants t½, 2 ½, 3½, 4½, et 5½ :

A(t½) = A0/2 ; A(2t½) = A0/22 ; A(3t½) = A0/23 ; A(4t½) = A0/24 ; A(5t½) = A0/25 .

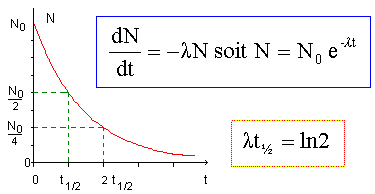
de même A(t) =A0 exp (-lt)

relation entre l et t½ :

à t = t½, A(t½) = ½A0 = A0 exp (-lt½) ; 0,5 = exp (-lt½) ; ln 0,5 = -lt½ ; ln2 = lt½

dans le cas du carbone 14 : l= ln2/t½ = 0,69 / 5570 =1,24 10-4 an-1.

ou bien 0,69/(5570*365*24*3600) = 3,93 10-12 s-1.

l'âge T de ces ossements :

N/N0=1,64 10-2 ; d'autre part N/N0=exp(-lT)

ln 1,64 10-2 = -4,1 = -lT ; T= 4,1 / l= 4,1 / 1,24 10-4 =3,30 104 ans.

activité de ces ossements :

Dans 200 g d'os d'un être vivant, il y a 1,0 g de carbone et on mesure 15 désintégrations par minute ; A0 = 15/60 = 0,25 Bq.

A(t)/A0=1,64 10-2 ; A(t) = 1,64 10-2A0= 1,64 10-2 *0,25 = 4,1 10-3 Bq.

nombre N0 de noyaux radioactifs présents dans l'échantillon :
A0 = l N0 ; N0 = A0 / l = 4,1 10-3/ 3,93 10-12=1,0 109 noyaux de carbone 14.

En supposant qu'il n'y ait que des noyaux de carbone 12 dans l'échantillon, nombre total de noyaux de carbone dans 200 g d'os :

masse de carbone (g) / masse molaire (g/mol) = 1/ 12 mol de carbone 12

puis 1/12 NA =6,02 1023/12 = 5,0 1022 noyaux de carbone12, valeur très supériuere à N0.
retour -menu