Aurélie 21/12/05
Dipole LC+ diode, oscillateur élastique horizontal, lentille + miroir, utiliser un oscilloscope

d'après concours technicien laboratoire 97 ( physique )

Google

Dipole LC + diode

C= 10 mF, u0=30 V ; L= 10 mH ( bobine et diode sont parfaites). Le condensateur est initialement chargé sous la tension de 30 V.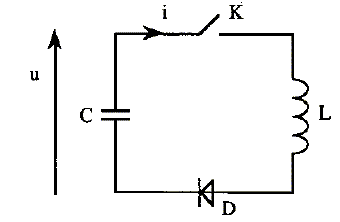

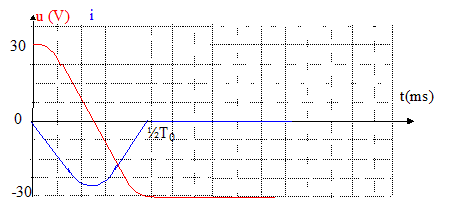
  1. A t=0 on ferme l'interrupteur K. Exprimer les dérivées di/dt et du/dt en fonction de u, i, L et C. Caractériser les grandeurs u et i lorsqu'intervient la diode.
  2. Dessiner l'allure de la tension u(t) et i(t) pout t>0.
  3. Quelle est la bonne expression de la pulsation propre w0 en montrant qu'elle équivaut à une égalité entre deux impédances que l'on précisera.
  4. Préciser l'échelle des temps sur le graphe précédent.
     
corrigé
A la fermeture de l'interrupteur le condensateur se décharge à travers la bobine, la diode étant passante : la bobine stocke de l'énergie.

u(t) = u0 cos (w0t) avec w²0 = 1/(LC) ; du/dt = - w0u0 sin (w0t)

La charge des armatures du condensateur diminue : q= Cu soit dq/dt = - w0Cu0 sin (w0t)

Or l'intensité du courant est : i = -dq/dt lors de la décharge : di/dt = -d²q/dt² = w²0 Cu0 cos (w0t) = w²0 C u.

à t > T0/4, la bobine libère l'énergie qu'elle a mis en stock et le condensateur se charge en sens inverse de la charge précédente : la diode est passante.

à t>½T0, le condensateur ne peut plus se décharger car la diode devient non passante. ( le condensateur étant chargé en sens contraire, le courant de décharge aurait le sens contraire du courant précédent).

expression de la pulsation propre w0 = 1 / racine carrée (LC)

L'impédance de la diode passante est nulle ; la valeur de l'impédance de la bobine Lw0 est égale à la valeur de l'impédance du condensateur ( 1 / (Cw0)

Par suite on retrouve LCw²0 = 1 ou bien w0 = 1 / racine carrée (LC)

L= 10-2 H ; C= 10-5 F ; LC= 10-7 ; (LC)½ = 3,16 10-4 ; w0 =3162 rad/s ; T0 = 2p / w0 = 2 ms.

Oscillateur élastique horizontal

k : raideur du ressort ; frottement négligés.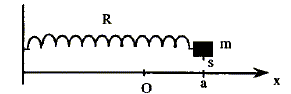

Lorsque le ressort est au repos, l'index fixé sur la masse m est en O, d'abscisse x=0. On tend le ressort afin d'amener l'index en s d'abscisse x=a positif. On libère la masse m à la date t=0.

  1. Représenter graphiquement l'allure des variations de l'abscisse x(t) de l'index s et de sa vitesse v(t).
  2. Montrer que la période propre de cet oscillateur est T0 = 2p racine carrée (m/k).
  3. Si k= 20 N/m, calculer la valeur de la masse m pour que la durée du mouvement de la masse vers la gauche soit 0,25 s.
corrigé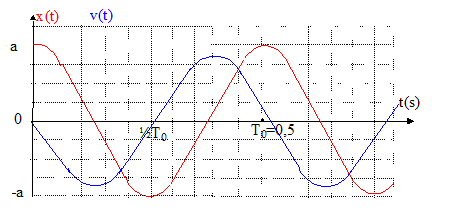

abscisse de l'index : x(t) = a cos (w0t) avec w0 = k/m

la vitesse est la dérivée de l'abscisse par rapport au temps : v(t) = x'(t) = - a w0 sin (w0t).

La période propre de cet oscillateur est :

énergie initiale du système {masse + ressort}est sous forme potentielle élastique : ½ka²

Au passage à la position d'équilibre l'énergie est sous forme cinétique : ½m v² = ½m x'²

énergie du système à une date quelconque : ½kx² + ½mv²

Pas de frottements: l'énergie mécanique est constante : ½ka² =½kx² + ½mv²

Dériver par rapport au temps : 0= kx x' + mv v' avec x' = v et v' = x"

d'où : kx + m x" = 0 ; on pose w²0 = k/m

période : T0 = 2p/w0= 2p racine carrée (m/k).

valeur de la masse m pour que la durée du mouvement de la masse vers la gauche soit 0,25 s :

On en déduit la période : 2*0,25 = 0,5 s.

m=T²0 k / (2p)² =0,5² * 20 / 6,28² =0,127 kg.

Lentille mince + miroir plan

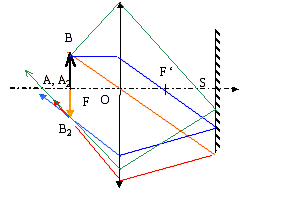
On dispose d'une lentille mince L, d'un miroir plan M et d'un petit objet lumineux AB situé dans le plan d'un écran E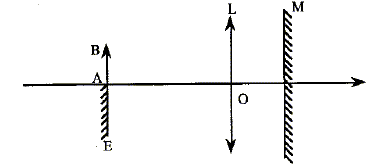

  1. Indiquer comment on peut tirer parti de ce matériel pour mesurer la distance focale f' de L de manière simple. On précisera quelle doit être la position de L et ce que l'on doit observer et mesurer.
  2. Tracer la marche d'un rayon lumineux issu de B et s'appuyant sur le bord supérieur de la lentille lorsque le système est réglé pour la mesure.
corrigé
Déplacer le miroir et la lentille de telle manière que l'image A'B' de l'objet AB se forme sur l'écran E. Cette image renversée doit avoir la même hauteur que l'objet AB.

La distance lentille écran est égale à la distance focale. La distance lentille miroir est égale à deux fois la distance focale. 
Utiliser un oscilloscope

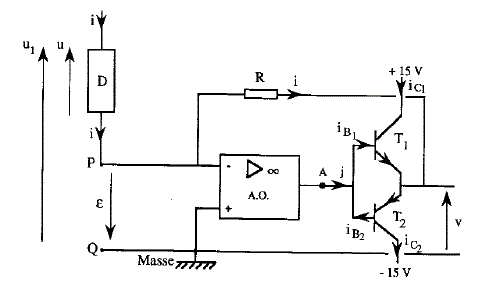
On désire visualiser ensemble les oscillogrammes de la tension u(t) appliquée à un dipôle D et de l'intensité i(t) du courant qui le parcourt.

On dispose d'un générateur de tension G dont les bornes de sorties sont isolées de la masse, de résistance r de faible valeur ( 1,0 W ) et d'un oscilloscope classique à deux voies. La masse M et les entrées A et B de l'oscilloscope sont représentées sur la figure.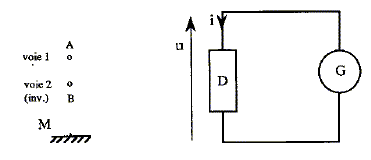

  1. Proposer une solution et représenter les cablages. Faut-il ou non inverser la voie 2 ?
  2.   On réalise l'observation précédente en utilisant le montage ci-dessous. Il s'agit d'un capteur de courant qu'il faut insérer dans le circuit dont fait partie le dipôle D ; les bornes d'entrée de ce capteur sont P et Q.

    L'amplificateur opérationnel est considéré comme parfait.

    - On applique la tension u1 sur la voie 1 de l'oscilloscope. Pourquoi est-elle égale à la tension u ? La tension v est appliquée sur la voie 2 ( inversée) de l'oscilloscope. Exprimer v en fonction de i.
    - Avec R= 10 W calculer v si i= 250 mA. Quel est le transistor qui conduit ? ( T1 ou T2) Est-il saturé ou fonctionne-t-il linéairement ?
    - Sachant que le coefficient d'amplification du courant de ce transistor ( b) est égal à 100, calculer j, intensité du courant de sortie de l'A.O.
    Quel est le rôle de la paire de transistors complémentaires T1 et T2 ?

 

corrigé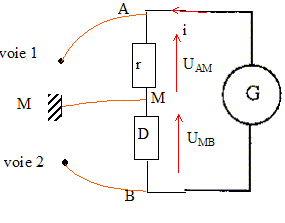

voie 1 : on visualise UAM, tension aux bornes d'un résistor, image de l'intensité au facteur r près.

voie 2 : on visualise UBM, opposée de la tension aux bornes du dipôle D : il faut inverser la voie 2.

u1 = u -e avec e =0 ( A.O parfait)

e + Ri + v = 0 soit v = - Ri

La voie 2 de l'oscilloscope est inversée, on visualise donc -v = Ri = 10*0,25 = 2,5 V.

Transistor T1 passant, régime linéaire.

Ces deux transistors ainsi montés se comportent comme un transistor unique, dont le gain ß est égal au produit des gains des deux transistors. Grâce à ce montage, on obtient une forte amplification en intensité.

j= i/ b² = 0,25 / 104 = 2,5 10-5 A
retour -menu