Aurélie 04/06
Etude de la réponse d'un enregistreur graphique à une tension d'entrée sinusoïdale : concours technicien laboratoire 2006

Google

Etude de la réponse d'un enregistreur graphique à une tension d'entrée sinusoïdale

L'enregistreur graphique positionne son traceur dans le plan (Ox, Oy) d'une feuille de papier à unabscisse variable x(t) proportionnelle à une tension issue de sa base de temps interne et une ordonnée variable y(t). Cette ordonnée est proportionnelle à une tension électrique s(t), elle même commandée par la tension e(t) que l'on veut enregistrer sur une feuille de papier. y(t) et s(t) sontliées par la relation y(t) = K s(t) avec K= 10-2 m V-1.

On considèrera dans toute l'étude le système noté H commandé par la tension d'entrée e(t) délivrant la tension de sortie s(t), représenté figure 1 :

On applique à l'enregistreur graphique une tension sinusoïdale e(t) d'amplitude EM, de fréquence f, d'équation e(t) = EM sin (2p f t+j). Le traceur inscrit sur la feuille de papier une courbe sinusoïdale d'équation y(t) = YMsin (2p f t+jY). Les formes d'onde de cette tension e(t) et de la réponse de l'ordonnée y(t) du traceur sont données figure 2.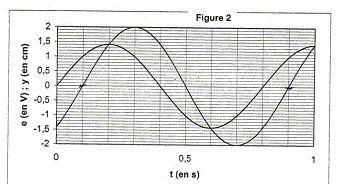

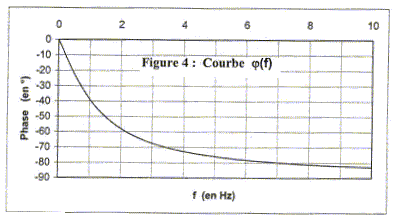
  1. Que valent à la date t=0 s, e(t) et y(t).
  2. Indiquer comment identifier sur la figure 2 les courbes représentatives des fonctions e(t) et y(t).
  3. Rappeler la relation entre la fréquence f et la période T, puis celle entre la fréquence f et la pulsation w d'une grandeur sinusoïdale. Déterminer graphiquement T, en déduire f et w.
  4. Rappeler la relation entre la valeur efficace E et l'amplitude EM d'une grandeur sinusoïdale. Calculer E et EM.
  5. Déterminer graphiquement l'amplitude YM de y(t) et le déphasage jY de y(t) par rapport à e(t).
  6. Déterminer l'amplitude SM de s(t) et le déphasage j de s(t) par rapport à e(t). En déduire la valeur du rapport S/E.
    Dans la suite on note E et S les grandeurs complexes associées respectivement aux tensions e(t) et s(t). Le système H est assimilé à un système linéaire du premier ordre et présente une transmittance complexe H= H0/(1+jwt) avec H0=2 et t =0,127 s.
  7. Exprimer le module |H| de H en fonction de H0, w, t et calculer sa valeur numérique pour f= 1,25 Hz et le comparer à S/E.
  8. Exprimer l'argument j et calculer sa valeur numérique pour f=1,25 Hz
  9. On rappelle que le gain GdB= 20 log |H|. Que valent |H|, GdB et j pour les valeurs suivantes de la fréquence : 0 ; 1 ; 2 ; 4 ; 8 ; 10. On présentera les résultats dans un tableau.
  10. A quel type de filtre ce système est-il analogue ? Quel est son ordre ? pourquoi ?
  11. Que vaut la fréquence de coupure fc à -3 dB du gain maximum ? L'ordre de grandeur de cette fréquence est-il acceptable dans le cas de ce système électromécanique ? Justifier.
  12. Exprimer E en fonction de H0, w, t et S. En déduire en identifiant d/dt à jw, l'équation différentielle liant e(t) et s(t) en régime variable quelconque.

corrigé
identifier les courbes représentatives des fonctions e(t) et y(t).

e(t) est la fonction de commande, en avance sur y(t) la fonction commandée

d'après la figure 2 : e(0) = 0 V ; y(0)= -1,5 cm

période T (s) = 1/ fréquence (Hz) ; w = 2pf.

T= 0,8 s ; f = 1/0,8 = 1,25 Hz ; w = 6,28*1,25 = 7,85 rad/s.

relation entre la valeur efficace E et l'amplitude EM d'une grandeur sinusoïdale : EM= racine carrée (2) E = 2½E
EM=1,4 V (lecture graphe) d'où E= 1,4 / 2½ = 1 V

amplitude YM de y(t) et le déphasage jY de y(t) par rapport à e(t): YM= 2 cm = 0,02 m

jY = - 0,1 s soit -T/8 soit -2p/8 = - 0,78 rad.

amplitude SM de s(t) et le déphasage j de s(t) par rapport à e(t) :

y(t) = 0,01 y(t) soit s(t) = 100 y(t) d'où SM = 100YM=100*0,02 = 2 m ; S=SM / 2½= 1,42 V ; j =jY.

rapport S/E = 1,42 / 1 = 1,42.

module de H en fonction de H0, w, t :

H= H0(1-jwt) / (1+(wt)2) = H0(1+(wt)2)-½ = 2 (1+(7,85*0,127)²)-½ =0,708 *2 = 1,42, valeur égale à S/E.

argument j : tan j = -wt = -7,85*0,127 = -0,996 soit j =-0,78 rad, valeur égale à jY.
f(Hz)
0
1
2
4
8
10
|H|
2
1,5
1,05
0,6
0,3
0,25
GdB
6
3,5
0,4
-4,4
-10
-12
j
0
-40
-60
-72
-81
-83
type de filtre : passe bas d'ordre 1 ( d'après l'expression de la fonction de transfert, le dénominateur de H est un polynôme du 1er degré )

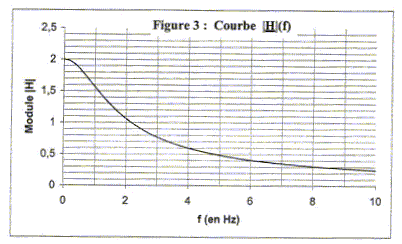
fréquence de coupure fc à -3 dB du gain maximum :

-3 = 20 log |H| d'où log |H| = -3/20 = -0,15 ; |H| =10-0,15 = 0,707

lecture figure 3 : fc = 3,4 Hz.

L'ordre de grandeur, très faible, de cette fréquence est acceptable dans le cas de ce système électromécanique.

Exprimer E en fonction de H0, w, t et S : E = S (1+jwt) /H0.

équation différentielle liant e(t) et s(t) en régime variable quelconque :

e(t) = 1/H0 [ (s(t) + td(s(t)/dt]

retour -menu