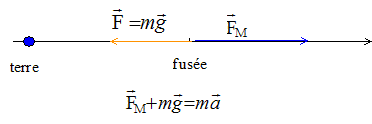1 u = 1,6605 10^-27 kg ; 1 eV= 1,602 10^-19 J; N_A= 6,022 10²³ mol^-1; c= 2,998 10⁸ m/s ; masse d'un neutron m_n= 1,00866 u ; pouvoir calorifique du pétrole P_cp=42,00 MJ kg^-1.

nom et symbole de l'élément	uranium 235 U	zirconium 95 Zr	tellure 138 Te
n° atomique	92	40	à déterminer
masse en u	234,993	94,8860	137,901

Thorium Th (Z= 90) ; protactinium Pa ( Z=81) ; neptunium Np ( Z= 93) ; plutonium Pu ( Z=94)

Dans une centrale nucléaire à neutrons lents, le combustible est l'uranium 235 enrichi. Il contient 3% d'uranium 235 fissile et 97% d'uranium 238 non fissile. Lors de la fission d'un noyau d'uranium 235 sous l'impact d'un neutron, plusieurs réactions sont possibles. La plus fréquente donne des noyaux de zirconiim 95 et de tellure 138 ainsi qu'un ou plusieurs neutrons.

1. Ecrire la réaction de fission. Justifier.
2. Calculer en MeV l'énergie E₁ libérée par cette réaction nucléaire.
3. Calculer en J l'ordre de grandeur de l'énergie E₂ libérée par la fission de 1,000 g d'uranium 235.
4. Calculer la masse de pétrole libérant par combustion la même énergie. Conclure.
5. L'uranium 238 non fissile du réacteur se transforme par capture d'un neutron lent en un noyau radioactif. Ce dernier subit deux désintégrations b^- pour se transformer en un noyau fissile. Ecrire les équations des deux réactions nucléaires afin d'identifier le noyau fissile formé.

Une fusée de masse m se dirige vers la Lune. Ses occupants ont pour mission d'y déposer à sa surface des réflecteurs à rayon laser afin de pouvoir mesurer précisément la distance Terre- Lune.

I- En route vers la Lune : depuis la Terre des scientifiques suivent le déplacement de la fusée.

Position A : elle est située à h_A= 8,0 10³ km de la surface de la Terre et avance à la vitesse v_A= 11 km/s

Position B : elle est située à h_B= 1,0 10⁴ km de la surface de la Terre et avance à la vitesse v_B= 13 km/s

1. Exprimer en fonction des données, la valeur g du champ de gravitation crée par la Terre, à une altitude h, dans la position A puis dans la position B. Faire les application numérique.
   Dans la suite de l'exercice, on supposera que ce champ de gravitation varie peu entre les positions A et B ; il sera pris égal à la moyenne des deux valeurs trouvées. On négligera l'attraction gravitationnelle de la Lune.
2. La fusée est suposée se dirigée sur une droite reliant le centre de la Terre et le centre de la Lune. La force motrice du moteur de la fusée est modélisée par une force constante de valeur F_M.
   - Représenter sur un schéma les forces s'exerçant sur la fusée entre les positions A et B
   - Déterminer l'expression littérale de la valeur F_M de la force motrice.
   - Déterminer l'expression littérale de la valeur a de l'accélération de la fusée entre les deux positions A et B. Faire l'application numérique.
   - Comparer l'accélération d'un membre de l'équipage à celle de la fusée. L'équipage flotte-t-il dans la cabine ? Justifier.

II- Sur la Lune : ils déposent plusieurs réflecteurs sur la Lune. Depuis la Terre les scientifiques visent l'un des réflecteurs à l'aide d'un faisceau laser et mesure la durée Dt= 2,51 s séparant l'émission de la réception. Déterminer la distance séparant les centres des deux astres.

On souhaite déterminer expérimentalement l'inductance d'une bobine par deux méthodes différentes.

A- méthode 1 : on réalise le montage suivant comprenant un générateur basses fréquences délivrant une tension périodique triangulaire, une bobine d'inductance L inconnue et de résistance interne r et un conducteur ohmique de résistance R=1,00 kW. Dans cette méthode on négligera r devant R.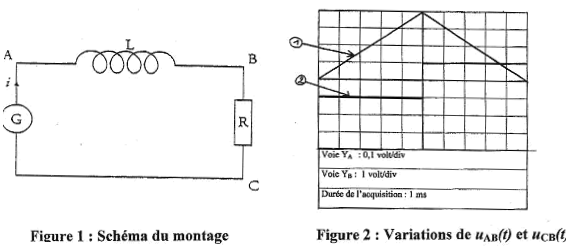

Un oscilloscope numérique permet de visualiser la tension u_AB(t) aux bornes de la bobine et de la tension u_CB(t) aux bornes de la résistance R. Le GBF ayant une masse flottante, cela permet de relier la masse de l'oscilloscope à n'importe quel point du circuit.

1. Recopier le schéma de la figure 1 et indiquer les branchements de l'oscilloscope sachant que la voie Y_A correspond à la tension u_AB(t) et Y_B à la tension u_CB(t).
2. Identifier les signaux 1 et 2 enregistrer sur les voies Y_A et Y_B en justifiant.
3. Exprimer l'inductance L de la bobine en fonction des tensions u_AB(t) et u_CB(t).
4. Calculer la valeur de l'inductance L.
5. Calculer l'énergie emmagasinée dans la bobine à l'instant t= 0,6 ms.

B- méthode 2 : un condensateur de capacité C= 2 mF est chargé à l'aide d'un générateur de tension, il est ensuite déconnecté du générateur. A la date t=0, le condensateur chargé est relié à la bobine de la partie précédente. Les variations au cours du temps de la tension u_C(t) aux bornes du condensateur sont enregistrées à l'aide d'un système d'aquisition de données relié à un ordinateur.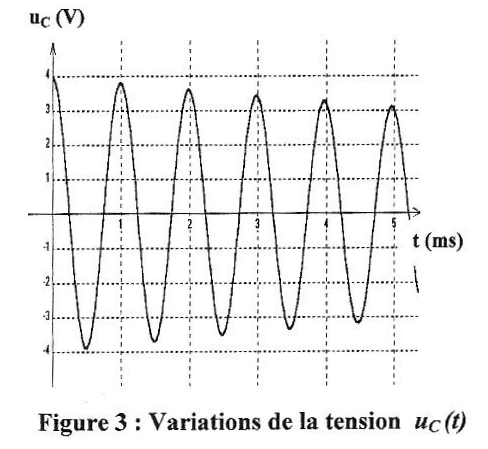

1. Ecrire l'équation différentielle à laquelle satisfait la tension u_C(t).
2. Calculer la valeur de l'inductance de la bobine en considérant que la mesure de la pseudo-période est identique à celle de la période propre.

---

corrigé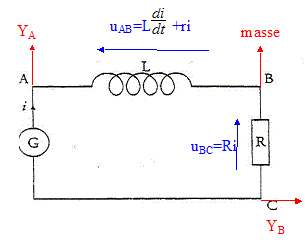

---

sur la voie Y_B on visualise u_CB(t) = -Ri, tension triangulaire (1) ( ou affine par intervalle)

sur la voie Y_A on visualise u_AB(t) = Ldi/dt ( si le terme r i est négligeable) , tension constante (2) par intervalle car la dérivée di/dt d'une fonction affine est constante

Expression de l'inductance L de la bobine en fonction des tensions u_AB(t) et u_CB(t).

sur l'intervalle de temps [0 ; 0,5 ms] : u_CB(t)= -Ri ; du_CB(t)/dt =-R di/dt = 4 / 5 10^-4 = 8000 V s^-1 d'où di/dt = -8000/1000 = -8 A s^-1.

u_AB(t) = Ldi/dt = -L/R du_CB(t)/dt soit L= - R u_AB(t) / (du_CB(t)/dt) avec u_AB(t) = -0,1 V

L= 100/ 8000 = 0,0125 H.

énergie emmagasinée dans la bobine à l'instant t= 0,6 ms : u_CB(0,6)= 3 V ; u_CB(t)= -Ri soit i = -3 /R = - 3 10^-3 A.

énergie stockée : E= ½Li² =0,5*0,0125*9 10^-6 = 5,6 10^-8 J.

équation différentielle à laquelle satisfait la tension u_C(t)

u_C(t) + Ldi/dt +ri =0

d'autre part q= Cu_C(t) et i = dq/dt = Cdu_C(t)/dt ; di/dt = Cd²u_C(t)/dt²

u_C(t) + LCd²u_C(t)/dt² + rCdu_C(t)/dt =0

valeur de l'inductance de la bobine : période T= 10^-3 s ( lecture graphe)

d'autre part T= 2p(LC)^½ ; LC= T²/(4p²) ; L= T²/(4p²C) = 10^-6 / (4*3,14² *2 10^-6 )=1,27 10^-2 H.