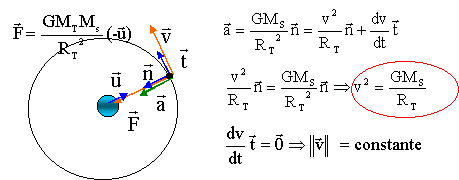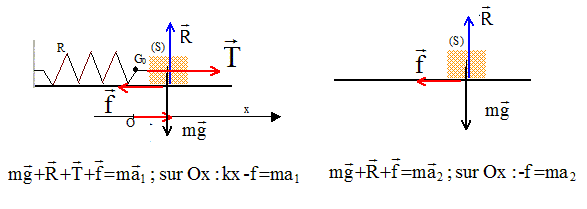Aurélie 05/06
d'après concours manipulateur électroradiologie médicale Rennes 2006

Google

3ème loi de Kepler

I- On étudie le mouvement d'un satellite de Saturne de masse MT (ou m) en révolution autour de la planète Saturne de masse MS ou M. La trajectoire de ce satellite est circulaire de rayon RT ou r.

  1. Donner la formule vectorielle de l'interaction gravitationnelle s'exerçant sur ces deux astres.
  2. Quelle est l'hypothèse à formuler sur ces deux astres pour pouvoir utiliser la formule de la question précédente ?
  3. En supposant le référentiel Saturnocentrique comme galiléen, établir l'expression de la vitesse v du satellite en fonction de G, M et r. Quel est le mouvement du satellite ?
  4. Définir la période T de révolution, et montrer que cette dernière est proportionnelle à r1,5.(3ème loi de Kepler)

II- La masse de Saturne : la planète Saturne a de nombreux satellites qui ont des trajectoires quasi-circulaire autour de la planète.
satellite
Janus
Minas
Encelade
Thethys
Diione
Titan
période T (jour)
0,75
0,94
1,37
1,9
2,7

rayon r ( 104 km)
16,0
18,6
24,0
29,4
37,8
121,2

  1. Montrer que ces satellites suivent la 3ème loi de Kepler.
  2. En déduire la masse de Saturne
  3. Calculer la période de révolution de Titan. G= 6,67 10-11 SI.
corrigé
hypothèse à formuler sur ces deux astres : astres à répartition de masse à symétrie sphérique.

 

expression de la vitesse v du satellite v = (GM/r)½.

Dans le référentiel saturno-centrique écrire la seconde loi de Newton, appliquée à Titan, ( assimilé à son centre d'inertie T).

l'accélération vectorielle et la force gravitationnelle sont colinéaires et de même sens : l'accélération est donc centripète et sa composante tangentielle est nulle.

alors dv/dt =0 entraîne v= constante. Le mouvement est uniforme ( de plus il est circulaire) .

période T de révolution : durée pour décrire une circonférence de longueur 2pr à vitesse constante v. T= 2pr / v.

v= (GM/r)½ ou v² = GM/r

élever l'expression de la période au carré : T²= 4p2r2/v2 ;

remplacer v² par son expression : T²= 4p2r3/(GM)

soit T² / r3 = 4p2 / (GM) 3ème loi de Kepler. ou en core T= 2p/(GM)½ r1,5.

T(s)
6,48 104
8,12 104
1,18 105
1,64 105
2,3 105
T² ( s²)
4,2 109
6,6 109
1,4 1010
2,7 1010
5,4 1010
r (m)
1,6 108
1,86 108
2,4 108
2,94 108
3,78 108
r3 ( m3)
4,1 1024
6,43 1024
1,38 1025
2,5 1025
5,4 1025
T² / r3
1,03 10-15
1,03 10-15
1,01 10-15
1,06 10-15
1,0 10-15
à 6 % près, T² / r3 est constant : la 3ème loi de Kepler est vérifiée.

masse de Saturne : 4p2 / (GM) = 1,03 10-15 ; M= 4p2 / (G 1,03 10-15) = 4*3,14²/(6,67 10-11*1,03 10-15)= 5,7 1026 kg.

période de révolution de Titan : T²= 1,03 10-15 r3 =1,03 10-15 * (1,212 109)3 = 1,83 1012.

T= 1,35 106 s = 15,7 j.

Mécanique

I- Déplacement d'une masse sur une surface rugueuse :

Un bloc de masse m est maintenu au point A contre un ressort comprimé, de constante de raideur k, sans lui être attaché. Le ressort est comprimé de DL. A t=0, le bloc glisse sur une surface horizontale rugueuse. Il parcourt une distance d, avant de s'immobiliser au point B.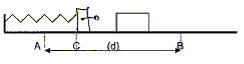

  1. Expliquer qualitativement les différentes phases du mouvement de ce bloc de masse m depuis le moment du lâcher jusqu'à l'arrêt. Justifier.
  2. Faire le schéma des forces exercées sur le bloc lorsque le bloc est au contact du ressort, lorsque le bloc n'est plus en contact du ressort.
  3. Donner l'expression de l'énergie mécanique en A et en B.
  4. La variation de cette énergie mécanique est égale au travail des forces de frottement f. Calculer la valeur de f supposée constante.
  5. Calculer la vitesse du bloc en C, au moment où il quitte le ressort.

DL= 20 cm ; k = 50 N/m ; m=0,2 kg ; longueur à vide du ressort L0 = 40 cm ; d = 0,5 m.

II- Cette fois on attache le bloc au ressort. On déplace le bloc au point A, en comprimant le ressort. A t=0 on lâche le système {masse + ressort }. La surface horizontale sur laquelle glisse le bloc est identique à celle de la question préédente.

  1. Faire l'inventaire des forces appliquées au système à une date t.
  2. Etablir l'équation différentielle du mouvement.
  3. Quelle est la nature du mouvement de cet oscillateur ?
corrigé
les différentes phases du mouvement : mouvement rectiligne

bloc contre le ressort : accéléré ( accélération non constante) ;

bloc séparé du ressort : uniformément freiné puis arrêt.

expression de l'énergie mécanique en A et en B :

en A l'énergie mécanique est sous forme potentielle élastique EA= ½kDL².

en B l'énergie mécanique est nulle EB=0

valeur de f supposée constante : EB-EA= - ½kDL² = Wf A-->B = -f AB = -fd

f = kDL² / (2d) = 50*0,2²/(2*0,5) = 2 N.

vitesse du bloc en C : énergie mécanique en C : EC= ½mv²

travail des frottements entre A et C : Wf A-->C = -f AC = -f (L0-DL)

diminution de l'énergie mécanique entre A et C = travail des frottements : ½mv²- ½kDL² = -f (L0-DL)

½mv² = ½kDL²-f (L0-DL) = 25*0,2² -2(0,4-0,2) = 1-0,4 = 0,6 J ; v² = 1,2/0,2 =6 ; v = 2,4 m/s.

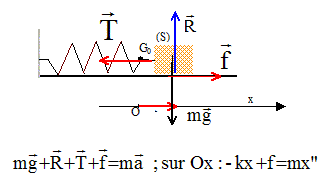
inventaire des forces appliquées au système à une date t :

écrire la seconde loi de Newton sur l'axe Ox ( O position d'équilibre, ressort non déformé ):

équation différentielle du mouvement : -kx+f = mx" soit mx"+kx = f

nature du mouvement : rectiligne, périodique, amorti.
Chimie

Electrolyse :

On envisage de chromer ( Cr) entièrement un pare-chocs métallique en y déposant une couche de chrome, d'une épaiseur e=50 mm. Le parre-chocs est considéré comme un bloc parallèlépipédique de longueur L= 2,0 m, de largeur l=0,10 m, de hauteur h= 5,0 mm. On plonge le parre-chocs dans une solution contenant des ions chrome III Cr3+, puis on électrolyse cette solution, entre l'électrode constituée par le parre-chocs et une seconde électrode de nature adéquate. L'opération dure 10 heures et son rendement est 95%.

  1. Ecrire l'équation de la réaction d'électrode qui permet la formation du chrome métallique à partir des ions chrome III.
    - Le parre-chocs constitue-t-il l'anode ou la cathode de l'électrolyseur . Est-ce le pôle positif ou négatif de l'électrolyseur ?
  2. Calculer le volume de la couche de chrome à déposer.
    - En déduire la masse m(Cr) de chrome, puis la quantité de matière n(Cr) en mol.
    - Indiquer la relation liant n(Cr) et la quantité d'électricité Q qui a traversé l'électrolyseur.
    - Calculer Q.
    - Quelle est la valeur de l'intensité du courant qui traverse la cuve à électrolyse pendant l'opération ?
    M(Cr) = 52 g/mol ; masse volumique du chrome r = 7,2 g/cm3.
corrigé
équation de la réaction d'électrode qui permet la formation du chrome métallique à partir des ions chrome III :

Cr3+(aq) + 3e- = Cr(s) , réduction à la cathode négative

volume de la couche de chrome à déposer :

surface du bloc : 2(L+l)h+2Ll = 2*210*0,5+2*200*10 =210+4000=4210 cm²

v= e *surface du bloc =50 10-4 * 4210= 21 cm3.

masse de chrome : r v = 7,2*21 = 151,6 g

Qté de matière (mol) : n(Cr) = m/M= 151,6/52 = 2,92 mol

donc d'après les coefficients de l'équation ci-dessus : n(e-) = 3 n(Cr) = 8,75 mol

quantité d'électricité Q qui a traversé l'électrolyseur : Q= 96500 n(e-) = 96500*8,75 = 8,44 105 C

de plus Q= It soit I = Q/t = 8,44 105 /(10*3600) = 23,4 A

en tenant compte du rendement électrolytique : 23,4/0,95 = 24,7 A.
retour -menu