Aurélie 04/06
d'après concours kiné Nantes 2006 (physique)

Google

Mesure du champ de pesanteur

Dans le repère (O i j k ) lié au sol on étudie le mouvement dans le vide d'un point matériel M de masse m ; l'axe Oz est vertical orienté vers le haut. A la date t=0, M est lancé verticalement vers le haut avec une vitesse initiale v0. Le champ de pesanteur g est uniforme. On note z son altitude à l'instant t ; il atteint l'altitude maximale zM à l'instant tM. Le but est la détermination précise de g.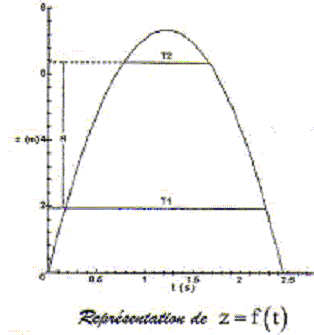

  1. Etablir les expressions de sa vitesse v et de son altitude z en fonction de g, v0 et t.
  2. Quelle est la vitesse à l'instant tM ? En déduire la relation entre v0, g et tM.
  3. Etablir la relation entre (zM-z), (t-tM), et g.
    - Exprimer la durée T qui sépare les dates de passage du mobile à une même altitude z en fonction de z, zM et g.
  4. On mesure les durées T1=2,100 s et T2 = 0,900 s entre les passages à deux stations d'altitude z1 et z2 telles que z2-z1=H= 4,415 m. Exprimer g en fonction de T1, T2 et H. Calculer g.
corrigé
expressions de sa vitesse v et de son altitude z en fonction de g, v0 et t :

axe vertical ascendant, origine au sol : v= -gt+v0 ; z=-½gt²+v0t.

vitesse à l'instant tM : au sommet de la trajectoire vertiale, la vitesse s'annule d'où la relation entre v0, g et tM : v0=gtM .

relation entre (zM-z), (t-tM), et g :

d'une part : z=-½gt²+v0t (1)

d'autre part : zM=-½gtM²+v0tM (2)

(2)-(1) donne : (zM-z) = -½g(tM²-t²) +v0(tM-t) = (tM-t)[ -½g(tM+t)+ v0)

remplacer v0 par g tM : (zM-z) = (tM-t)[ -½g(tM+t)+ g tM )

(zM-z) = (tM-t)[½g(tM-t)] d'où : (zM-z) = ½g(tM-t)2.

durée T qui sépare les dates de passage du mobile à une même altitude z en fonction de z, zM et g : T= 2(t-tM)

(zM-z)= ½g(T²/4) d'où T² = 8(zM-z)/g

Expression de g en fonction de T1, T2 et H :

T1² = 8(zM-z1)/g ; T2² = 8(zM-z2)/g ; T1² -T2² =8(z2-z1)/g = 8H/g ; g = 8H/(T1² -T2²)

g= 8*4,415/ (2,1²-0,9²)= 9,811 m/s².

régimes transitoires

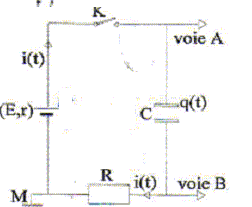
I- On considère que la pile a une résistance interne r négligeable.

A l'instant t=0, le condensateur est déchargé et on ferme l'interrupteur. On procède à l'enregistrement.

  1.  Que visualise-t-on sur la voie A.
  2. Etablir l'équation différentielle vérifiée par la charge q(t) de l'armature du condensateur.
  3. La solution de cette équation différentielle est de la forme q(t) = a+b exp(-t/t) où a, b et t sont des constantes.
    - Préciser la charge du condensateur à t=0 ; en déduire une relation entre a et b.
    - Déterminer a, b et t en fonction des paramètres du circuit.
  4. Etablir l'expression u(t) de la tension aux bornes du conducteur ohmique de résistance R.
  5. Donner l'allure des courbes observées sur les voies A et B avec des sensibilités identiques sur les deux voies.

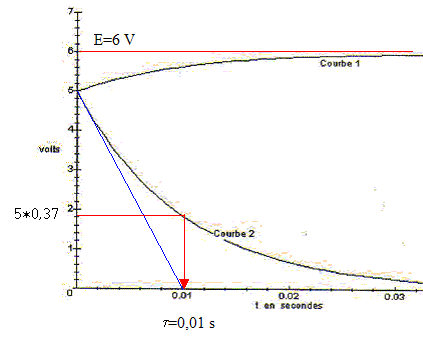
II- On considère que la pile a une résistance interne r non négligeable.

On obtient les deux courbes suivantes.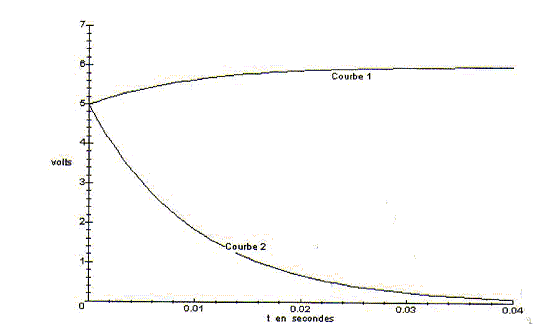

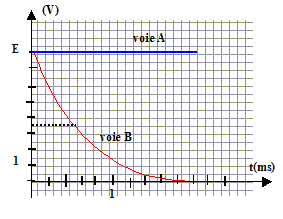
  1. Identifier les deux courbes. Donner la valeur de la fem de la pile E.
  2. Au début de la charge du condensateur (t=0) l'intensité du courant est I0. Déterminer I0 et r si R= 50 W.
    - Calculer la constante de temps t et en déduire la capacité C du condensateur.
  3. Calculer lorsque le régime permanent est atteint :
    - La charge Q du condensateur et l'énergie Ec stockée par ce dernier.
    - L'énergie totale EG fournie par le générateur.
    - L'énergie dissipée par effet joule dans R et dans r.
corrigé
sur la voie Aon visualise la tension aux bornes de la pile soit u=E.

équation différentielle vérifiée par la charge q(t) de l'armature du condensateur.

additivité des tensions aux bornes d'appareile en série : E= Ri + uC = Ri + q/C

or i= dq/dt = q' d'où : E= Rq' + q/C ou bien : q' + 1/(RC) q = E/R.

q(t) = a+b exp(-t/t) ; à t=0 la charge du condensateur est nulle soit 0= a+b

expressions de a, b et t en fonction des paramètres du circuit.

à t>>t la tension aux bornes du condensateur vaut E et qoo= CE d'où CE=a

q(t) = CE(1-exp(-t/t)) ; q' = CE/t exp(-t/t)

repport dans l'équation différentielle : CE/t exp(-t/t) +E/R (1-exp(-t/t))=E/R

relation vérifiée quel que soit t si t = RC.

expression u(t) de la tension aux bornes du conducteur ohmique de résistance R : u(t) = Ri(t)

avec i(t) = q' = E/Rexp(-t/t) ; u(t) =Eexp(-t/t)

allure des courbes observées sur les voies A et B avec des sensibilités identiques sur les deux voies.

Identifier les deux courbes : courbe 1 (tension aux bornes de la pile voie A) ; courbe 2 ( tension aux bornes deR voie B)

valeur de la fem de la pile E = 6V ; constante de temps t = 0,01 s ; C= t /R = 0,01/50 = 2 10-4 F

Au début de la charge du condensateur (t=0) l'intensité du courant est I0, le condensateur n'est pas chargé et la tension à ses bornes est nulle.

tension aux bornes du résistor = tension aux bornes de la pile = RI0 = 5 V ; I0 = 5/50 = 0,1 A.

Lorsque le régime permanent est atteint , charge Q du condensateur et énergie Ec stockée par ce dernier :

tension aux bornes du condensateur : E = 6V ; capacité C= 2 10-4 F

charge Q = CE = 2 10-4*6 = 1,2 10-3 C

énergie stockée par le condensateur Ec =½CE²= 0,5 * 2 10-4 *36 = 3,6 10-4 J.

L'énergie totale EG fournie par le générateur en régime permanent est nulle, car l'intensité du courant est nulle

L'énergie dissipée par effet joule dans R+r en régime permanent est nulle, car l'intensité du courant est nulle.

étude d'une loupe

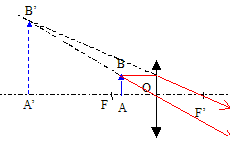
Une lentille convergente L, de distance focale 50 mm, est utilisée en loupe. On désire observer un objet AB de hauteur h= 2 mm avec cette loupe.

  1. Quelle est la vergence de cette lentille ?
  2. Où doit-on placer AB pour que son image se forme à l'infini ? Faire un schéma.
    - Sous quel angle qoo voit-on l'image de AB ?
    - Sous quel angle q0 verrait-on AB à l'oeil nu placé à la distance dm=25 cm ? En déduire le grossissement commercial de la loupe défini par GC= qoo/q0
  3. Déterminer la position et la taille de l'image quand l'objet AB est placé à 4,0 cm du centre optique O de la loupe. Faire un schéma à l'échelle.
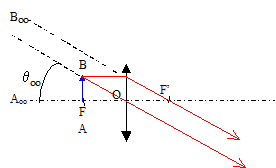
corrigé
vergence de cette lentille : 1/0,05 = 20 dioptries.

placer AB au foyer objet de la lentille pour que son image se forme à l'infini .

angle qoo sous lequel on voit l'image de AB : tan qoo = AB/OF = 2 10-3 / 50 10-3 = 0,04 d'où qoo =0,04 rad

angle q0 sous lequel AB à la distance dm=25 cm : tan q0 = 2 10-3 / 0,25 = 8 10-3 ; q0 = 8 10-3 rad

grossissement commercial de la loupe défini par GC= qoo/q0 = 0,04 / 0,008 = 5

position et la taille de l'image quand l'objet AB est placé à 4,0 cm du centre optique O :

 

mesure algébrique écrite en bleu et en gras

formule de conjugaison : 1/OF' = 1/OA' - 1/OA ; 1/OA' =1/OF' +1/OA = 20-1/0,04 = -5 ; OA' =-0,2 m

grandissement : OA' /OA = -0,2/(-0,04) = 5 ; taille de l'image : 5*2 = 10 mm
retour -menu