Aurélie 20/3/6
d'après concours interne d'ingénieur territorial 2005 Mécanique, électricité, énergétique

Google

Mécanique ( 4 pts).

On peut lire dans un documentation relative à une rame de TGV que celle-ci a une masse M=380 t à vide et 425 t en charge, une longueur L=200 m, une vitesse de croisière en palier (mouvement uniforme horizontal) v= 300 km/h ; alimentation 25kV-50Hz ; capacité : 516 places. On considère que le train roule sur un sol horizontal ; g = 9,8 m/s².

  1. Sachant que le train met 7 minutes pour passer de l'arrêt à sa vitesse de croisière, quelle est son accélération supposée constante, pendant cette phase ?
  2. Ce train de masse 420 t, passe sur un pont de 570 m de long alors qu'il roule à 300 km/h. Or ce pont fait un bruit caractéristique dès qu'une partie du train roule sur lui. Combien de temps dure ce bruit ?
  3. Toujours à la même vitesse, ce train aborde une courbe dont le rayon de courbure est de 6 km. Comme les passagers ne sont pas attirés vers les parois latérales des wagons pendant ce tournant, on demande de quel angle la voie est relevée.
  4. La puissance électrique consommée étant de 2000 kW en palier, les pertes thermiques et mécaniques dans la motrices étant estimées à 10 % de la puissance absorbée, en déduire l'intensité des forces de frottements opposées à l'avancement du train lorsqu'il roule à 300 km/h en palier.
corrigé
accélération a = Dv/Dt avec Dv en m/s et Dt en seconde.

Dv = 300 / 3,6 = 83,33 m/s ; Dt = 7*60 = 420 s ; a = 83,33/420=0,198 m/s².

durée du bruit : le bruit est audible dès que la motrice aborde le pont jusquà ce que le dernier wagon quitte le pont.

La distance parcourue par la motrice est donc : longueur du pont + longueur du train = 570+200=770 m.

vitesse du train : 300 / 3,6 = 83,33 m/s ; durée (s) = distance (m) / vitesse (m/s) = 770/83,33 = 9,2 s.

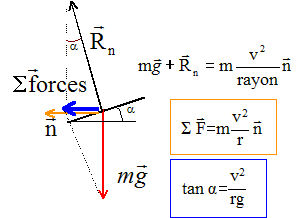
tan a = 83,332 / (6 103 *9,8) = 0,118 soit a = 6,7°.

Puissance( en valeur absolue) des frotttements : 200 kW

puissance d'une force = vecteur vitesse scalaire vecteur force

d'où 200 = v f soit f = 200 / 83,33 = 2,4 kN.

Electricité ( 3 pts)

Une installation fonctionnant sous 220 v - 50 Hz monophasé comprend :
- Un appareillage de puissance utile 29440 W, de rendement h=0,8 et de facteur de puissance cosj=0,75
- Un ensemble de 200 lampes de 100 W chacune.

La ligne qui alimente cette installation est équivalente au dipole série de caractéristiques : Rli=0,05 W ; Lli = 0,001 H et Cli = 12500 mF. On demande :

  1. L'intensité du courant dans la ligne.
  2. Le facteur de puissance de l'installation.
  3. Les pertes par effet joule dans la ligne.
  4. La puissance apparente au départ de la ligne.
  5. La tension au départ de la ligne.
  6. Le facteur de puissance au départ de la ligne.
corrigé
On note U : valeur efficace de la tension ; I : intensité efficace du courant ; P=UI cos j( watt) puissance active

S= UI, puissance apparente ( V A) et Q = UI sin j( var ) puissance réactive

La puissance consommée par l'appareillage vaut : Putile / rendement =29440 / 0,8 = 36800 W = 36,8 kW

Q est positif si l'appareillage est inductif ; négatif si l'appareillage est capacitif

P (watt)
S ( VA)
|Q |(var)
appareillage
36800
P/cosj=36800/0,75 = 49067
S sinj= 32455
lampes
20000
20000
0
total installation
56800
(56800²+32455²)½=65416
32455

intensité du courant dans la ligne : I= S/U =65416/220 =297 A.

facteur de puissance de l'installation : cosj= P/S = 56800/65416 =0,87.

pertes par effet joule dans la ligne : rI² =0,05*2972 = 4410 W.

fréquence : f = 50 Hz ; pulsation w= 2pf = 314 rad/s

réactance de la ligne X =Lw-1/(Cw) = 0,001*314 - 1/( 0,0125*314)=0,314-0,255 =0,059 W.

Puissance réactive de la ligne Qli =XI²=0,059*2972 = 5204 var.

Puissance réactive totale : Q=Qli + Qinst= 5204+32455 = 37660 var

Puissance active totale : P=Pli + Pinst= 4410+56800=61210 W

Puissance apparente au départ de la ligne : S= (P² + Q²)½ =(376602 + 612102)½=71867 VA.

tension au départ de la ligne : U= S/I =71867/297 = 242 V.

facteur de puissance au départ de la ligne : P/S =61210/71867= 0,85.

Energétique (3 pts)

On considère un mur de béton de 10 cm d'épaisseur qui sépare un milieu à 18°C d'un milieu à -20°C. La conductivité thermique du béton est l= 1,1 W m-1K-1. On adoptera h=8,12 W m-2K-1 pour tous les coefficients globaux de convection et rayonnement entre l'air et le béton.

  1. Calculer le flux thermique j par m2 de paroi.
  2. Le mur étant constitué de deux parois de béton de 5 cm d'épaisseur séparées par une couche d'air de 5 cm, calculer le nouveau flux j' et les températures dans le mur. On admettra que la transmission de chaleur dans la couche d'air se fait uniquement par convection et rayonnement.
corrigé
résistance thermique du mur : R= e/l + 1/h ; e : épaisseur du béton

résistance thermique de l'ensemble : résistance thermique du béton + résistance due à la convection et rayonnement de chaque côté de la paroi en béton.

R= 0,1/1,1 + 2/8,12 = 0,337 W-1 m2 K.

coefficient de transmission : K= 1/R = 1/0,337 = 2,96 Wm-2K-1.

flux thermique surfacique : F= K(qc-qf) = 2,96(18+20)= 113 W m-2.

résistance thermique de l'ensemble : résistance thermique du béton + résistance due à la convection et rayonnement de chaque côté de la paroi en béton + résistance thermique due à la convection et rayonnement dans l'air interne.

résistance thermique du mur : R'= e/l + 3/h ; e : épaisseur du béton

R'= 0,1/1,1 + 3/8,12 = 0,46 W-1 m2 K.

coefficient de transmission : K'= 1/R'= 1/0,46 = 2,17 Wm-2K-1.

flux thermique surfacique : F'= K'(qc-qf) = 2,17 (18+20) = 82,5 W m-2.

températures internes du mur :

R1 = 1/h +e1/l =1/8,12 +0,05/1,1 =0,169 ; K1 = 1/0,169 =5,93 ; (qc-q1) = F'/K1 =82,5/5,93 = 13,9 d'où q1 = 18-13,9 = 4,1°C.

même calcul à partir de l'extérieur :

R1 = 1/h +e1/l =1/8,12 +0,05/1,1 =0,169 ; K1 = 1/0,169 =5,93 ; (q2-qf) = F'/K1 = 82,5/5,93 = 13,9 d'où q2 = 13,9-20 = - 6,1°C.
retour -menu