|
|
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
Un joueur de tennis ( joueur 1) désire effectuer un lob, cela signifie qu'il doit envoyer la balle suffisamment haut pour que son adversaire ( joueur 2) ne puisse pas l'intercepter. La balle doit retomber dans les limites du court. On notera A le point où le joueur 1 frappe la balle, O comme origine du repère. OA= z0 = 1,00 m, ordonnée de A ; z1 = 3,00 m ordonnée correspondant à la hauteur maximale pour laquelle le joueur 2 peut intercepter la balle quand il lève sa raquette. x1 = 15,0 m, abscisse correspondant à la position du joueur 2.; x2 = 25,0 m , abscisse correspondant à la ligne de fond du court du joueur 2. v0 vitesse initiale de la balle en A ; a= 45,0° ; g=9,80. 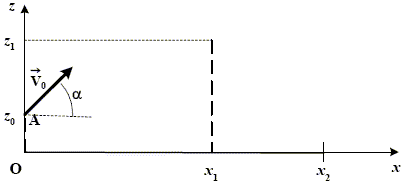 Pour que le lob soit réussi, il faut donc que la balle issue de A avec la vitesse initiale v0 soit telle que z>z1 pour x=x1 et que x<x2 pour z=0. On se propose se déterminer les valeurs de la vitesse initiale v0 pour que le lob soit réussi. On néglige tous les effets liés à l’air.
corrigé nom mathématique de la courbe décrite par la trajectoire de la balle : arc de parabole expressions littérales des composantes du vecteur vitesse initiale : sur Ox : v0x= v0 cos a ; sur Oz : v0z = v0 sin a. expressions littérales des équations horaires x(t) et z(t) : composantes de l'accélération : ax=-g ; az=0 ; position initiale : x0 = 0 ; z0 = OA la vitesse est une primitive de l'accélération : vx= v0x= v0 cos a ; vy = -gt +v0 sin a. Le vecteur position est une primitive deu vecteur vitesse : x= v0 cos a t ; z = -½gt² + v0 sin a t + z0 . expression littérale de la trajectoire z(x) : t =x/( v0 cos a ) ; repport dans z : z= -½gx²/( v0 cos a )² + x tan a + z0. expression de vitesse initiale v0
en fonction de x, z, z0, a
et g : v0 = [ ½gx² /((-z+ z0 +x tan a)cos² a)]½. valeur numérique v0 1 de la vitesse initiale pour que la balle touche le sol au point de coordonnées : x = x1 z = z1 : v0 1 =[ ½gx1² /((-z1+ z0 +x1 tan a)cos² a)]½ = [4,9*15²/((-3+1+15)*0,5]½ =[4,9*225/6,5]½ =13,0 m/s. valeur numérique v0 2 de la vitesse initiale pour que la balle touche le sol au point de coordonnées : x = x2 z = 0 : v0 2 =[ ½gx2² /((-z2+ z0 +x2 tan a)cos² a)]½ = [4,9*25²/((1+25)*0,5]½ =[4,9*625/13]½ =15,3 m/s. intervalle de la valeur de la vitesse initiale pour lequel le lob est réussi : [13,0 ; 15,3 m/s]
|
|||||||||||||||||||||||||||||||
|
La TEP tomographie par émission de positons (ou positron) est une technologie de médecine nucléaire qui utilise des molécules marquées avec un isotope émetteur de positons pour imager le fonctionnement ou le dysfonctionnement d’organismes vivants. On utilise principalement le fluorodesoxyglucose FDG marqué au fluor 18 pour ce type d’examen.
corrigé réaction nucléaire correspondant à la formation de 189F : 188O + 11H ---> 189F + 10n (fluor 18 et neutron) composition du noyau de fluor 18 : 9 protons et 18-9 = 9 neutrons. réaction nucléaire de désintégration b+ du fluor 18 : 189F ---> AZX + 01e conservation de la charge : 9=Z+1 soit Z=8 ; conservation du nombre de nucléons : 18=A+0 ; ( 188O et positon) constante radioactive l du fluor 18 : l t½=ln2 soit l = ln2 / t½ = ln2/(110*60) = 1,05 10-4 s-1=6,30 10-3 min-1. nombre de noyaux de fluor 18 reçu : A=l N soit N= A/l = 3 108 / 1,05 10-4 =2,86 1012 . heure de départ de la salle d’examen : A= A0 exp(-lt) avec A/A0 = 0,01 et l= 6,30 10-3 min-1. t = ln(0,01) / (-6,30 10-3 )= 731 min ou 12 h 11 min ; sortie à 10 h + 12 h 11 = 22 h 11 min équation de la réaction d’annihilation du positon : 01e + 0-1e = 2 00g. énergie en MeV de chacun des photons : Etotale = 2mec² 9,1 10-31 *(3 108)² =8,19 10-14 J ; 8,19 10-14 /1,6 10-19 = 5,12 105 eV = 0,51 MeV pourcentage de rayonnement transmis à l’extérieur : 5 cm = 50 mm ; 50 / 4 = 12,5 4 mm de protection : il reste 0,5= 1/2 *100 rayonnement émis 8 mm de protection : il reste 0,5*0,5=0,25 = 1/2² *100 rayonnement émis 12 mm de protection : il reste 0,5*0,5*0,5=0,125 = 1/23 *100 rayonnement émis d'où : 100 * 1/212,5 = 1,7 10-2 %.
|
|||||||||||||||||||||||||||||||
|
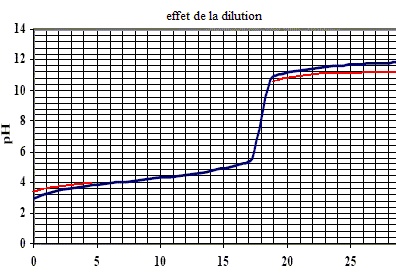
L’acide benzoïque, de formule semi-développée C6H5COOH, est utilisé comme conservateur dans l’industrie alimentaire. On le notera dans l’exercice AH. On peut déterminer la concentration d’une solution S d’acide benzoïque en menant un dosage acide-base par une solution d’hydroxyde de sodium (soude) fraîchement préparée, de concentration connue : [NaOH] = 0,05 mol.L-1. Pour ce faire, on prélève à l’aide d’une pipette graduée 50,0 mL d’une solution d’acide benzoïque, que l’on verse dans un bécher. Après avoir équipé ce dernier d’un système d’agitation et d’un pH-mètre, on introduit progressivement la solution de soude à l’aide d’une burette graduée et on porte la valeur indiquée par le pH-mètre en fonction du volume de soude ajouté. 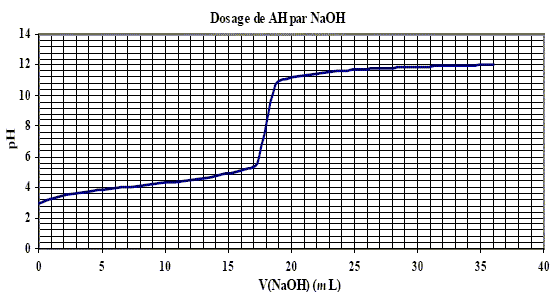
corrigé pH de la solution titrante de soude : pH= 14 + log c = 14 + log 0,05 = 12,7. équation de la réaction de dosage : C6H5COOH + HO- = C6H5COO- + H2O ; K= [C6H5COO- ]/([C6H5COOH][HO-]) pKa du couple AH/A- : à la demi équivalence du dosage, pH=pKa soit pKa = 4,2 ( lecture graphe à V=½Véq = 9 mL). constante d’équilibre de la réaction de dosage : C6H5COOH + H2O = H3O+ + C6H5COO- ; Ka =[C6H5COO-][H3O+]/[C6H5COOH] soit [C6H5COO-]/[C6H5COOH] = Ka / [H3O+] repport dans K : K= Ka/([HO-][H3O+]) = Ka/Ke = 10-4,2 / 10-14 = 109,8 . La réaction est rapide, totale et exothermique. pH à l’équivalence : présence de la base ion benzoate, donc pH basique ( le graphe indique pHéq=7,6). le meilleur indicateur coloré pour ce dosage : le pH éq doit appartenir à la zone de virage de l'indicateur coloré, donc rouge de crésol. concentration en acide benzoïque de la solution S : [à l'équivalence, [NaOH] Véq = CaVa soit Ca = [NaOH] Véq / Va= 0,05*18/50 = 1,8 10-2 mol/L concentration en g.L-1 d’acide benzoïque = concentration molaire * masse molaire 1,8 10-2 * (7*12+6+32) = 2,2 g/L.
|
|||||||||||||||||||||||||||||||
|
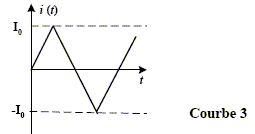
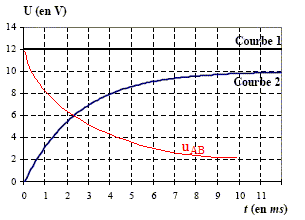
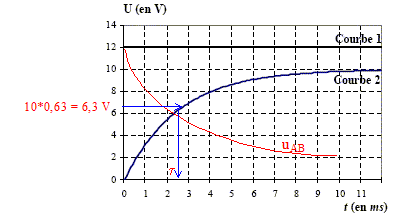
Un dipôle est constitué de l’association en série d’une bobine présentant une inductance L et une résistance RL avec un conducteur ohmique de résistance R=40 W. Ce dipôle est alimenté par un générateur de tension de f.é.m. E à travers un interrupteur K. Il est parcouru par un courant i. Les bornes A, B, et C sont reliées aux entrées d’une carte d’acquisition permettant d’enregistrer l’évolution des tensions. A l’instant t = 0, on ferme l’interrupteur K, l’enregistrement génère les courbes 1 et 2. 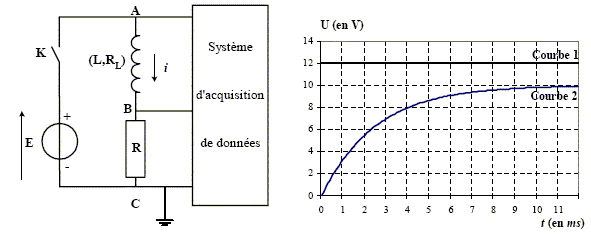
corrigé tension est représentée par la courbe 1 : uAC=E tension est représentée par la courbe 2 : uBC=Ri allure de la courbe de variation du courant i choisie parmi les quatre courbes ci-dessous : III allure de la courbe de variation de la tension uAB = uAC+uCB=uAC-uBC= E-uBC en régime permanent uAB =RLIMax = 8*0,25 = 2 V
valeur E et l’intensité maximale IMAX atteinte par i : E= 12 V ( lecture graphe) RIMax = 10 V soit IMax =10/R=10/40 = 0,25 A équation différentielle définissant i : E= Ldi/dt + RL i + Ri ; Ldi/dt + (RL + R)i = E en régime permanent i=IMax= constante et dIMax/dt=0 d'où E= (RL+R)IMax RL= E/IMax-R= 12/0,25-40 = 8 W. valeur de L : t = L/(RL+R) = 2,5 10-3 s soit L= t (RL+R) =2,5 10-3*48 = 0,12 H
allure de la courbe de variation de la tension uAB et de la courbe de variation de la tension uBC uAB = Ldi/dt avec i fonction affine par intervalle donc di/dt = fonction constante par intervalle : courbe V uBC et i sont proportionnelles : courbe VIII
|
|||||||||||||||||||||||||||||||
|
|