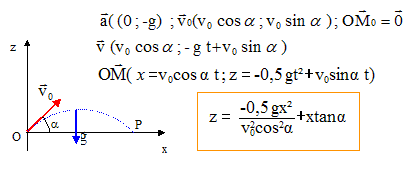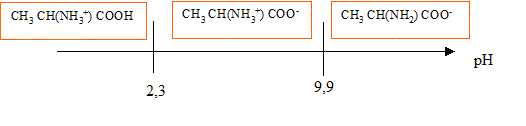Aurélie 21/12/05
 

Projectile; dipole LC, acide base, alanine, ammoniac, méthylamine

d'après concours controleur de la concurence et de la répression des fraudes 2004

Google

Mouvement d'un projectile ( 15 pts).

Un homme étudie le mouvement d.un projectile de centre de gravité G et de masse m, dans un champ uniforme de pesanteur terrestre. Le sol est horizontal. Les forces de frottements sont considérées comme négligeables ainsi que la poussée d.Archimède.

Soit un repère du référentiel terrestre tel que l'origine O coïncide avec la position du projectile à l'instant t = 0 du lancement. L'axe vertical orienté vers le haut et le plan (x O z) contient le vecteur vitesse initiale V0 qui fait un angle a avec l'axe horizontal.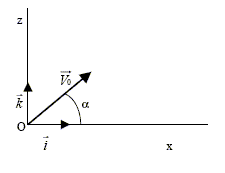

  1.  
  2. Faire le bilan des forces s'exerçant sur le projectile.
  3. Etablir les équations horaires paramètriques du mouvement.
  4. Le mouvement est-il plan ? Justifier.
  5. Sur quel axe le mouvement est-il uniforme ?
  6. Quelle est l'équation de la trajectoire ?
  7. A quelle distance de O le projectile tombe-t-il sur le sol ?
  8. Pour quelle valeur de a cette distance est-elle maximale ?
corrigé
chute libre : la balle n'est soumise qu'à son poids, vertical, vers le bas, valeur mg.

Ecrire la seconde loi de Newton

la vitesse est une primitive de l'accélération ; la position est une primitive de la vitesse.

y=0 : le mouvement s'effectue dans le plan vertical défini par les vecteurs accélération et vitesse initiale.

Sur l'axe Ox, la composante du vecteur vitesse est constante, égale à v0 cos a : le mouvement est uniforme sur l'axe Ox horizontal.

En retombant sur le sol z = 0 soit : -0,5 g x² / (v0²cos²a) + x sin a /cos a =0

multiplier par cos a et diviser par x : -0,5 g x / (v0²cosa) + sin a =0

0,5 gx = v0²cosa sin a ; x = 2 v0²cosa sin a / g = v0² sin (2a) / g

cette distance est maximale si sin (2a) = 1 soit a = 45°.

Circuit LC (15 pts)

Un condensateur de capacité C= 20 mF chargé sous une tension U= 5 V est branché aux bornes d'une bobine d'inductance L = 50 mH.

  1. Faire le schéma du montage en représentant la tension uc aux bornes du condensateur, les charges sur les armatures et l'intensité du courant dans le circuit.
  2. Les oscillations sont-elles libres ou forcées ? Justifier.
  3. Montrer que l'équation caractéristique du circuit est : d²q/dt² + q / (LC) = 0
  4. Quelle est la pulsation propre du circuit ? Préciser son unité.
  5. Calculer la valeur de la période propre du circuit.
  6. Vérifier que la tension aux bornes du condensateur peut s'écrire uc = U cos(w0 t).
  7. Préciser les conditions initiales.
  8. Calculer l'énergie totale du circuit à l'instant t. Montrer qu'elle est indépendante du temps.
corrigé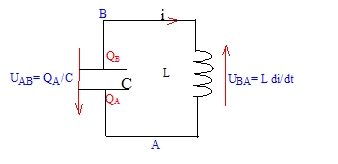

L'armature QA porte une charge négative ; QB= -QA. uc = UAB

Les oscillations sont-elles libres ; aucun générateur n'est présent : ce dernier forcerait le circuit (LC)à osciller à la fréquence du générateur.

UAB + UBA=0 ; QA/C + Ldi/dt = 0 ; i = dQA/dt ; di/dt =d²QA/dt²

d'où : QA/C + Ld²QA/dt² = 0 soit : d²QA/dt² +QA/ (LC ) = 0

La pulsation propre w0 s'exprime en radian/seconde ; sa valeur est telle que w02 = 1/(LC) = 1/( 0,05*2 10-5) = 106.

w0 = racine carrée (106) = 103 rad/s.

période propre : T0 = 2p /w0 =6,28 / 103 =6,28 10-3 s.

uc = U cos(w0 t ); QA = C UAB = C U cos(w0 t)

dériver deux fois par rapport au temps : dQA /dt = -w0C U sin(w0 t) ; d²QA /dt² = -w²0C U cos(w0 t) ;

repport dans l'équation différentielle : d²QA/dt² +QA/ (LC ) = 0 avec w02 = 1/(LC)

-w²0C U cos(w0 t) + C U/ (LC) cos(w0 t) = 0 est vérifiée quelle que soit le temps

Donc uc = U cos(w0 t ) représente la tension aux bornes du condensateur

à t=0 le condensateur est chargé et la tension à ces bornes vaut : Umax = 5 V d'où uc = 5 cos(w0 t )

L'énergie initiale du dipole (LC) est stockée par le condensateur et vaut : E=½CU² = 0,5*20 10-6 *25 = 6,25 10-4 J

Au cours du temps il y a échange d'énergie entre condensateur et bobine inductive.

E= ½Li²(t) + ½Cu²c(t)

Si la résistance du circuit est nulle, l'énergie se conserve.

Chimie

Données : N( Z=7) ; H (Z=1) ;

masse atomique mlolaire (g/mol) : N : 14 ; H : 1.

constante d'acidité : NH4+/NH3 : pKa = 9,2 ; CH3NH3+ / CH3NH2 : pKa = 10,75 ; alanine : pKa1 = 2,3 et pKa2 = 9,9.
Indicateurs colorés
zone de virage
phénolphtaléine
8,3 - 10,0
bleu de bromothymol
6,0 - 7,3
rouge de méthyle
4,2 - 6,3
hélianthine
3,4 - 4,4
Conductivité molaire ionique mS m² mol-1.
nature de l'ion
H3O+
NH4+
HO-
Cl-
l
34,98
7,34
19,92
7,63

  1. Donner la configuration électronique de l’atome d’hydrogène et de l’atome d’azote.
  2. Indiquer la nature des liaisons dans la molécule d’ammoniac (NH3) et la géométrie de cette molécule en utilisant la méthode VSEPR (en particulier préciser, en justifiant votre réponse, l’ordre de grandeur des angles des liaisons azote-hydrogène).
  3. Dosage pH-métrique : on se propose de réaliser le dosage de 100 mL d’une solution aqueuse de NH3 de concentration C par une solution d.acide chlorhydrique de concentration 1,100 mol.L-1. Le volume équivalent, noté veq est de 8,00 mL.
    - Quelles sont les électrodes nécessaires à ce dosage et indiquer leur rôle ?
    - Écrire l’équation bilan de la réaction de dosage et déterminer la concentration C de la solution ammoniacale.
    - Quelle est la nature de la solution à l’équivalence ? Calculer le pH à l’équivalence et proposer un indicateur coloré qui permettrait de réaliser ce dosage par colorimétrie.
    - Calculer la concentration de la solution commerciale de densité 0,88 et dont le pourcentage en masse d’ammoniac est de 32 %.
  4. Dosage conductimétrique : on réalise le même dosage que précédemment mais il est suivi maintenant par conductimétrie. On supposera que la dilution est négligeable. Donner l’allure de la courbe obtenue en traçant la conductance G en fonction du volume V d’acide chlorhydrique versé. On indiquera sur chaque portion de droite, la nature des entités responsables de la variation de la conductivité.
corrigé
configuration électronique de l’atome d’hydrogène : K1

de l’atome d’azote : K2L5.

nature des liaisons dans la molécule d’ammoniac : covalente polarisée, l'atome d'azote attire à lui le doublet de liaison.

géométrie de cette molécule : pyramide à base triangulaire, l'atome dazote est au sommet de la pyramide et porte un doublet non liant ( type AX3 Ed ans la méthode VSEPR)

angle HNH : 107 °, inférieur à 109° car le doublet non liant repousse les trois doublets liants.

électrode combinée de pH intégrant une sonde de température

équation bilan de la réaction de dosage : NH3 + H3O+ = NH4+ + H2O

à l'équivalence du dosage, les quantités de matière des réactifs sont en proportions stoéchiométriques :

n(NH3) = 100 C ; n(H3O+) = 1,1*8 = 8,8

C= 8,8 / 100 = 8,80 10-2 mol/L

nature de la solution à l’équivalence : chlorure d'ammonium NH4+ ; Cl-.

le pH à l’équivalence : [H3O+]²= Ka C ; 2 log [H3O+] = log Ka + log C ; pH = ½(pKa-log C)

pH= 0,5 (9,2-log (8,80 10-2 ) = 5,1.

le pH à l'équivalence doit appartenir à la zone de virage de l'indicateur coloré : rouge de méthyle

concentration de la solution commerciale de densité 0,88 et dont le pourcentage en masse d’ammoniac est de 32 % :

masse de 1 L de solution : 880 g ; masse d'ammoniac pure : 880*0,32 =281,6 g

masse molaire ammoniac : 14+3 = 17 g/mol

concentration : 281,6 / 17 = 16,5 mol/L.

Dosage conductimétrique :

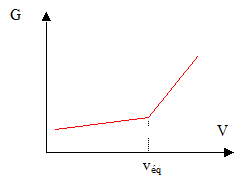
avant l'équivalence, dans l'erlenmeyer , l'acide est en défaut : les molécules d'ammoniac réagissent avec les ions oxonium ajoutés ; on ajoute des ions chlorure et il se forme des ions ammonium. Seuls les ions contribuent à la conductivité de la solution : tout se passe, du point de vue de la conductivité comme si on remplaçait des molécules NH3 par des ions NH4+ et Cl-. La conductivité de ces ions n'est pas très grande ( comparée à celle de l'ion oxonium) : la conductivité de la solution augmente lentement. Conductance et conductivité étant proportionnelles, la conductance augmente lentement.

après l'équivalence, dans l'erlenmeyer , l'acide est en excès : on ajoute des ions H3O+ et Cl-. La conductivité de l'ion oxonium étant 5 fois plus grande que celle des ions Cl- et NH4+, la conductivité, donc la conductance augmente fortement.
ammoniac et méthylamine

On considère les deux composés, ammoniac et méthylamine.

  1. Donner la formule développée de la molécule de méthylamine. À quelle famille appartient ce composé ?
  2. Écrire la réaction sur l’eau de ces deux composés. En déduire le caractère acidobasique de ces composés.
  3. On mesure le pH des solutions aqueuses d’ammoniac et de méthylamine de concentrations molaires égales à 0,10 mol.L-1. On obtient les résultats suivants : Ammoniac pH=11,1 ; Méthylamine pH= 11,9. Calculer le taux de protonation a de ces deux composés dans les solutions aqueuses. Le taux de protonation a est le rapport du nombre de moles protonées sur le nombre de moles à l’instant initial.
    - Comparer la force du caractère acidobasique de ces deux composés.

 

corrigé
formule semi développée de la molécule de méthylamine : CH3-NH2 amine primaire

NH3 + H2O = NH4++HO-avec [NH4+]= [HO-] = 10-14/[H3O+] = 10-14/10-11,1 = 10-2,9

CH3-NH2 + H2O = CH3NH3+ + HO- avec [CH3NH3+]= [HO-] = 10-14/[H3O+] = 10-14/10-11,9 = 10-2,1

Ces molécules sont des bases : on observe l'apparition d'ion hydroxyde en solution.

taux de protonation a = [NH4+] / C = 10-2,9/0,1 = 10-1,9 = 1,25 10-2 ( 1,25 %)

a = [CH3NH3+] / C = 10-2,1/0,1 = 10-1,1 = 8 10-2 ( 8 %)

Comparer la force du caractère acidobasique de ces deux composés :

le taux de protonation est plus grand pour la méthylamine : celle ci est une base plus forte que l'ammoniac à concentration égale.
Étude d'un acide aminé : l'alanine

L’alanine a pour formule chimique CH3 CH(NH2) COOH. Ce composé existe à l’état solide et en solution aqueuse sous la forme d’un amphion ou ion dipolaire ou zwittérion de formule chimique CH3 CH(NH3+) COO-.

  1. Expliquer la présence de cet ion.
  2. Quelle est la base conjuguée de l’amphion ?
  3. Quelle est la formule de l’acide conjugué de l’amphion ?
  4. L’amphion intervient dans 2 couples acide / base, attribuer à chaque couple sa constante d’acidité en justifiant votre réponse.
  5. Établir le domaine de prédominance de chaque espèce intervenant dans les 2 couples acide / base (cités en 4).
  6. Calculer à 25°C le pH d’une solution d’alanine de concentration 0,1 mol.L-1.
corrigé
Dans la molécule d'alanine on trouve deux fonctions chimiques : une fonction amine -NH2 au caractère basique et une fonction acide carboxylique, au caractère acide. Base conjuguée de l’amphion : CH3 CH(NH2) COO- ; acide conjugué de l’amphion : CH3 CH(NH3+) COOH

Les couples acide base sont :

CH3 CH(NH3+) COOH / CH3 CH(NH3+) COO- pKa1 = 2,3

CH3 CH(NH3+) COO- / CH3 CH(NH2) COO- pKa2 = 9,9.

Lorsqu'on dissout de l'alanine dans l'eau, elle est essentiellement sous forme d'ion dipolaire -OOC-RCH-NH3+,( du fait de la forte solubilité dans l'eau) la concentration en molécules HOOC-RCH-NH2 est négligeable.

HOOC-RCH-NH3+ + H2O = -OOC-RCH-NH3+ + H3O+ pKa1= 2,3
-OOC-RCH-NH3+ + H2O = -OOC-RCH-NH2 + H3O+ pKa2 = 9,9
On note AH+ : HOOC-RCH-NH3+ ; A : -OOC-RCH-NH3+ ; A- : -OOC-RCH-NH2 et [H3O+] : h

AH+ + H2O = A+ H3O+ ; Ka1 = [A] h / [AH+] = 10-2,3 = 0,005.

A + H2O = A- + H3O+ ; Ka2 = [A-]h / [A]= 10-9,9 = 1,25 10-10

conservation A : [AH+]+[A]+[A-]=0,1 ; or A majoritaire dans l'eau : [A] voisin 0,1 mol/L

solution électriquement neutre : h+ [AH+] = [OH-]+[A-]

hypothèse : h et [OH-] négligeable devant [AH+] et [A-] alors [AH+] =[A-]

Ka1 * Ka2 = h²[A-] / [AH+] = 6,25 10-13

h²= 6,25 10-13 ; pH= 6,1.

si on calcule [AH+] et [A-] on trouve : [AH+] = [A] h/Ka1 = 0,1 * 10-6,1 / 0,005 = 1,6 10-5 alors que h= 7,8 10-7

[A-] =Ka2[A]/h= 1,25 10-10*0,1/ 10-6,1 = 1,6 10-5 ; hypothèse confirmée
retour -menu