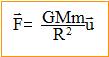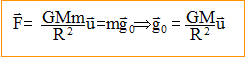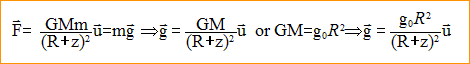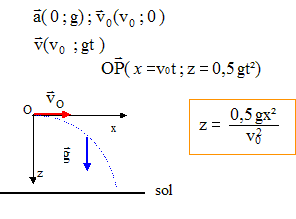
Chute libre, champ de gravitation, dosage acide iodique, indice d'iode des corps gras, acétate de butyle d'après concours controleur de la concurence et de la répression des fraudes 2002

Aurélie 3/3/06

Chute libre

I. Citer : le principe d'inertie, la loi des actions réciproques, le théorème du centre d'inertie, le théorème de l'énergie cinétique ( 2pts)

II. Chute libre (5 pts)

Soit un solide dense de petites dimensions (une bille par exemple) de masse m = 20 g. Nous étudions la chute dans le référentiel terrestre considéré comme galiléen auquel nous lions le repère orthonormé (O, i, j, k). Le sol est situé à 0,80 m au-dessous du point O. On lâche (ou on lance ) le corps du point O, à une

date choisie comme origine des dates. On néglige la résistance de l'air et on prend g =10 ms^{- 2} . Le champ de pesanteur est considéré comme uniforme dans le domaine de l'espace où évolue le solide.

Chute libre sans vitesse initiale : le corps est lâché sans vitesse initiale.
- Écrire l'équation horaire du mouvement.
- Calculer le temps mis par le corps pour atteindre le sol.
- Calculer la vitesse du corps quand il atteint le sol.
Chute libre avec vitesse initiale verticale vers le haut : le corps est maintenant lancé verticalement vers le haut avec une vitesse initiale v₀= 3,0 m/s.
- Calculer la vitesse du corps quand il atteint le sol.
- Calculer le temps mis par le corps pour atteindre le sol.
Chute libre avec vitesse initiale horizontale dirigée suivant l'axe Ox. Le corps est ensuite lancé horizontalement suivant l'axe Ox dans le sens positif, avec une vitesse initiale v₀= 3,0 m/s
- Écrire les équations horaires des mouvements suivant les axes Ox et Oz .
- En déduire l'équation cartésienne de la trajectoire.

corrigé

principe d'inertie : dans un référentiel galiléen, si la somme vectorielle des forces extérieures appliquées à un solide est nulle ( solide pseudo-isolé ) alors le centre d’inertie G de ce solide est soit au repos, soit animé d'un mouvement rectiligne uniforme et réciproquement.

théorème du centre d'inertie : dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie.

interaction entre un objet A et un objet B : (loi des actions réciproques) si un solide noté A exerce sur un solide noté B une force notée F _{A
/ B}, alors B exerce sur A une force notée F_{B / A} . Les deux forces associées à une même interaction sont toujours égales et opposées.

théorème de l'énergie cinétique : dans un référentiel galiléen, pour un solide ponctuel de masse m, lors d'un déplacement reliant un point A à un point B, la variation d’énergie cinétique est égale à la somme des travaux des forces extérieures qui s’exercent sur le solide.

Chute libre sans vitesse initiale : axe Oz vertical vers le bas, origine O: le point de départ

équation horaire : z=½gt² = 5 t²

temps mis par le corps pour atteindre le sol : t= racine carrée ( z/5) = racine carrée (0,8/5) = 0,4 s.

vitesse du corps quand il atteint le sol : v= gt = 10 t = 10*0,4 = 4 m/s.

Chute libre avec vitesse initiale verticale vers le haut : axe Oz vertical vers le bas, origine O: le point de départ

vitesse du corps quand il atteint le sol : v = gt -v₀= 10t-3 et z = ½gt²-v₀t = 5t²-3t

éliminer le temps entre ces deux équations : t=0,1(v+3) ; z = 0,05 (v+3)²-0,3(v+3)

changement de variable : V= v+3 ; z = 0,05 V²-0,3 V

au sol z= 0,8 ; résoudre : 0,05 V² -0,3 V-0,8 = 0 ; V= 8 soit v= 5 m/s.

temps mis par le corps pour atteindre le sol : v = 10 t-3 ; au sol v= 5 m/s ; t= (5+3) / 10 = 0,8 s.

Chute libre avec vitesse initiale horizontale :

Champ de gravitation (3 pts)

Soient deux corps ponctuels placés en A et B, de masses respectives m_A et m_B , séparés par une distance AB. Exprimer la loi de gravitation universelle sous forme vectorielle. Faire un schéma.
On suppose que la Terre est exactement sphérique, de rayon R, de masse M et qu'elle possède une répartition des masses à symétrie sphérique.
- Donner l'expression vectorielle de la force exercée par la Terre sur un solide de masse m, considéré comme ponctuel et situé à sa surface.
- En déduire l'expression vectorielle du champ de gravitation g₀ de la Terre à l'altitude z=0 m.
- Sachant que m = 1 kg, calculer la valeur de M.
- Constante de gravitation: G= 6,67 10^{- 11} S.I. ; Rayon de la Terre: R = 6400 km ; Champ de gravitation g₀= 9,8 N/kg
- Montrer qu'à l'altitude z au-dessus de la Terre, le champ de gravitation g est donné par la relation g= g₀R²/(R+z)²

corrigé

L'interaction gravitationnelle (Newton 1867) entre les masses.

Deux corps A et B de masses respectives m_A et m_B séparés d'une distance d exercent l'un sur l'autre des forces opposées attractives, importantes dans l'infiniment grand, négligeables dans l'infiniment petit.

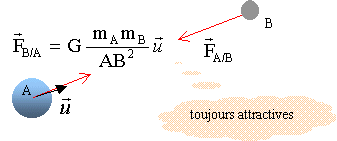
expression vectorielle de la force centripète exercée par la Terre sur un solide de masse m, considéré comme ponctuel et situé à sa surface :

expression vectorielle du champ de gravitation g₀ de la Terre à l'altitude z=0 m :

M= g₀R²/G = 9,8 *(6,4 10⁶)²/ 6,67 10^-11 = 6 10²⁴ kg

l'altitude z au-dessus de la Terre :

acide iodique (5 pts)

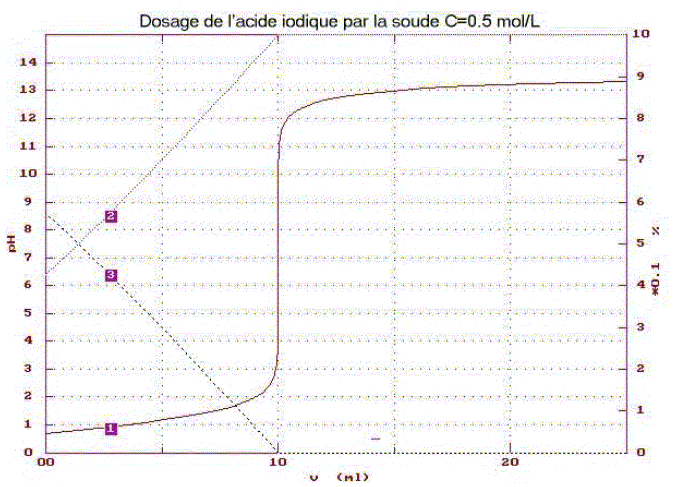
L’acide iodique HIO₃ est un monoacide faible, dont la base conjuguée est l’ion iodate.

Donner la définition d’un acide et d'une base d’après BRÖNSTED et donner la formule chimique de l’ion iodate.
On se propose de doser l’acide iodique par une solution d’hydroxyde de sodium ou (soude) de concentration molaire égale à c_b=0,500 mol/L. La solution titrante de soude est placée dans une burette de 25,0 mL. Dans un bécher on place E = 10,0 mL de solution d’acide à titrer et des électrodes reliées à un pHmètre.
Donner le nom et le rôle de chaque électrode utilisé.
La courbe de simulation du dosage est donnée ci-dessous :
Identifier les tracés 1; 2; 3 et déterminer les coordonnées V_e et pH_e à l'équivalence.
- Définir la constante d’acidité du couple acido-basique étudié et donner sa valeur en utilisant la courbe de simulation ci-dessus.
- Écrire l’équation de la réaction du dosage. Calculer la constante d'équilibre et conclure.
- En déduire la concentration C_a de l’acide iodique dosé.
- D'après les calculs précédents, justifier l'ordre de grandeur du pH_e équivalent et l'allure du tracé 1.

corrigé

définition d’un acide : espèce ion ou molécule susceptible de céder un proton H⁺.

définition d’une base : espèce ion ou molécule susceptible de gagner un proton H⁺.

ion iodate IO₃^-.

électrode combinée de pH intégrant une sonde de température

Identifier les tracés 1 ; 2; 3 :

1 : courbe du dosage pH= f(volume de soude ajouté)

3 : fraction molaire de HIO₃ ; 2 : fraction molaire IO₃^-.

L'ordonnée de l'intersection des courbes 2 et 3 donne le pH à l'équivalence : pH_e = 7,5 ; l'abscisse de l'intersection de la courbe 2 avec l'axe horizontal donne le volume de soude ajouté à l'équivalence V_e= 10 mL.

constante d'acidité K_a: HIO₃ + H₂O = IO₃^- + H₃O⁺.

K_a = [IO₃^-][H₃O⁺] / [HIO₃]

Le pH à la demi-équivalence donne la valeur du pK_a soit pK_a = 1,2 ( lecture graphe) : K_a = 10^-1,2 = 6,3 10^-2.

équation de la réaction du dosage : HIO₃ +HO^- = H₂O + IO₃^-

K= [IO₃^-]/([HIO₃][HO^-]) avec [IO₃^-]/[HIO₃] = K_a /[H₃O⁺]

K= K_a /([H₃O⁺][HO^-]) = K_a / K_e = 6,3 10^-2 / 10^-14 = 6,3 10¹².

cette valeur étant très grande, la transformation est totale

concentration C_a de l’acide iodique :

à l'équivalence les quantités de matière des réactifs sont en proportions stoéchiomètriques

C_aV_a = C_b V_e soit C_a = C_b V_e / V_a = 0,5*10 /10 = 0,500 mol/L

ordre de grandeur du pH_e :

conservation élément iode : [IO₃^-]_é + [HIO₃]_é = C_a --> [IO₃^-]_é voisin C_a

solution élecriquement neutre : [IO₃^-]_é +[HO^-]_é =[ H₃O⁺]_é +[Na⁺]_é

[ H₃O⁺]_é négligeable devant [HO^-]_éet [Na⁺]_é=C_a d'où [IO₃^-]_é +[HO^-]_é =C_a soit [HIO₃]_é =[HO^-]_é =K_e / [ H₃O⁺]_é

Or K_a = [IO₃^-][H₃O⁺] / [HIO₃] ;K_a =C_a[ H₃O⁺]²_é/K_e ; [ H₃O⁺]²_é=K_aK_e/ C_a = 6,3 10^-2*10^-14/0,5 = 1,26 10^-15

[ H₃O⁺]_é=3,5 10^-8 ; pH_e = 7,45.

indice d'iode des corps gras

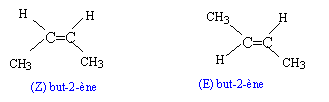
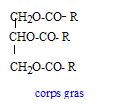
Le diiode de formule chimique I₂ peut donner avec les alcènes des réactions d’addition pour donner un diiodo alcane. La réaction précédemment évoquée est lente, on ajoute donc au milieu réactionnel un catalyseur. C’est ce mode opératoire qui est mis à profit pour déterminer l’indice d’iode des corps gras. Les corps gras sont des triesters du glycérol (ou propanetriol) et d’un acide gras (acide à longue chaîne carbonée pouvant présenter des insaturations).

Donner la formule générale d’un alcène.
En utilisant les caractéristiques de la liaison carbone - carbone pour les hydrocarbures éthyléniques, proposer les isomères possibles des alcènes possédant quatre atomes de carbone ?
Donner la formule chimique du glycérol.
L'acide oléique est un monoacide gras présentant dans sa chaîne carbonée non ramifiée une seule laison de type éthylénique et de formule chimique C₁₈H₃₄ O₂ . Donner sa formule semi-développée sachant que la double liaison se trouve en C₉ C₁₀ .
Donner la formule des corps gras formés entre le glycérol et l’acide oléique que l’on rencontre fréquemment dans de nombreuses huiles (ricin, arachide, olive….).
Quelle réaction chimique peut-on attendre si on fait réagir de l’huile de ricin avec un mélange de diiode et de catalyseur ? Donner la formule semi-développée du composé obtenu.

corrigé

formule générale d’un alcène : C_nH_2n.

but-1-ène CH₂=CH-CH₂-CH₃; 2-méthylpropène CH₂=C(CH₃)₂

formule chimique du glycérol : HOH₂C-CHOH-CH₂OH

formule semi-développée acide oléique : CH₃-(CH₂)₇-CH=CH-(CH₂)₇-COOH

formule des corps gras formés entre le glycérol et l’acide oléique : l'acide oléique est noté R-COOH

réaction chimique attendue si on fait réagir de l’huile de ricin avec un mélange de diiode et de catalyseur :

addition de 3 moles de diiode ( par mole de corps gras) sur les trois doubles liaisons carbone carbone des trois chaînes carbonnées R

R devient alors : CH₃-(CH₂)₇-CH I-CH I-(CH₂)₇-

Préparation acétate de butyle

Protocole expérimental :

Dans un bicol de 250 mL surmonté d’un réfrigérant à reflux et d’une ampoule de coulée et muni d’un système d’agitation magnétique, introduire 50 mL de butan-1-ol. Après l'introduction du butan-1-ol, introduire dans l'ampoule de coulée 30 mL d’acide acétique pur cristallisable et 15 gouttes d’acide sulfurique concentré. En agitant, couler lentement le mélange d’acides.

Chauffer 1 heure à reflux tout en agitant. Refroidir à température ambiante puis couler le mélange réactionnel sur 100 mL d’eau glacée.

Après lavages de la phase organique, séchage et distillation, on obtient l’acétate de butyle purifié.

Questions :

Écrire l’équation chimique de la réaction.
Déterminer les quantités (en moles) de réactifs mis en jeu et calculer le volume théorique d’acétate de butyle que l’on peut obtenir.
Sachant que le rendement de la synthèse est de 70 %, calculer le volume d’acétate de butyle obtenu.
Pourquoi chauffe-t-on le milieu réactionnel ?
Quel est le rôle de l’acide sulfurique et indiquer les caractéristiques de son mode de fonctionnement.

Données

produit	acide éthanoïque ( acétique)	butan-1-ol	acétate de butyle
M(g/mol)	60,05	74,12	116,16
densité	1,0490	0,8098	0,8748
point de fusion °C	16,6	-89,8	-98,9
point ébullition °C	117,9	117,7	112

corrigé

équation chimique de la réaction : CH₃-COOH + CH₃-CH₂-CH₂-CH₂OH = CH₃-COO-CH₂-CH₂-CH₂-CH₃+H₂O

quantités (en moles) de réactifs mis en jeu :

butan-1-ol : masse (g) = volume (mL) * densité = 50*0,8098 = 40,49 g

n(mol) = m(g) / M(butanol) (g/mol) = 40,49 / 74,12 = 0,546 mol.

acide acétique ( même type de calcul ) : 30 *1,049 / 60,05 = 0,524 mol ( en défaut)

On peut obtenir au mieux 0,524 mol d'ester soit une masse égale à 0,524*116,16 = 60,87 g

soit un volume de : 60,87/ 0,8748 = 69,6 mL.

volume d’acétate de butyle obtenu : volume théorique * rendement = 69,6 * 0,7 = 48,7 mL

On chauffe le milieu réactionnel afin d'accélérer la réaction sans changer la composition du mélange à l'équilibre.

l’acide sulfurique catalyse à la fois la réaction d'estérification et la réaction inverse, l'hydrolyse de l'ester : l'équilibre est atteint plus rapidement mais sa composition n'est pas modifiée.

retour -menu