|
d'après
concours Fesic (
physique) 2006
|
|
|
|
|
répondre
vrai ou faux. Ondes
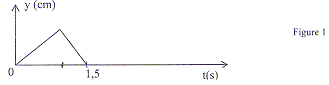
- Une perturbation transversale, d'amplitude y, est
crée en un point S d'une corde dont la direction est initialement
confonfue avec l'axe Sx. L'allure simplifiée de la perturbation au
point S donnée en fonction du temps est donnée figure 1.
A la date t=0 le front de la perturbation quitte l'extrémité S de la
corde. A la date t on prend une photographie instantanée de la corde.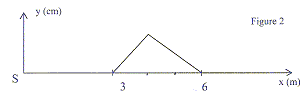
a) L'énergie cinétique est une des formes d'énergie transportées par
l'onde. vrai
b) La célérité de l'onde vaut 2 m/s. vrai T= 1,5 s (
d'après fig 1) ; l=
3 m ( d'après fig 2) ; v= l/T
= 3/1,5 = 2 m/s.
c) L'allure de la corde, figure 2, est photographiée à t = 3 s. vrai
d) si on augmente la tension de la corde, la
célérité de l'onde sera augmentée. vrai
- On émet à l'aide
d'un haut-parleur un signal sonore sinusoïdal. L'onde se propage à la
célérité c= 340 m/s, sa fréquence est f= 425 Hz et on note l sa longueur d'onde.
Données : 340/425 = 0,80 ; 425/340 = 1,25 ; 340*425= 1,45 105.
a) l, f et c sont liés par la relation : l = f/c. faux
c = l f.
b) La longueur d'onde est indépendante du milieu de propagation faux
c) Deux points situés à d= 40,0 cm l'un de l'autre dans la direction de
propagation sont en phase. faux
l = c/f = 340/425 = 0,80 m = 80 cm.
Les deux points n'étant pas distants d'un nombre entier de longueur
d'onde, ne sont pas en phase.
d) L'onde se réfléchit sur un obstacle situé à d'= 34,0 m de la source.
L'écho de l'onde est entendu 1,0 s après l'émission du signal. faux
on suppose que le récepteur se trouve au niveau de
l'émetteur ; l'onde parcourt 34+34 = 68 m avant que l'onde réfléchie ne
soit perçue soit 68/340 = 0,2 s après l'émission.
|
|
radioactivité
- On considère la réaction suivante : AZX+11H--->32He.
|
noyau
|
11H
|
21H
|
31H
|
42He
|
|
nom
|
hydrogène
|
deutérium
|
tritium
|
hélium
|
a) La réaction considérée est une réaction de fusion
thermonucléaire. vrai.
b) AZX est un noyau de
deutérium. vrai. conservation
de la charge Z+1 = 2 soit Z=1 et conservation du nombre de nucléons :
A+1=3 soit A=2.
c) La masse du noyau après réaction est inférieure à la somme des
masses des noyaux avant réaction. vrai.
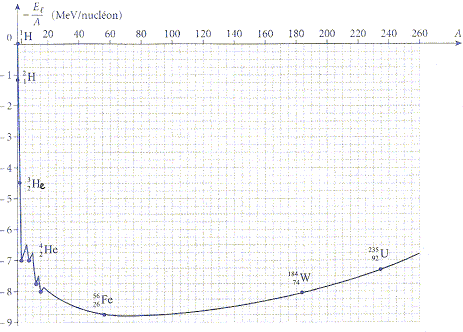
d) D'après la courbe d'Aston, l'énergie libérée par la réaction
considérée est d'environ 4,4 MeV. faux.
4,5*3 - 1,1*2 = 11,3 MeV.
- Le thorium 23090Th
subit une série de désintégrations a
et b-
conduisant à la formation du plomb 20682Pb
stable. La constante de cette désintégration radioactive est l= 8,7 10-6
an-1.
Données : ln2 = 0,7 ; 1/8,7 10-6 =11,5 104
;0,7/8,7 10-6 =8,0 104 ;
ln4 //8,7 10-6 =16 104 .
a) L'équation globale de la désintégration subie par le thorium est : 23090Th---->20682Pb
+ 6a +2 b-
23090Th---->20682Pb
+ 6 42He
+20-1e
; conservation de la charge : 90 = 82+12-2 ( non vérifiée)
faux.
b) La demi vie du thorium 23090Th
est t½= 11,5 104 ans. faux. l
t½ =
ln 2 soit t½ = ln2/l =
ln2 /8,7 10-6 =8,0 104 ans.
c) La quantité de thorium 23090Th
désintégré au cours d'une durée t est proportionnelle à cette durée t. faux. voir la loi de
décroissance radioactive.
d) Un échantillon contient 0,25 mmol de 23090Th
et 0,75 mmol de 20682Pb.
L'échantillon est agé de 2,4 105 ans. faux
Au bout d'une période t½ la
proportion est 0,5 mmol de 23090Th
et 0,5 mmol de 20682Pb.
Au bout de deux périodes 2t½ la proportion est
0,25 mmol de 23090Th et
0,75 mmol de 20682Pb.
or t½ = ln2/l=ln2
/ 8,7 10-6=8 104 ans ; 2 t½
=1,6 105 ans.
- Le nucléide 23994Pu
peut réagir avec un neutron selon la réaction : 23994Pu
+ 10n---->13552Te
+10242Mo +3 10n
Données : masse des nucléide (en MeV/c² )23994Pu
: 222,655 103 ; 10n
: 932 ; 13552Te :
125,662 103 ; 10242Mo
: 94,920 103.
Masse atomique du plutonium 23994Pu
: M= 239 g/mol ; NA= 6 1023
mol-1 ; 1 MeV/c² = 1,6 10-13
J ; 209*1,6 = 330 ; 209/1,6 = 130.
a) Cette réaction est une fusion nucléaire. faux
fission.
b) La perte de masse Dm
est -209 MeV/c². vrai
Dm
=125,662 103 +94,920 103+2*932
-222,655 103 = -209 MeV/c².
c) Cette réaction libère de l'énergie. vrai
d) L'énergie
libérée par la réaction de 239 g de 23994Pu
est E= 2 1013 J. vrai
énergie libérée par une fission : 209*1,6 10-13
J ; énergie libérée par une mole de plutonium : 209*1,6 10-13
* 6 1023 =330*6 1010 =2 1013
J.
|
|
dipôles
RC, RLC
- On branche un condensateur de capacité C, chargé
initialement avec une charge QB= 10-6
C sur l'armature B, aux bornes d'une bobine d'inductance L et de
résistance r non nulle. A t=0 on ferme l'interrupteur K et on
enregistre l'évolution au cours du temps de la tension uAB aux bornes
du condensateur. p² =
10. L'enregistrement est l'une des courbes ci-dessous.
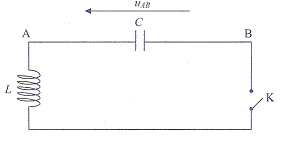
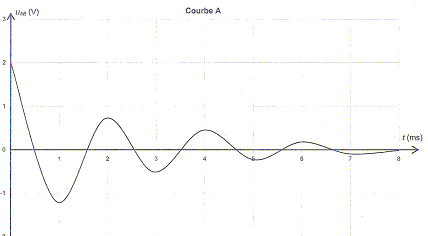
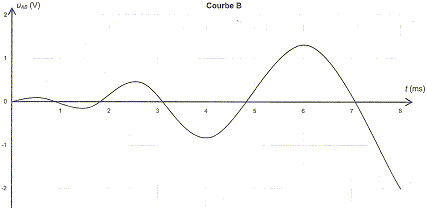
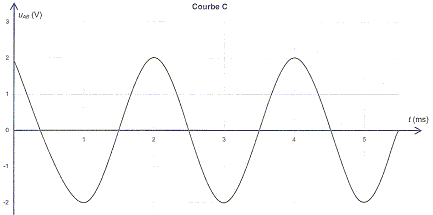
a) La courbe représentant uAB=f(t)
est la courbe A. vrai
b) Le régime transitoire est apériodique. Faux.
pseudo-périodique.
c) La capacité du condensateur est C= 5 10-7 F.vrai
valeur maximale de uAB= 2 V
( graphe A) ; de plus QB= C uAB max
soit C= QB/ uAB max = 10-6
/ 2 = 5 10-7 F.
d) L'inductance de la bobine est L= 0,2 H.vrai
période T² = 4p²
LC soit L= T² /( 4p²
C) avec T= 2 10-3 s ( graphe 2) ; L= 4 10-6
/ ( 4*10*5 10-7) = 0,2 H.
- Le circuit ci-dessous est constitué d'une source de
tension E, d'une inductance de valeur L= 0,1 H, d'un conducteur ohmique
de résistance R=100 W ,
d'un condensateur de capacité C= 100 nF et d'un interrupteur K.
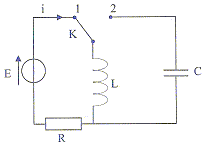
Dans un premier temps, le régime permanent est
établit dans le circuit RL et l'intensité du courant est égale à I= 100
mA.
a) On peut considérer que le régime permanent est établi au bout d'une
durée voisine de 0,10 ms après la fermeture de l'interrupteur en
position 1. Faux.
t=
L/R = 0,1/100 = 10-3 s = 1 ms. le régime
permanent est établit au dela de 5t
= 5 ms.
b) En régime permanent l'énergie stockée dans la bobine vaut 5mJ. Faux.
E= ½LI² = 0,5*0,1*0,1² = 5 10-4
J.
Dans un deuxième temps, le condensateur étant déchargé, on bascule
l'interrupteur en position 2. Il s'établit dans le circuit LC un régime
sinusoïdal.
c) à t=0+, juste après la fermeture de K, la
tension aux bornes du condensateur est nulle. Faux.
d) La valeur maximale de la tension aux bornes du condensateur est
égale à 10 V. Faux
énergie maximale stockée par le condensateur : ½CU²max
= 5 10-4 avec C= 10-7 F ;
U²max =5 10-4 / ( 0,5 10-7)
= 104 ; Umax = 100 V.
- On place en série un générateur de tension de force
électromotrice E constante, un condensateur de capacité C, un
conducteur ohmique R et un interrupteur K.
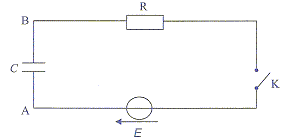
A l'instant t=0 on ferme l'interrupteur K et on
mesure la tension uAB aux bornes du
condensateur. Un logiciel a permis de tracer l'évolution de cette
tension en fonction du temps. R= 104
W.
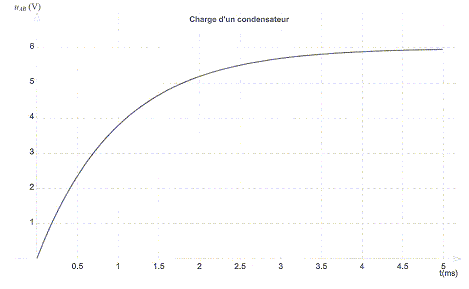
a) la fem E du générateur vaut 6 V. vrai. E= tension aux
bornes du condensateur au bout d'un temps assez long.
b) L'équation différentielle vérifiée par uAB
est uAB+ RC duAB/dt = 0. faux.
uAB+Ri = E avec i = dq/dt et
q=CuAB soit i = CduAB/dt
; uAB+ RC duAB/dt = E.
c) La constante de temps RC du circuit est voisine de t =1 ms. vrai. Sur le graphe
lire l'abscisse correspondante à uAB= 6*0,67 = 4
V.
d) La capacité du condensateur est voisine de C= 1,0 mF. faux
RC= 10-3 s soit C= 10-3/R
= 10-3/104 = 10-7
F = 0,1 m F.
-
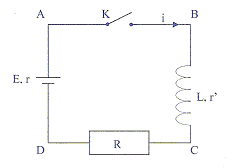
A l'instant t=0 on ferme l'interrupteur K.
L'intensité s'établit progressivement. En régime permanent l'intensité
vaut I= 50 mA. A t=0 la bobine n'a pas emmagasinée d'énergie. E= 5,0 V
; r= 10 W ; r'= 20 W ; L= 0,1 H.
a) à t=0+, juste après la fermeture de
l'interrupteur , i=0. vrai.
b) à t=0+ la tension aux bornes de la bobine est
égale à 0 V. faux ; la
tension aux bornes du résistor R est nulle car i=0 ; la tension aux
bornes de la bobine vaut donc E.
c) R= 70 W. vrai en régime
permanent la bobine se comporte comme un conducteur ohmique : E=
(R+r+r')I soit R= E/I-r-r' = 5/0,05-30 = 70 W.
d) La constante de temps du circuit vaut 1 ms. vrai
L/S
résistances = 0,1 / 100 = 10-3
s.
- L'étude d'un circuit RLC série est effectué avec un
oscilloscope à numérique qui permet de suivre l'évolution de la tenion uc
aux bornes d'un condensateur et de l'intensité du courant dans le
circuit. L'interrupteur K est d'abord placé en position 1 : le
condensateur de capacité C = 10-8 F se charge
grâce à la source de tension de fem E=3 V. A l'instant t=0,
l'interrupteur est basculé en position 2 et simultanément on lance
l'acquisition. p²=10
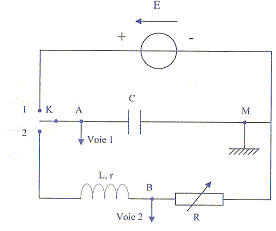
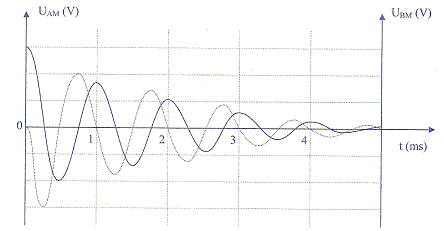
a) On observe des oscillations électriques libres
amorties. vrai.
b) A l'instant t=0+, la tension aux bornes de la
résistance est égale à 3 V. faux.
0 V d'après le graphe en pointillé : tension uBM.
c) L'inductance de la bobine est proche de L= 2,5 H. vrai. T= 10-3
s ; T² = 10-6 = 4p²LC
; L= 10-6/(4p²C)
=10-6/(4*10*10-8) = 2,5 H.
d) Au bout de 2 pseudo-périodes, le circuit a dissipé 8/9 de son
énergie électrique initiale. vrai .
Uc=0, le condensateur ne
stocke pas d'énergie ; la bobine stocke toute l'énergie du dipôle ;
l'intensité du courant vaut 1/3 de la valeur maximale ( à t = 0,25 ms)
; or l'énergie stockée par la bobine est proportionnelle à I² ; I² ne
vaut plus que 1/9 de la valeur maximale ( à t = 0,25 ms).
|
|
Mécanique
- Un mobile autoporteur M, de masse m= 800 , glisse
sans frottement sur un plan incliné faisant un angle a= 10° avec l'horizontale. L'axe
Ox est orienté dans la direction du déplacement. g = 10 m/s² ; sin 10 =
0,17 ; cos 10 = 0,98 ; 8*0,98=7,8 ; 8*0,17 = 1,4.
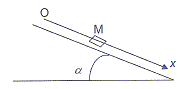
a) Comme il n'y a pas de frottements, la valeur de
la réaction du plan incliné est nulle. faux.
b) la réaction du plan incliné est égale au poids du mobile. faux. mg cosa.
c) Le mobile étant soumis à des forces constantes, son mouvement est
rectiligne uniforme. faux.
La somme vectorielle des forces n'est pas nulle.
d) L'accélération du centre d'inertie du mobile est a = d²x/dt² = 1,4
m/s². faux La
seconde loi de Newton s'écrit sur Ox : ma = mg sin a
soit a = g sina
= 10 * sin 10 = 1,7 m/s².
- Une balle de masse m= 100 g considérée comme un objet
ponctuel est lancée verticalement vers le haut, avec une vitesse
initiale v0 = 12 m/s. Le point de lancement est
pris comme origine d'un axe vertical orienté vers le haut. Au cours de
son mouvement la balle subit des forces de frottements que l'on
admettra proportionnelles à la vitesse, mais de sens contraire, de
valeur f=kv avec k=0,1 SI. g= 10 m/s².
a) Si les frottements étaient négligeables l'altitude maximale atteinte
par la balle serait environ 7,2 m. vrai.
½mv0² = mgh soit h = v0²/(2g)
= 144/20 = 7,2 m.
b) Le coefficient de frottement s'exprime en kg s-1.
vrai. k
= f/v ; f en N soit en kg m s-2 ; v en m s-1
.
c) Lorsque la balle atteint son altitude maximale, son vecteur
accélération est égal au vecteur g. vrai.
la vitesse étant nulle à cette altitude, les
frottements sont nuls ; la balle n'est alors soumise qu'à son poids ;
ma = mg soit a=g.
d) Lorsque la balle retombe elle atteint une vitesse limite vlim
= 10 m/s. vrai. Lorsque
la vitesse limite est atteinte, le poids compense les frottements : mg
= kvlim ; vlim =mg/k =
0,1*10 /0,1 = 10 m/s.
- Lors d'une mission humaine au Darfour ( Soudan), un
avion des Nations Unies, volant horizontalement à l'altitude z= 3000 m,
à vitesse v0 constante, largue en un point S, un
colis de vivres. La résistance de l'air est considérée comme
négligeable devant les autre forces s'exerçant sur le colis. g = 10
m/s² ; 6½=2,4 ; 3½=1,7.
a) Dans le référentiel terrestre la vitesse initiale du colis est v0.
vrai.
b) La trajectoire du colis est un arc de parabole, de sommet S, et
d'axe vertical. vrai.
c) Quand le colis touche le sol, son vecteur vitesse est vertical. faux . La vitesse
possède durant la chute une composante horizontale, non nulle, égale à v0.
d) Le colis touche le sol au bout d'une durée égale à t=24 s. vrai. Sur un axe
vertical orienté vers le bas, d'origine S : z= ½gt² ; au sol z = 3000
soit t² = 2z/g = 600 ; t = 2,4*10 = 24 s.
- Dans un référentiel adapté, Jupiter décrit une
trajectoire quasi-circulaire autour du soleil.
Rayons (km) des orbites: Terre : 1,5 108 ;
Jupiter : 7,8 108. Période orbitale de la Terre
: TT= 8,8 103 h.
1,53 =3,4 ; 7,83 = 470 ;
470/3,4 = 140 ; 7,8/1,5 = 5,2 ; 140½=12 ; 5,2½=2,3.
2p*7,8 = 50 ; 8,8*12 =
100 ; 8,8*2,3 = 20.
a) Le référentiel d'étde le mieux adapté pour cette étude est le
référentiel géocentrique. faux
. héliocentrique.
b) L'accélération de Jupiter est radiale. vrai
. Dirigée vers le centre du soleil si on
néglige les attractions des astres autre que le soleil.
c) Jupiter, trop loin de la Terre, n'est pas soumis à la seconde loi de
Kepler. faux
d) Le
mouvement de Jupiter autour du soleil est un mouvement uniforme et la
valeur de la vitesse de Jupiter est v= 5,0 104
km/h. vrai
3ème loi de Kepler : T²J=T²T(RJ/RT)3
= T²T (7,8/1,5)3 = 140 T²T
: TJ= 12 TT 12*8,8 103
= 105 h.
vJ= 2pRJ/TJ=
2p7,8 108 / 105 =
50 103 km/k
- Un pendule simple constitué d'une masse ponctuelle m=
15 g, placée à l'extrémité d'un fil sans masse, oscille avec une
période T dans un plan vertical.
g= 10 m/s² ; 2p = 6 ; 15½=3,9
; 0,1½= 0,3 ; 10½=3 ; 15-½=0,26.
a) La période T est proportionnelle à la longueur du fil. faux proportionnelle
à la racine carrée de la longueur du fil.
b) Si on double la valeur de la masse, la période T double. faux La
période est indépendante de la masse.
c) La période dépend de l'amplitude si celle-ci est supérieure à 20 °
environ. vrai
d) Pour un pendule de longueur L= 1,0 m, la période vaut T= 0,26 s. faux
T= 2p(L/g)½
=6(1/10)½=6/3 = 2 s.
|
|
photon
- Une radiation de longueur d'onde l=112 nm est émise dans le vide
par un atome d'hydrogène excité.
célérité du son dans l'air : 340 m/s ; célérité de la lumière dans le
vide : 3,0 108 m/s. Constante de plank h= 6,62 10-34
Js.
340/112=3,04 ; 300/112 = 2,68 ; 3,04*6,62 = 20 ; 2,68*6,62 = 17,7.
a) Cette radiation se situe dans l'infrarouge. faux.
dans l'UV.
b) La fréquence de cette radiation est f= 2,68 1015
Hz.vrai. f= c/l = 3
108 / 112 10-9 = 2,68 1015.
c) L'énergie du photon correspondant est : E= 2 10-42
J. faux. E=
h f = 6,62 10-34*2,68 1015
= 17,7 10-19 J.
d) Le spectre de la lumière émise par un ensemble d'atomes d'hydrogène
excités est un spectre de raies d'absorption. faux.
spectre de raies d'émission.
|
|
retour
-menu
|