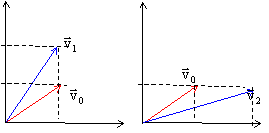|
|
||||
|
||||
|
réponses vraies soulignées, écrites en rouge.
|
||||
corrigé fusion entre deux noyaux d'hydrogène en un noyau de deutérium : 211H --->21H + AZ X conservation de la charge : 2=1+Z d'où Z=1 ; conservation du nombre de nucléons : 2=2+A d'où A=0 ; 01e : positon. fusion d'un noyau d'hydrogène et d'un noyau de deutérium en un noyau d'hélium 3 : 11H + 21H---> 32He Le noyau d'hélium 3 est dans un état excité : il libère de l'énergie sous forme d'un photon en revenant à l'état fondamental. fusion de deux noyaux d'hélium 3 en un noyau d'hélium 4 : 2 32He--->42He + 2 11H ( protons) perte de masse en u correspondant à cette réaction : 4 11H--->42He + 2 01e+ 2g Dm = m(42He)+2m( 01e) - 4m(11H) =4,0026+2*0,0006-4*1,0073 = -0,0254 u énergie libérée par nucléon lors de cette fusion : 0,0254 *1000 = 25,4 MeV soit par nucléon 25,4/6 voisin de 6 MeV/nucléon. perte de masse subie chaque seconde par le soleil : à une masse de 4,0292 u correspond une perte de masse de 0,0254 u à une masse de 7,2 108 t correspond une perte de masse de : 7,2 108 *0,0254/4,0292 = 7,2 108 /160 = 4,5 106 t.
|
||||
|
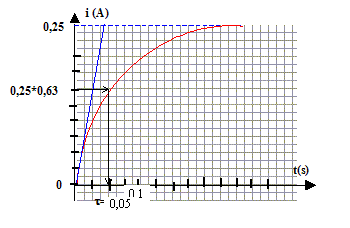
On étudie un circuit série : bobine inductive ( L, r= 12 W), conducteur ohmique R= 12 W, générateur de tension continue E= 6,0 V. 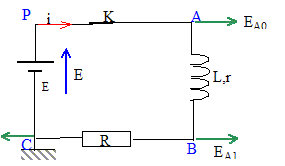 La voie EA0 permet de visualiser E et la voie EA1 permet de visualiser uBC. Le graphe 1 donne l'évolution de l'intensité au cours du temps. 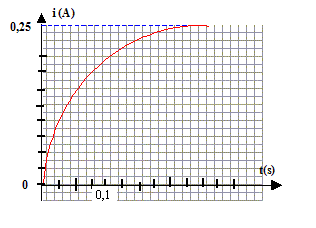
corrigé durée du régime transitoire voisin 0,25 s ( lecture graphe ) expression littérale de t= L/(R+r) soit L= (R+r)t
0,05 = L/(12+12) soit L= 0,05*24 = 1,2 H équation différentielle vérifiée par l'intensité : E = uAB + uBC = Ldi/dt + ri + Ri E= Li' + (R+r) i ; i' + (R+r)/L i = E/L. i(t) = E/(R+r)(1-exp(-t/t)) ; dériver par rapport au temps : i' = E/((R+r)t) exp(-t/t) = E/L exp(-t/t) repport dans l'aquation différentielle : E/L exp(-t/t) + (R+r) /L E/(R+r)(1-exp(-t/t)) = E/L ; E/L exp(-t/t) +E/L - E/L exp(-t/t) = E/L vérifiée quel que soit t donc i(t) = E/(R+r)(1-exp(-t/t)) est solution de l'équation différentielle. expression littérale de I et sa valeur : I= E/(R+r) = 6/24 = 0,25 A, en accord avec le graphe.
|
||||
|
Un golfeur cherche à placer la balle dans le trou du green. On néglige tout mouvement de rotation de la balle sur elle même. OIl fait varier séparément les caractéristiques du vecteur vitesse initiale de la balle. On néglige les frottements de l'air sur la balle. La hauteur maximale H est atteinte pour une abscisse égale à ½D. D= 2v0²cos a sin a/g ; H= v0² sin² a/(2g) 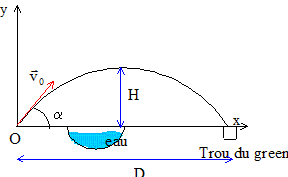
corrigé coordonnées V0x et V0y du vecteur vitesse initiale : V0x =V0 cos a ; V0y =V0 sin a ; Expressions de D et H : D= 2 V0 cos a V0 sin a /g = 2V0xV0y /g. H= V0 sin aV0 sin a / (2g) = V²0y / (2g) Les nouvelles valeurs D1 et H1 : V1x =V0x ; V1y = 2V0y H1 = V²1y / (2g) = 4V²0y / (2g) = 4 H D1 =2V1xV1y /g= 4V0xV0y /g = 2 D ; le coup est loupé. Les nouvelles valeurs D2 et H2 : V2x =2V0x ; V2y = V0y H2 = V²2y / (2g) = V²0y / (2g) = H D2 =2V2xV2y /g= 4V0xV0y /g = 2 D ; le coup est loupé. même angle de tir a mais en frappant plus fort : la valeur de la vitesse croît ; or Het D sont proportionnelles au carré de la vitesse, donc H et D croissent.
|
||||
|
|