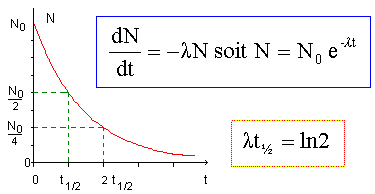|
|
||||||||||||||
|
||||||||||||||
|
La tyroïde est une glande de petite taille, pesant entre 10 g et 30 g, située dans la région cervicale antérieure ; sa fonction principale est la secrétion d'hormones thyroïdiennes synthétisées à partir de l'iode alimentaire. La scintigraphie thyroïdienne est un examen qui permet de mesurer la fixation d'iode par la thyroïde et d'apprécier la fonction thyroïdienne en décelant d'éventuels nodules. L'iode radioactif est le traceur de référence pour cet examen. On utilise souvent l'iode 123, qui se désintègre par capture électronique en émettant un rayonnement g, avec une demi-vie t½ = 13,2 heures. Deux à tris heures
avant l'examen n injcte par voie intraveineuse, une dose d'iode 123 qui
présente une activité A0= 7,0 Mbq (
mégabecquerels). Cet iode radioactif est métabolisé par la thyroïde de
la même façon que l'isotope stable , l'iode 127. L'examen consiste
d'abord à explorer la thyroïde par une caméra à scintillations qui
localise et mesure le rayonnement g
émis par l'iode radioactif : la caméra, associée à un ordinateur,
permet de visualiser l'activité métabolique de la glande.
. corrigé Composition du noyau d'iode 12353I : 53 protons ; 123-53 = 70 neutrons. masse totale que possèdent les nucléons qui participent à la formation du noyau d'iode 123 : 53*1,007825 + 70*1,008665 =53,414725 + 70,60655 = 124,021275 u La masse du noyau
d'iode 123 est inférieure à la somme des masses de ces nucléons séparés
et au repos.
Equation de la réaction nucléaire : 12252Te+ 21H---> 12353I + AZX conservation de la charge : 52+1 = 53+Z d'où Z=0 conservation du
nombre de nucléons : 122+2=123+A d'où A= 1 ; on identifie AZX
à 01n (neutron)
Relation entre la constante radioactive l et la demi-vie t½ : l t½ = ln 2. Expression de l'activité A de l'échantillon à une date t quelconque en fonction des paramètres A0 et t½ : A= A0 exp(-lt) ; l = ln2/t½ ; exp(-lt) = exp(-ln2 t /t½ ) A/ A0 =exp(-ln2 t /t½ ) ; ln(A/ A0)=ln2 (-t /t½ ) = ln(2(-t /t½ )) A= A0 2(-t /t½ ) Activité à t =2 t½ : A= A0 2-2 = A0/4= 7/4 = 1,75 MBq. Courbe donnant les variations de l'activité au cours du temps :A= -dN/dt = l N N(t) et A(t) sont identiques au facteur l près.
|
||||||||||||||
|
Un condensateur de capacité C= 0,20 mF, initialement chargé sous une tension continue constante U0= 6 V est associé à une bobine d'inductance L= 0,5 H. On considère l'instant initial t=0, à l'instant où l'on associe le condensateur à la bobine. 
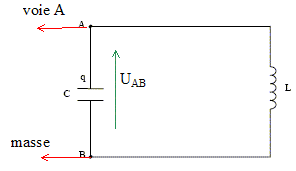
corrigé branchements à effectuer pour visualiser sur la voie A de l’oscilloscope la tension UAB :
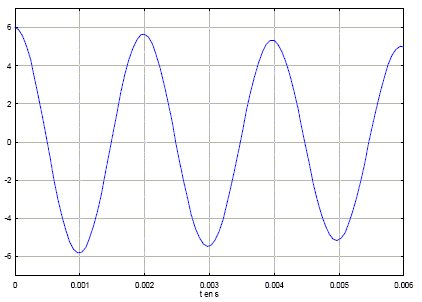
équation différentielle régissant l’évolution temporelle de la charge q du condensateur : additivité des tensions : UAB + UBA=0 UAB =q/C et UBA= L di/dt ; de plus i = dq/dt soit di/dt = d²q/dt² doù : q/C + L d²q/dt² = 0 ; d²q/dt² + 1/(LC) q=0. expression de q(t) en fonction des constantes U0, C et L et du paramètre t : solution générale de l'équation différentielle : q(t) = A exp(-t/(LC)) condition initiale q= CU0= A exp(0) = A d'où : q(t) = CU0 exp(-t/(LC)) Expression de la période propre T0 des oscillations : w02 = 1/(LC) et T0 = 2p/w0 ; T0 = 2p(LC)½ valeur de T0 = 2 p(0,5*0,2 10-6)½ =2 p / 10½ ( 10-6)½ = 2 10-3 s. régime d’oscillations constaté : pseudopériodique ( l'amplitude décroît au cours du temps ) |
||||||||||||||
|
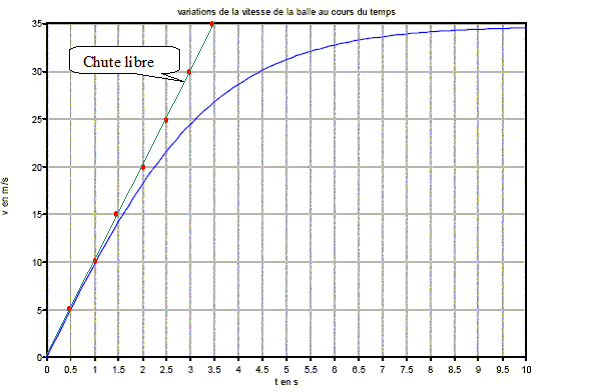
Les balles de golf font l’objet d’études assez poussées. Le modèle américain, le seul utilisé en compétition satisfait aux normes internationales : sa masse est de 45,9 g et son diamètre de 42,7 mm. Masse m = 45,9g ; Diamètre D = 42,7 mm La balle comporte 384 alvéoles qui empêchent l’air de se décoller de la surface lorsque la vitesse de la balle est grande, de ce fait, la balle est « moins freinée » que si elle était parfaitement lisse. Afin de simplifier les calculs, on utilisera dans l’exercice les données numériques suivantes : Masse m = 48 g ; Diamètre D = 40 mm. On étudie la chute verticale dans l’air d’une balle et plus précisément le mouvement de son centre d’inertie. La balle est lâchée sans vitesse initiale en O. La verticale passant par O est orientée par un vecteur unitaire j dirigé vers le bas, donc de même sens que le vecteur champ de pesanteur g. On prendra g = 10 m.s-2. La position de la balle est caractérisée par l’ordonnée y de son centre d’inertie dans le repère (O, j) et sa vitesse instantanée est v= dy/dt Premier modèle : chute libre :
Second modèle : prise en compte de la résistance de l’air : On décide de prendre en compte les actions mécaniques exercées par l’air. La résistance que l’air oppose au mouvement de la balle est supposée agir verticalement, dans le sens opposé à celui du mouvement, avec une valeur proportionnelle au carré de la vitesse : F = k v2.
Comparaison des deux modèles : On pose C=k/m, l’équation différentielle du second modèle s’écrit alors dv/dt =g-Cv². On programme la résolution de cette équation différentielle par la méthode d’Euler, avec une vitesse initiale nulle, un pas de calcul Dt = 0,10 s, des constantes g = 10 m.s-2 et C = 8,33.10-3 s-1. On rappelle l’approximation consentie dans la méthode d’Euler : v(t+Dt) = v(t) + D t a(t) avec a(t) =dv/dt(t)
corrigé Premier modèle : chute libre : Un solide soumis uniquement à son poids est en chute libre. Expression de la vitesse instantanée v en fonction de t et de g : sur un axe vertical descendant, la seconde loi de Newton s'écrit : mg=ma soit a=g. La vitesse est une primitive de l'accélération : v=gt + v0 avec v0 : vitesse initiale. si v0 =0 alors v=gt = 10 t. nature du mouvement : rectiligne uniformément accéléré. Expression de l’ordonnée y en fonction de t et g : l'ordonnée est une primitive de la vitesse : y= ½gt²+v0t + h0 avec h0 : altitude initiale si v0=0 et si h0=0 alors y = ½gt² = 5 t². Distance parcourue à t=3 s :y = 5*3²= 45 m. vitesse atteinte à t=3 s : v=10*3 = 30 m/s.
On décide de prendre en compte les actions mécaniques exercées par l’air. La résistance que l’air oppose au mouvement de la balle est supposée agir verticalement, dans le sens opposé à celui du mouvement, avec une valeur proportionnelle au carré de la vitesse : F = k v2. Poussée d’Archimède exercée par l’air sur la balle : masse volumique de l’air vaut 1,2 kg.m-3 Pa= rair Vg = 1,2*10 V= 12 V ; V= 4/3pR3 = 4/3*3,14*(0,04)3 =2,7 10-4 m3 ; Pa=3,2 10-3 N. poids de la balle P=mg = 48 10-3*10 = 0,48 N La poussée d'Archimède est est bien négligeable devant son poids. Equation différentielle relative à la vitesse : la balle est soumise à son poids, vertical, vers le bas, valeur mg et à la force de frottement verticale, vers le haut, valeur kv². suivant un axe verticale descendant, la seconde loi de Newton s'écrit : mg-kv²= mdv/dt ; dv/dt = g-k/mv² ; dv/dt +k/mv2=g. Ce modèle est bien compatible avec l’existence d’une vitesse limite vlim dont l'expression est : la valeur de la force de frottement augmente avec la vitesse ; lorsque le poids et la force de frottement se neutralisent, le mouvement devient rectiligne uniforme. k/mvlim2=g ; vlim = (mg/k)½. Des essais en soufflerie ont permis d’évaluer la constante k pour la balle de golf et dans les conditions supposées de l’expérience : k = 4.10-4 kg.m-1. Calcul de vlim
=(48 10-3*10 /4.10-4 )½
=(12 *100)½ =34,6
m/s.
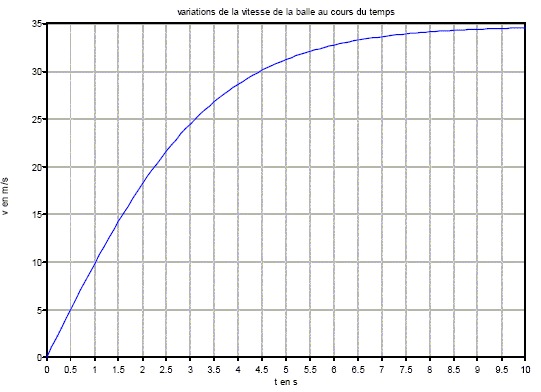
On pose C=k/m, l’équation différentielle du second modèle s’écrit alors dv/dt =g-Cv². On programme la résolution de cette équation différentielle par la méthode d’Euler, avec une vitesse initiale nulle, un pas de calcul Dt = 0,10 s, des constantes g = 10 m.s-2 et C = 8,33.10-3 m-1. On rappelle l’approximation consentie dans la méthode d’Euler : v(t+Dt) = v(t) + D t a(t) avec a(t) =dv/dt(t) A l’aide de la méthode d’Euler, valeurs de la vitesse et de l’accélération à l’instant t1 = 0,10s : à t=0 , a(0)=g=10 m/s² ; v(t=0) = 0 m/s v(0,1) = v(0)+ D t a(0) = 0+0,1*10 = 1m/s. [dv/dt ]0,1=g-Cv² = 10-8,33.10-3 * 1²= 9,99 m/s². Les calculs sont effectués jusqu’à la date t100 = 10 s, on obtient la représentation graphique qui figure sur la feuille jointe.
Le modèle de la chute libre valide pour une durée de chute inférieure à 1,5 s ( les deux courbes sont pratiquement confondues) La vitesse réelle est inférieure à la vitesse trouvée par le modèle de la chute libre : d'où la disposition des deux courbes. temps caractéristique t associé au second modèle : abscisse de l'intersection de la tangente à l'origine de la courbe bleue avec l'asymptote horizontale ( vlim = 34,6 m/s) Le graphe donne environ 3,5 s.
|
||||||||||||||
|
|
||||||||||||||