Aurélie 30/11/06
circuit RLC ; la houle d'après concours EMIA 2004 ( école militaire interarmes)

Google

Circuit RLC : (6 points)

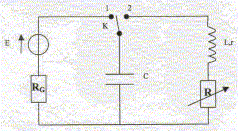
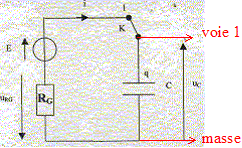
Données : l'alimentation est supposée parfaite ; RG résistance inconnue ; C= 2mF ; L= 5 mH; r= 5 W ; R résistance variable.

Charge du condensateur :

Le condensateur étant déchargé, on bascule à l'instant t=0, l'interrupteur en position 1. On obtient donc le circuit suivant :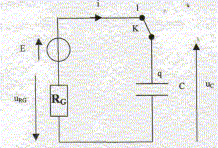

  1. Préciser les branchements à effectuer pour visualiser la tension uC sur la voie 1 de l'oscilloscope à mémoire.
  2. On visualise également la tension uRG sur la voie 2 et on obtient les enregistrements suivants :


    - Quel enregistrement correspond à la tension uC ? Justifier. Même question pour uRG ?
  3. Quelle est la relation entre uRG, E et uC ?
  4. Quelles sont les relations entre i et q et entre q et uc ?
  5. En déduire l'équation différentielle satisfaite par la tension uc(t).
  6. Vérifier que uc(t) = E(1-exp(-t / (RGC))) est solution de cette équation.
  7. Quelle est l'expression littérale de la constante de temps t du circuit ?
  8. Déterminer graphiquement t et en déduire RG.
  9. Déterminer la valeur de E.
  10. Calculer littéralement puis numériquement l'énergie emmagasinée dans le condensateur en fin de charge.

Oscillations libres du circuit RLC :

le condensateur étant supposé complétement chargé, on bascule à t=0 l'interrupteur K sur la position 2. On obtient donc le circuit suivant :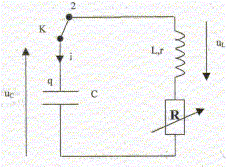

  1. Exprimer uL en fonction de r, L et di/dt.
  2. On suppose tout d'abord que la résistance totale du circuit est négligeable.
    - Etablir l'équation différentielle régissant l'évolution temporelle de la charge q.
    - En déduire l'expression littérale de la période propre T0 des oscillations.
    - Calculer T0 en prenant p=3,14.
  3. En réalisant le montage sans la résistance variable (R=0), on obtient l'oscillogramme suivant :

    - Comment appelle t-on le régime correspondant ?
    - Nommer et définir la durée caractéristique associée à ce régime.
    - Déterminer graphiquement cette durée. Commentaires ?

  4. En modifiant la valeur de R, on peut pbserver deux autres régimes du circuit RLC. Nommer ces régimes.

 

corrigé
Les branchements à effectuer pour visualiser la tension uC sur la voie 1 de l'oscilloscope à mémoire :

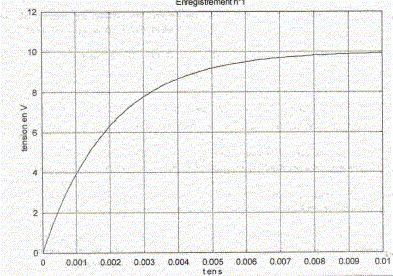
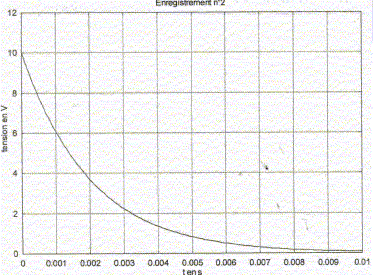
L'enregistrement 1 ( à gauche) correspond à la tension uC : celle-ci est croissante de zéro à E lors de la charge.

L'enregistrement 2 ( à droite) correspond à la tension uRG : l'intensité ( donc uRG qui est égale à RGi) décroît au cours de la charge.

Additivité des tensions : E = uC +uRG.

relations entre i et q : i = dq/dt ; entre q et uc : q=Cuc ; dq/dt = Cduc/dt.

Equation différentielle satisfaite par la tension uc(t) :

E = uC +uRG ; E = uC +RGi ; E = uC +RGCduc/dt. (1)

Vérifions que uc(t) = E(1-exp(-t / (RGC))) est solution de cette équation :

dériver uc(t) par rapport au temps : duc/dt = E/(RGC)exp(-t / (RGC))

repport dans (1) : E(1-exp(-t / (RGC))) + E exp(-t / (RGC)) = E

relation vérifiée quel que soit t : donc uc(t) = E(1-exp(-t / (RGC))) est bien solution de (1).

Expression littérale de la constante de temps t du circuit : t = RGC.

Détermination graphiqu de t :

d'où RG = t/C = 2 10-3 / 2 10-6 = 1000 W.

Energie emmagasinée dans le condensateur en fin de charge :

½CE² = 0,5* 2 10-6 *100 = 10-4 J.

Oscillations libres du circuit RLC :

Le condensateur étant supposé complétement chargé, on bascule à t=0 l'interrupteur K sur la position 2.

Expression de uL en fonction de r, L et di/dt : uL= Ldi/dt + ri

On suppose tout d'abord que la résistance totale du circuit est négligeable.
Equation différentielle régissant l'évolution temporelle de la charge q :

additivité des tensions : uc+uL= 0 ; q= Cuc; i= dq/dt di/dt = d²q/dt²

q/C + Ld²q/dt² = 0 ; q+ LCd²q/dt² = 0 ; q/(LC)+ d²q/dt² = 0

w²0q+d²q/dt² = 0. avec w²0 = 1/(LC)
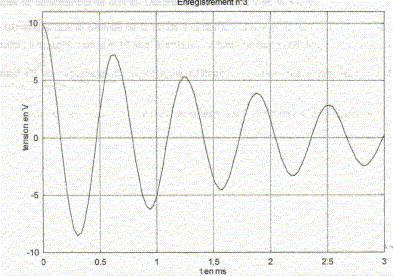
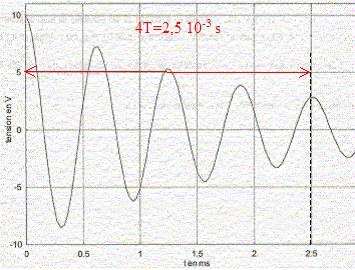
période propre T0 des oscillations :

T0 = 2p/ w0 = 2p(LC)½ = 6,28 (5 10-3*2 10-6)½ = 6,28 10-4 s.

En réalisant le montage sans la résistance variable (R=0), on obtient l'oscillogramme suivant :

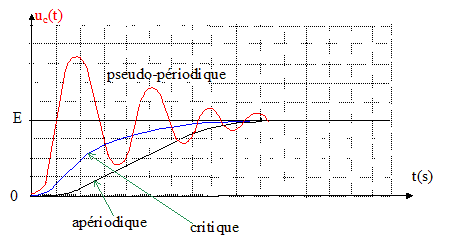
Le régime correspondant est "pseudo-périodique".
Période T associée à ce régime : T = 2,5 10-3/4 =6,25 10-4 s.

T et T0 sont très proches si l'amortissement est faible.

En modifiant la valeur de R, on peut pbserver deux autres régimes du circuit RLC.

La houle : (4 points)

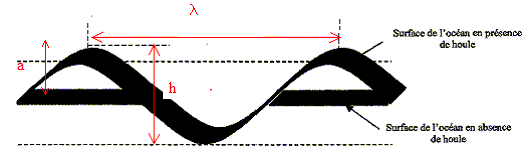
 La houle à la surface de la mer est assimilable à une onde mécanique périodique progressive. Le physicien la caractérise par sa période T, sa longueur d'onde l, sa célérité v et par son amplitude a. Quand un marin parle d'un creux de 9 m, il caractérise la houle par son hauteur crête à crête que l'on notera h.

  1. Représenter l'onde sur la copie en faisant apparaître l, a et h.
  2. Quelle est la relation liant a et h ?
  3. Comment peut-on expérimentalement évaluer la période T ?
  4. Quelle est la nature de l'onde mise en jeu à la surface de l'eau ?
  5. Comment peut-on montrer simplement qu'il y a transport d'énergie mais sans transport de matière ?
  6. Un observateur constate que l'eau vient battre le quai toutes les 10 secondes. En regardant attentivement les bouées de signalisation régulièrement réparties à la surface de l'eau, il remarque que la distance minimale entre deux bouées qui oscillent verticalement en même temps à cause de la houle est de 200 m. Déterminer la célérité de la houle.
  7. En admettant que la célérité de la houle à la surface d'une profondeur H d'eau est donnée par v= (gH)½ où g = 10 m/s², estimer la hauteur moyenne de l'eau dans le cas précédent.
  8. Quand on se rapproche de la côte, la célérité de l'onde augmente t-elle ou diminue t-elle ?
  9. En arrivant sur le rivage, les vagues se brisent ou "déferlent". Expliquer pourquoi il en est ainsi ?
corrigé
La houle à la surface de la mer est assimilable à une onde mécanique périodique progressive. Le physicien la caractérise par sa période T, sa longueur d'onde l, sa célérité v et par son amplitude a. Quand un marin parle d'un creux de 9 m, il caractérise la houle par son hauteur crête à crête que l'on notera h.

Relation liant a et h : a = ½ h.

Evaluer expérimentalement la période T : mesurer la durée séparant deux vaques consécutives venant frapper une digue.

Nature de l'onde mise en jeu à la surface de l'eau : onde mécanique progressive périodique.

Il y a transport d'énergie : les vagues peuvent détruire ou endommager une digue ;

Il n'y a pas transport de matière : un objet situé sur la mer se déplace verticalement.

Un observateur constate que l'eau vient battre le quai toutes les 10 secondes. En regardant attentivement les bouées de signalisation régulièrement réparties à la surface de l'eau, il remarque que la distance minimale entre deux bouées qui oscillent verticalement en même temps à cause de la houle est de 200 m.

l= 200 m ; T= 10 s ; la célérité de la houle est : v = l /T= 20 m/s.

En admettant que la célérité de la houle à la surface d'une profondeur H d'eau est donnée par v= (gH)½ où g = 10 m/s², la hauteur moyenne de l'eau dans le cas précédent est :

H=v²/g = 20*20/10 = 40 m.

Quand on se rapproche de la côte, si la profondeur de l'eau diminue alors la célérité de l'onde diminue ( v est proportionnelle à H½).

En arrivant sur le rivage, les vagues se brisent ou "déferlent" : la profondeur étant faible, le bas de la vague vient heurter le fond de la mer.
retour -menu