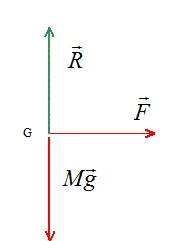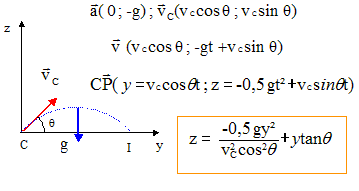Aurélie 10/04/06
Mouvement d'une automobile

d'après concours kiné EFOM 2006

Google

Mouvement d'une automobile( 5 pts).

A- Une automobile de masse M=1,6 t démarre, sans vitesse initiale sur une route rectiligne horizontale. La phase de démarrage est une phase d'accélération pendant laquelle aucune force ne s'oppose à l'avancement, alors que le moteur exerce une force constante , de valeur F, parallèle au déplacement.

  1. Faire le bilan des forces extérieures s'exerçant sur la voiture.
    - En donner une représentation au point G, centre d'inertie de la voiture à un instant quelconque.
  2. L'auto parcourt la distance OA=L=700 m et atteint la vitesse v= 126 km/h. A laide du théorème du centre d'inertie, établir la relation entre F et la valeur a de l'accélération.
    - A l'aide du théorème de l'énergie cinétique, établir la relation entre la valeur F de la force et la vitesse v.
    - En déduire une relation entre vitesse et accélération.
    - Calculer la valeur de l'accélération. et en déduire la valeur de la force F.

B- L'auto aborde en A, avec la vitesse vA= 126 km/h une portion de route rectiligne horizontale AB de longueur l, puis une portion BC circulaire de cente O, de rayon R= 100 m, telle que OC fait avec la verticale un angle q= 60°. Les frottements sont négligeables.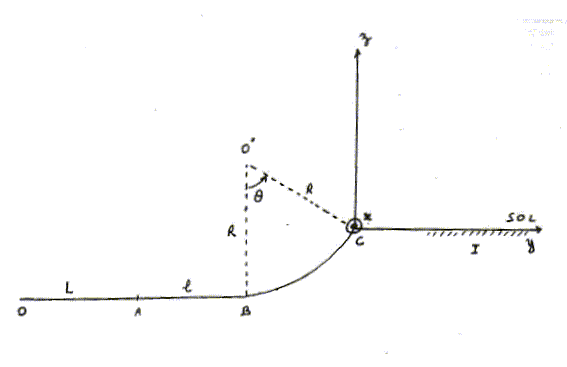

  1. L'automobile arrive en B. Calculer vB.
  2. A l'aide du théorème de l'énergie cinétique appliqué au tronçon BC établir la relation liant vC à vB, R, g et q.

C- Que devient la trajectoire du centre d'inertie G de la voiture après C ?

  1. Déterminer les équations horaires du mouvement dans le repère Cxyz.
  2. En déduire l'expression littérale de l'équation de la trajectoire.
  3. Préciser la nature de cette trajectoire.
  4. Préciser la nature du mouvement sur cette trajectoire.
  5. L'auto retombe sur le sol en un point I. Calculer littéralement l'abscisse de I.

Données : g=10 m/s² ; sin 30 = cos60 = 0,5 ; sin 60 = cos 30 = 0,87.

corrigé
bilan des forces extérieures s'exerçant sur la voiture :

poids, vertical, vers le bas, valeur Mg = 1,6 104 N ; action du support, vertical, vers le haut, opposée au poids, valeur R= 1,6 104 N ; force motrice , parallèle à la route, sens du mouvement, valeur F.

Relation entre F et la valeur a de l'accélération : écrire la seconde loi de Newton sur un axe horizontal, vers la droite : F= Ma

Relation entre la valeur F de la force et la vitesse v : écrire le th. de l'énergie cinétique ( vitesse initiale nulle ; seule F travaille et effectue un travail moteur W= F L)

½Mv² = FL
Relation entre vitesse et accélération : v² = 2aL
valeur de l'accélération : a =v²/(2L) avec v = 126 / 3,6 = 35 m/s et 2L= 1400 m ; a = 35*35/1400 = 0,875 m/s²

valeur de la force F : F= Ma = 1,6 103*0,875 = 1,4 103 N.

Sur le tronçon AB, l'auto est soumise à son poids et à l'action du support : ces deux forces perpendiculaires à la vitesse ne travaillent pas et en conséquence la valeur de la vitesse n'est pas modifiée. vB=vA = 35 m/s.

relation liant vC à vB, R, g et q :

Sur le tronçon BC, l'auto est soumise à son poids et à l'action Rdu support : R perpendiculaire à la vitesse ne travaille pas.

En montée le travail du poids est résistant ; la différence d'altitude entre B et C vaut : R(1-cosq)

d'où le travail du poids : -MgR(1-cosq)

Ecrire le théorème de l'énergie cinétique entre B et C : ½MvC²-½MvB² = -MgR(1-cosq)

vC²-vB² = -2gR(1-cosq) ; vC²=vB² -2gR(1-cosq).

vC² = 35²-20*100*(1-cos60)= 1225-1000 = 225 ; vC= 15 m/s.

La trajectoire du centre d'inertie G de la voiture après C est une branche de parabole : la voiture n'est soumise qu'à son poids ( chute libre avec vitesse initiale non colinéaire au poids)

équations horaires du mouvement dans le repère Cxyz :

abscisse de I : zI=0 d'où y=0 ( correspond au point C)

et 0,5 g y/ ( vC² cos²q) = sin q / cosq ; y I= 2vC² sin q cosq / g = vC² sin (2q) / g

y I=35² sin120 / 10 = 106 m.
retour -menu