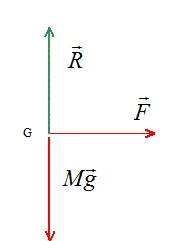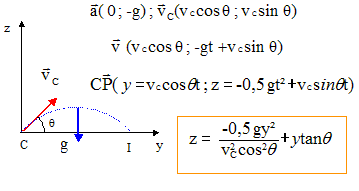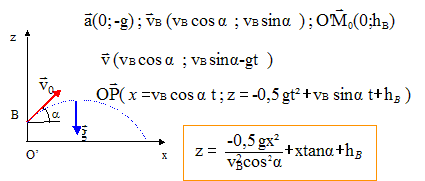|
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
A- Une automobile de masse M=1,6 t démarre, sans vitesse initiale sur une route rectiligne horizontale. La phase de démarrage est une phase d'accélération pendant laquelle aucune force ne s'oppose à l'avancement, alors que le moteur exerce une force constante , de valeur F, parallèle au déplacement.
B- L'auto aborde en A, avec la vitesse vA= 126 km/h une portion de route rectiligne horizontale AB de longueur l, puis une portion BC circulaire de cente O, de rayon R= 100 m, telle que OC fait avec la verticale un angle q= 60°. Les frottements sont négligeables. 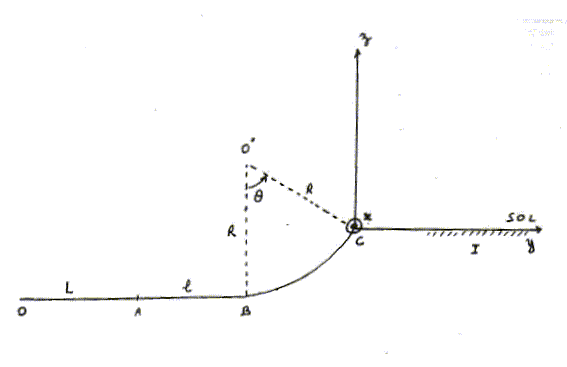
C- Que devient la trajectoire du centre d'inertie G de la voiture après C ?
Données : g=10 m/s² ; sin 30 = cos60 = 0,5 ; sin 60 = cos 30 = 0,87. corrigé bilan des forces extérieures s'exerçant sur la voiture : poids, vertical, vers le bas, valeur Mg = 1,6 104 N ; action du support, vertical, vers le haut, opposée au poids, valeur R= 1,6 104 N ; force motrice , parallèle à la route, sens du mouvement, valeur F.
Relation entre F et la valeur a de l'accélération : écrire la seconde loi de Newton sur un axe horizontal, vers la droite : F= Ma Relation entre la valeur F de la force et la vitesse v : écrire le th. de l'énergie cinétique ( vitesse initiale nulle ; seule F travaille et effectue un travail moteur W= F L) ½Mv² = FL valeur de la force F : F= Ma = 1,6 103*0,875
= 1,4 103 N.
relation liant vC à vB, R, g et q : Sur le tronçon BC, l'auto est soumise à son poids et à l'action Rdu support : R perpendiculaire à la vitesse ne travaille pas. En montée le travail du poids est résistant ; la différence d'altitude entre B et C vaut : R(1-cosq) d'où le travail du poids : -MgR(1-cosq) Ecrire le théorème de l'énergie cinétique entre B et C : ½MvC²-½MvB² = -MgR(1-cosq) vC²-vB² = -2gR(1-cosq) ; vC²=vB² -2gR(1-cosq). vC²
= 35²-20*100*(1-cos60)= 1225-1000 = 225 ; vC= 15 m/s.
équations horaires du mouvement dans le repère Cxyz :
abscisse de I : zI=0 d'où y=0 ( correspond au point C) et 0,5 g y/ ( vC² cos²q) = sin q / cosq ; y I= 2vC² sin q cosq / g = vC² sin (2q) / g y I=35² sin120 / 10 = 106 m.
|
|||||||||||||||||||||||||
|
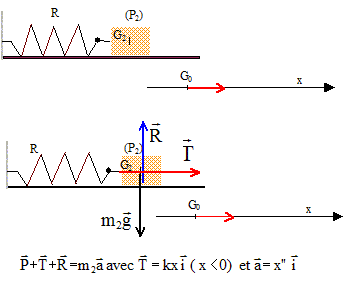
Un palet P1 de masse m1 est propulsé le long d'une piste à coussin d'air. La piste comporte une rampe AB de longueur L inclinée d'un angle a sur l'hotizontale, suivie d'un trou T afin de recevoir ce palet. Le palet P1 est propulsé grâce à un choc avec un palet P2, de masse m2 = 4 m1. Le palet P2 est lui même relié à un ressort R horizontal, de masse négligeable et de constante de raideur k. L'autre extrémité du ressort est fixe en O. A l'équilibre, la position du centre d'inertie du palet P2 est notée G0 telle que OG0 = l0. Tous les frottements sont négligés ; Lors du choc le palet P2 transmet intégralement son énergie cinétique au palet P1 ; le ressort exerce une force proportionnelle à sa déformation. 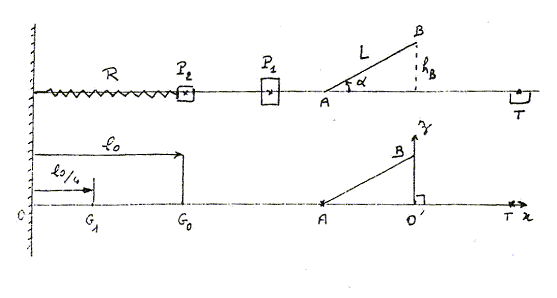 Etude du mouvement du palet P2 : Un joueur comprime le ressort : la nouvelle position du centre d'inertie G2 du palet devient G1 telle que OG1 = 0,25 l0. Puis ce même joueur le lâche à un instant pris comme origine des dates, sans communiquer de vitesse initiale à P2.
Etude du mouvement du palet P1 : le choc entre les palets a lieu lorsque le centre d'inertie G2 du palet P2 passe en G0.
m1 = 50 g ; m2 = 200 g ; k = 20 N/m ; l0 = 24 cm ; g= 10 m/s² ; a= 30°. aide au calcul : p²=10 ; sin 30 = 0,5 ; cos 30 = 0,87 ; tan30 = 0,58 ; 3,6²= 13 ; 1,4²=2 ; 18²= 324 ; 8*0,87 = 7 corrigé équation différentielle du mouvement du centre d'inertie du palet P2 :
soit en projection sur G0x : -kx=m2x" ou bien x" + k/m2 x=0 nature du mouvement de G2 : le mouvement ne dure que 1/4 de période , donc rectiligne non uniformement accéléré. signification physique de A ( amplitude), w0(
pulsation) f ( phase à
t=0) à t=0 x(0) = -0,75 l0 = A cosf avec A positif donc f = p
et A = 0,75 l0 . v(t) = -Aw0
sin (w0t+p) énergie mécanique du système ressort et palet à un
instant t quelconque : ½kx²+½m2v²= ½kA² conservation de l'énergie mécanique : ½m2v0²
=½kA² ; v0² = kA² /m2 ; v0
= A(k/m2)½ =1,8 m/s.
conservation de l'énergie cinétique :½m2v0² = ½m1v1² ; v1² = m2v0² /m1 = 4 v0² soit v1 = 2v0 = 3,6 m/s vitesse vA du centre d'inertie G1 du palet P1 au passage en A : aucune force ne travaille entre G0 et A donc vA= v1. La vitesse v2 = 3,6 m/s prévue est en accord avec les hypothèses formulées au départ. vitesse vB au passage au sommet de la rampe : sur la rampe, l'action du plan, perpendiculaire à la vitesse, ne travaille pas ; le travail du poids est résistant en montée et dépend de la différence d'altitude hB = L sin a. ( W= -m1ghB) Ecrire le théorème de l'énergie cinétique entre A et B : ½m1vB² - ½m1vA² = -m1ghB soit : vB² =vA² -2ghB = 3,6²-20*0,25 = 13-5=8 ; vB= 2,8 m/s. longueur L de la rampe : hB= L sin a soit L =0,25 / 0,5 = 0,50 m. équation de la trajectoire du centre d'inertie G1 du palet P1au delà de B, dans le repère O'xz :
z = -0,825 x² +0,58 x+0,25 expression littérale, puis numérique, de la vitesse du palet P1 retombant sur le sol : sur le parcours A I (impact au sol), écrire le théorème de l'énergie cinétique sachant que le poids ne travaille pas ( A et I ont la même altitude) et que l'action du plan est perpendiculaire à la vitesse : aucune force ne travaille et en conséquence la valeur de la vitesse au sol est égale à vA. ou bien : v²= [vBcos a)2+ (vBsins a-gt)2]½. Il faut déterminer t en écrivant qu'au sol z =0 soit 0 = -5t² + 2,8 t +0,25 distance du point O' au trou : écrire qu'au sol z=0 soit -0,825 x² +0,58 x+0,25=0 solution positive à retenir x =1 m. |
|||||||||||||||||||||||||
|
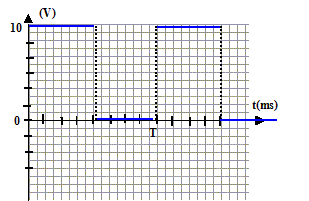
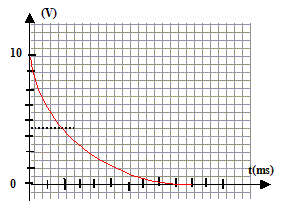
On associe en série un générateur basse fréquence (GBF), un résistor (R= 10 kW) , un condensateur de capacité C= 10mF et un interrupteur. Le GBF délivre une tension u, rectangulaire telle que : u(t)=U0 =10 V sur l'intervalle [0 ; ½T] et u(t) = 0 sur l'intervalle [½T, T]
corrigé
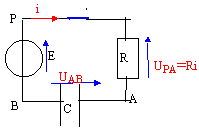
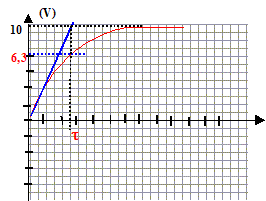
uPB= U0 ; uPB= uPA+ uAB avec i = dqA/dt = CduAB/dt . U0 = Ri +uAB soit U0 =RC duC/dt +uC (1) uc= A(1-exp(-at)) dériver l'expression de uC par rapport au temps : duC/dt = Aa exp(-at). repport dans (1) : U0 = RCAa exp(-at)+A(1-exp(-at)) U0 = A(RCa -1)exp(-at) +A égalité vérifiée quel que soit le temps, en conséquence A= U0 et a =1/(RC) = 1/(104*10-5) = 10 s A : amplitude de la tenion uC (V) ; a =1/(RC) inverse de la constante de temps ( seconde-1 ) du dipôle RC. uC(t) = U0(1-exp(-t/(RC)))= 10 ( 1-exp(-10t)) la solution trouvée satisfait aux conditions initiales en effet : uC(0) = 10(1-exp(0)) = 0 ( condensateur non chagé) allure de la courbe uc(t)
dans le cas ou ½T est très supérieur au produit RC. énergie stockée à chaque instant par le condensateur :
½CuC². ln(10-3) = -10 t1
; t1 = -0,1 ln(10-3) =0,69 s.
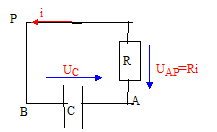
uC(t') = Ri avec i = -dq/dt et q= CuC soit i = -CduC/dt uC(t')+RCduC/dt =0 (1) solution de l'équation différentielle : uc= Bexp(-bt). Valeurs de B et b : dériver l'expression de uC par rapport au temps : duC/dt = -Bb exp(-bt). repport dans (1) : B exp(-bt)
-Bb RC exp(-bt) =0 égalité vérifiée quel que
soit le temps, en conséquence b =1/(RC)
= 1/(104*10-5) = 10 s à l'instant t'=0 uc(0) = U0
= 10 V d'où B = 10 V et uc= 10 exp(-10t). La solution trouvée
satisfait aux conditions initiales énergie stockée à chaque instant par le condensateur :
½CuC². uC(t'2) = 0,37 *10 = 10 exp(-10t'2) ; 0,37 = exp(-10t'2) ; -10t'2 = ln 0,37 = -1 soit t'2 = 0,1 s.
|
|||||||||||||||||||||||||
|
A- Définir un acide fort au sens de Brönsted
B- On dispose d'une solution S1
d'un monoacide A1H de concentration c1
et de pH1= 2,4. A partir de S1
on prépare une solution aqueuse S'1 de
concentration c'1 = c1/10.
Le pH de S'1 a pour valeur 2,9. En déduire si A1H
est un acide fort ou faible. Justifier. C- Définir la constante d'acidité d'un couple acido
basique AH/A-. D- A un volume v1 = 50 mL de solution S1, on ajoute un volume d'une solution aqueuse S2 d'hydroxyde de sodium de concentration c2 = 0,10 mol/L. Quel volume v2 de la solution S2 faut-il ajouter pour obtenir l'équivalence acido basique. Justifier la valeur du pH à l'équivalence. - Quel volume v'2 de la solution S2 faut-il ajouter pour obtenir un mélange de pH=3,8 ? Comment s'appelle une telle solution ? corrigé un acide fort au sens de Brönsted : espèce susceptible de céder un proton ; la réaction avec l'eau est totale. Le pH d'une solution aqueuse S d'un monoacide fort AH
est égal à 2,7. Sa concentration est telle que pH=-log C soit C= 10-pH
= 10-2,7 = 2,0 10-3 mol/L.
équation de la réaction entre A1H
et l'eau : A1H + H2O = A1-
+ H3O+.
la constante associée à l'équilibre ci-dessus est la constante d'acidité Ka du couple AH/A- : Ka = [A-][H3O+] / [AH] constante d'acidité Ka du couple A1H/A1- : [A1-]=[H3O+] = 10-2,4 = 4 10-3 mol/L conservation de A1 : [A1H] + [A1-] = 0,1 d où [A1H] = 0,1-4 10-3 =9,6 10-2 mol/L Ka = 4 10-3
* 4 10-3 / 9,6 10-2 =
1,67 10-4 ; pKa = -log
1,67 10-4 = 3,8.
A l'équivalence les quantités de matière des réactifs mis en présence sont en proportions stoechiomètriques c1v1 = c2v2 soit v2 = c1v1 / c2 = 0,1*50 / 0,1 = 50 mL la valeur du pH à l'équivalence est supérieure à 7, la base conjuguée A1- est très majoritaire. A la demi équivalence ( v'2 = 25 mL) de ce dosage le pH est égal au pKa du couple A1H/A1- : on obtient une solution tampon.
|
|||||||||||||||||||||||||
|
Plus de 50 % de la production mondiale de zinc est obtenu par électrolyse d'une solution de sulfate de zinc, acidifiée à l'acide sulfurique. Les ions sulfates ne participent pas aux réactions électrochimiques.. On observe un dépôt métallique sur une électrode et un dégagement gazeux sur l'autre. I- Etude de la transformation :
II- Exploitation : l'électrolyse a lieu sous 3,5 V. L'intensité du courant peut atteindre 80 kA. Après 48 H de fonctionnement, le dépôt de zinc est suffisamment épais. Il est alors séparé et fondu en lingots.
corrigé 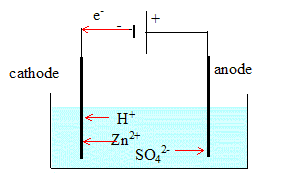
les réactions susceptibles de se produire sur chaque électrodes : à la cathode négative, réduction : Zn2+ (aq) + 2e- = Zn(s) majoritaire mais aussi 2H+ (aq) + 2e- = H2(g) à l'anode positive, oxydation : H2O (l)= ½O2 (g)+ 2H+ (aq) + 2e-. d'où l'équation globale de cette électrolyse : Zn2+(aq) + H2O(l) = Zn + ½O2(g) + 2 H+(aq) L'électrolyse est une transformation forcée qui nécessite un apport d'énergie électrique. vérification théorique : comparer le quotient initial et la constante d'équilibre .
Zn2+ (aq) + 2e- = Zn(s) d'où : la quantité de matière d'électrons n( e-) est égale à 2 fois la quantité de matière de zinc. n( e-) = 2x Quantité de matière d'électricité Q= 96000 n(e-) =96000*2 x = 1,92 105 x ordre de grandeur de la masse de zinc produite en 2 jours par une cellule : de plus Q= I t = 8 104 * 2*24*3600 = 1,38 1010 C d'où x = 1,38 1010 / 1,92 105 = 7,2 104 mol masse de zinc (g)= masse molaire (g/mol) * Qté de matière (mol) = 65* 7,2 104 =4,68 106 g = 4,68 t. on obtient une quantité de zinc inférieure à celle attendue : les ion H+ se réduisent également à la cathode. relation entre l'avancement x et le volume V de dioxygène récupéré : quantité de matière de O2 (mol) = volume (L) / volume molaire (L/mol) = V/24 = ½ x soit V= 12 x ordre de grandeur de V : 12*7,2 104 = 8,6 105 L = 8,6 102 m3. en tenant compte du rendement : 8,6 102*0,8 = 688 m3.
|
|||||||||||||||||||||||||
|
|