|
|
||||
|
||||
|
Dans une rue plane et rectiligne, un motard M démarre quand le feu passe au vert avec une accélération de valeur a1 pendant la durée S ; ensuite le pilote maintient sa vitesse constante de valeur v1. A l'instant du démarrage du cyclomoteur, une automobile A, située à la distance D du feu, derrière M, roule à vitesse constante , de valeur v2. On choisit comme origine des espaces, la position du feu tricolore, et comme origine des temps, l'instant où l'auto pase devant le feu tricolore. Le sens positif de l'axe correspond au ens du mouvement.
a1 = 1 m/s² ; v2 = 10 m/s ; D= 10 m ; 80½= 8,9 ; S = 20 s. corrigé nature du mouvement du motard pendant la première phase de son déplacement : mouvement rectiligne uniformément accéléré. La vitesse v est une primitive de l'accélération : v est de la forme a1 t ; soit en tenant compte de l'origine des dates : v = a1( t+T) la position xM du motard est une primitive de la vitesse : xM est de la forme ½a1t2 ; xM = ½a1( t+T)2 et en combinant ces deux relations ( éliminer le temps): v2 =2 a1xM . durée T nécessaire pour que A atteigne le feu : T= D/v2 = 10/10 = 1 s. équation horaire xM(t) du motard pout t<= S-T en fonction de a1, D et v2 : xM(t) = ½a1(T+t)2 = ½a1(D/v2+t)2 ; xM(t) = 0,5 (1+t)2 . équation horaire xA(t) de l'auto : xA(t) = v2 t = 10 t. date t1 à laquelle l'auto rattrape la moto : xA(t1)=xM(t1) 0,5(1+t1)2= 10 t1 ; t12 -18t1+1=0 deux solutions : t= 0,1 s et t= 17,9 s. à la date t= 0,1 s, la voiture dépasse la moto ; à la date t = 17,9 s, la moto dépasse à nouveau la voiture. Pour t>=S-T soit t> 19 s, la moto est en tête. position de la moto pour t= S-T soit t = 19 s : xM(19) = 0,5*20² = 200 m. équation horaire du motard pour t>=19 s : mouvement rectiligne uniforme à la vitesse v = a1S = 20 m/s.
|
||||
|
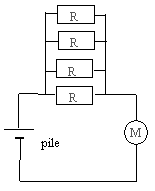
On dispose du matériel suivant : une pile "9 V", cinq conducteurs ohmiques de résistances R= 20 W, deux multimètres, des fils, un jouet ( petite grue doté d'un moteur électrique), une notice du moteur de la grue sur laquelle on peut lire " puissance électrique maximale tolérée = Pmax = 3 W". Tension aux bornes du moteur électrique U= E'+ r' I avec E' : force électromotrice du motuer et r': résistance électrique du moteur Etude de la pile : on réalise un montage qui permet de tracer la caractèristique intensité-tension de la pile, c'est à dire la courbe représentant l'évolution de la tension UPN aux bornes de la pile en fonction de l'intensité I qu'elle débite. 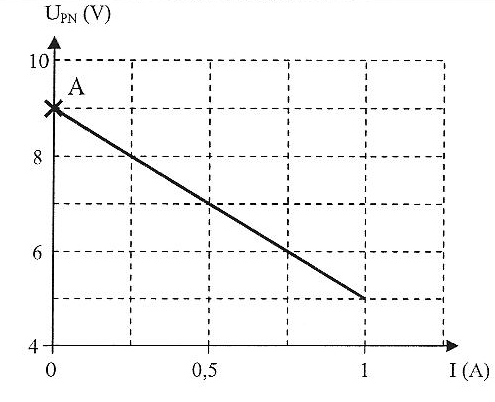
Etude du moteur de la grue : on décide de faire fonctionner le moteur grâce à la pile de 9 V.
Utilisation de la grue : une charge de masse m= 1 kg est posée au sol, à côté de la grue ; le fil indéformable est tendu. 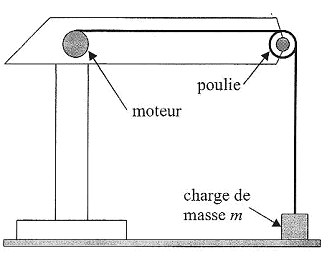 On fait tourner le moteur électrique pendant t= 5,0 s, ce qui a pour effet d'enrouler le fil sur l'arbre du moteur et ainsi de lever la charge d'une hauteur totale h= 75 cm. On considère que le mouvement de la charge est rectiligne et uniforme pendant la montée. L'intensité du courant dans le circuit vaut I= 0,5 A. g = 10 m/s².
valeurs de la fem E et de la résistance interne r de la pile : E= 9 V ( ordonnée du point A) pente de la droite :-4/1 = -4 V A-1 ; d'où r = 4 W. On relie brievement les deux bornes de la pile par un fil de jonction : UPN=0 soit Imax = E/r = 9/4 = 2,25 A. on monte en série la pile et deux conducteurs ohmiques
de résistance R : E-r I
= 2RI soit I = E/(2R+r) = 9/44 = 0,20
A.
Puissance absorbée par le moteur : P= UPN I= 6*0,75 = 4,5 W, valeur bien supérieure à 3W, Pmaxi que peut supporter le moteur : celui-ci va être grillé. on réaliser un dipôle ohmique de résistance R' = 5 W en branchant 4 résistors de résistance R= 20 W en dérivation.
tension aux bornes de la pile durant la montée de la charge : UPN= E-rI = 9-4*0,5 = 7 V. énergie électrique fournie par la pile en 5 s : UPN I t = 7*0,5*5 =17,5 J diminution d'énergie chimique contenue dans la pile : E I t = 9*0,5*5 = 22,5 J. expression de la puissance mécanique Pm que développe le moteur durant la montée : Mouvement rectiligne uniforme : les deux forces appliquée à la charge m ont la même valeur et sont opposées ( d'après le principe d'inertie ) Donc, la valeur absolue du travail du poids est égal au travail de la tension du fil : W = mgh Or la puissance (W) est égale au travail (J) divisé par la durée (s) ; d'où Pm = mgh/5 = 1*10*0,75 / 5 =1,5 W. expression de la fcem E' du moteur en fonction de Pm : E' = Pm / I = 1,5 / 0,5 = 3 V.
|
||||
|
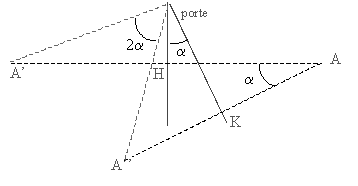
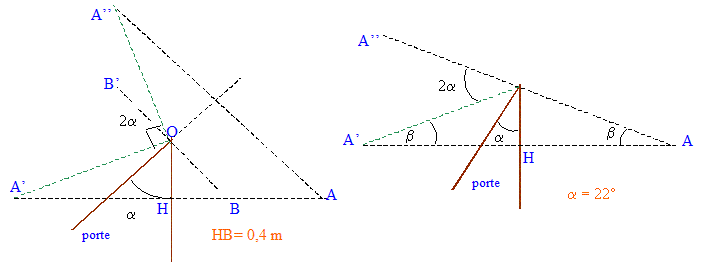
Une porte de 80 cm de large est recouverte d'un miroir. Un observateur situé à 1,00 m en face de cette porte fermée observe son image. Une autre personne ouvre la porte : le centre de la porte s'éloigne alors de l'observateur immobile qui perd rapidement de vue son image. En assimilant l'observateur à un point A situé sur la normale au plan de la porte fermée passant par son centre :
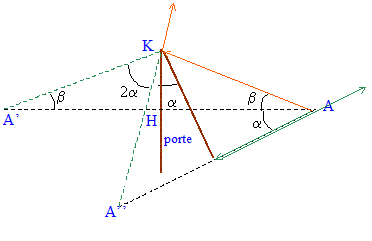
corrigé A' image de A quand la porte est fermée ( A et A' sont symétriques par rapport au plan de la porte) A'" image de A quand la porte est fermée ( A et A'' sont symétriques par rapport au plan de la porte)
Dés que l'image A" sort du champ visuel de l'observateur, ce dernier ne se voit plus dans le miroir.
tan b = 0,4/1 = 0,4 soit b =21,8 ° ; AK = (1² + 0,4²)½=1,077 m sin ( a+b) = 0,8 / 1,077 = 0,743 soit a+b = 48 ° ; d'où a = 48-21,8 = 26,2°.
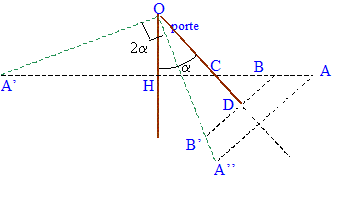
L'observateur doit venir en B afin de voir son image B'. Dans les triangles OHC et DBC : OC = 0,4*2½ =0,566 m ; CD= DB = 0,8-0,566 = 0,234 m CB = 0,234*2½ = 0,33 m soit HB= 0,4+0,33 = 0,73 m ouverture en sens contraire :
|
||||
|
Le carbonate de magnésium est un composé ionique de formule MgCO3 peu soluble dans l'eau. On essaie de dissoudre un peu de ce solide dans l'eau.
corrigé MgCO3 (s) = Mg2+(aq) + CO32-(aq) constante K associée à cette équation : K =[Mg2+][CO32-] = s² d'où s = (10-5)½ =10-2,5 = 0,3 10-2 = 3 10-3 mol/L. quotient de réaction initial correspondant à l'équation écrite en 1 : Q r i = [Mg2+]i [CO32-]i [CO32-]i = s = 3 10-3 mol/L ; n( Mg2+) = 3 10-3*0,1 + 1,0 10-3 =1,3 10-3 mol ; [Mg2+]i =1,3 10-3 / 0,1 = 1,3 10-2 mol/L Q r i = 3 10-3*
1,3 10-2 = 3,9 10-5
; Q r i >K, donc évolution dans le sens
indirect, de la droite vers la gauche.
n (Mg2+) total = m/84 +10-3 mol ; [Mg2+] = m/84 +10-3 mol /L ; [CO32-] = m/84 mol/L à l'équilibre : K= (m/84 +10-3 ) * m/84 ; on pose x = m/84 d'où x² + 10-3 x-10-5 = 0 ; retenir la solution positive x = 2,7 10-3 mol. |
||||
|
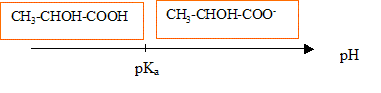
L'acide lactique a pour formule CH3-CHOH-COOH. On prépare 50,0 mL d'une solution aqueuse S d'acide lactique de concentration molaire cA= 2,00 10-2 mol/L. Le pH de cette solution vaut pH= 2,8.
zone de virage phénolphtaléine : incolore [8,2- 9,8] rose corrigé les groupes fonctionnels présents dans la molécule ; -COOH acide carboxylique ; C-OH : alcool secondaire. deux couples acide /base qui interviennent quand on dissout de l'acide lactique dans l'eau : CH3-CHOH-COOH / CH3-CHOH-COO- : CH3-CHOH-COOH = CH3-CHOH-COO- + H+. H3O+/H2O : H3O+= H2O + H+. équation de la réaction de l'acide lactique avec l'eau : CH3-CHOH-COOH + H2O = CH3-CHOH-COO- +H3O+. taux d'avancement final de la transformation : t = xfin / xmax. xmax = Ca*0,05 = 2 10-2*0,05 mol ; xfin = 10-pH*0,05 = 10-2,8*0,05 mol t = 10-2,8 / 2 10-2 = 0,5*10-0,8 = 0,5*0,16 = 0,08. La transformation est partielle car t <<1. domaines de prédominance de l'acide lactique et de son espèce conjuguée
à pH=2,8 la forme acide prédomine. A partir de la question 3: 8% de forme ion lactate et 92% de la forme acide lactique.
volume de solution d'hydroxyde de potassium à ajouter pour observer le changement de couleur : à l'équivalence les quantités de matière des réactifs mis en présence sont en proportions stoechiomètriques : CaVa = CbVb soit Vb = CaVa / Cb=0,02*20 / 0,05 = 8 mL. changement de couleur observé : dans l'erlenmeyer, avant l'équivalence, l'acide lactique est en excès ( solution incolore) ; après l'équivalence, les ions HO- sont en excès ( couleur rose).
|
||||
|
|