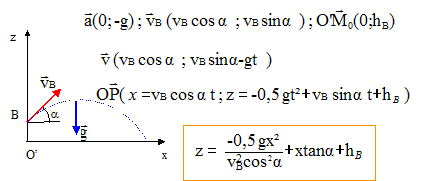|
|
|||
|
|||
|
|
|||
|
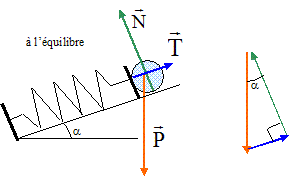
Un ressort de constante de raideur k, de masse négligeable et de longueur à vide l0 est fixé par l'une de ses extrémités à une butée fixe. Il peut osciller sans frottement suivant la ligne de plus grande pente d'un plan incliné d'un angle a par rapport à l'horizontale. On relie l'extrrémité libre du ressort à une petite bille de masse m. On considérera cette bille comme ponctuelle. A l'équilibre, le ressort est comprimé de 1,0 cm par rapport à sa longueur à vide et la bille se trouve en A. m= 200 g ; a= 20° ; yB= 14 cm ; AB= 20 cm. 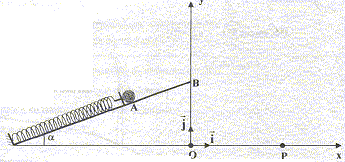
A l'équilibre T=kx=mgsina d'où k= mgsina / x = 0,2*9,8 sin20 / 0,01 = 67 N/m. vitesse vA( en m/s) de la bille en A. origine des énergies potentielles : le point A ( position d'équilibre). Ecrire la conservation de l'énergie mécanique. Au point le plus bas ( ressort comprimé de 8 cm suplémentaires, soit 9 cm en tout) l'énergie est sous forme potentielle élastique et de pesanteur 0,5*67*0,09²-0,2*9,8*0,08 sin 20 = 0,218 J En A, l'énergie est sous forme cinétique : ½mv²A 0,218 =½mv²A soit v²A=0,218*2/0,2 = 2,18; vA= 1,5 m/s. ( 1,476 m/s) vitesse vB( en m/s) de la bille en B : entre A et B seul le poids effectue un travail résistant ( l'action du plan, perpendiculaire au plan ne travaille pas) travail du poids : mg(yA-yB) = -mgAB sina = -0,2*9,8*0,2 sin 20 = -0,134 J théorème de l'énergie cinétique entre A et B : ½mv²B-½mv²A= -mgAB sina v²B=v²A - 2gAB sina = 2,18 -2*9,8*0,2*sin 20 = 0,84 ; vB= 0,92 m/s. calcul de OP en cm : chute libre avec vitesse initiale
en P l'altitude est nulle : 0 = -4,9 x²/(0,92²*cos²20) + x tan20 + 0,14 -6,56 x² + 0,364 x+0,14 = 0 d'où x = 0,176 m ( 18 cm) durée en seconde mise par la bille pour aller de A en P : trajet BP : OP=vBcosa t soit t =OP/(vBcosa)=0,176/(0,92*cos20)= 0,20 s. trajet AB : mouvement rectiligne uniformément retardé d'accélération a telle qie : v²B-v²A=2a AB soit a = (0,92²-1,5²) / 0,4 = -4,61 m/s. vitesse primitive de l'accélération : v= -at + vA = -4,61 t + 1,5 soit t =( vB -vA)/a=(1,5-0,92)/4,61 = 0,13 s total : 0,20+0,13 = 0,33 s.
|
|||
|
On comprime le ressort de 8,0 cm vers le bas depuis la position d'équilibre puis on lâche le système {bille ressort} sans vitesse initiale. Etablir l'expression de l'énergie mécanique du système {bille + ressort+ Terre} pour une position quelconque de la bille en contact avec le ressort ; en déduire l'équation différentielle du mouvement puis l'abscisse x(t) du centre d'inertie de la bille. corrigé expression de l'énergie mécanique du système {bille + ressort+ Terre} : origine des énergies potentielles : le point A ( position d'équilibre). Ecrire la conservation de l'énergie mécanique. Axe choisi : origine A, axe parallèle au plan, orienté vers le haut ; l'abscisse x(t) = x, du centre d'inertie de la bille est donc négative. énergie cinétique : Ec = ½mv² = ½mx'² énergie potentielle de pesanteur : Epp = mgh = mg x sin a. énergie potentielle élastique : Ep élast = ½k( l-l0)² = ½k( léqui-x-l0)² énergie mécanique du système {bille + ressort + Terre} :
Em= ½mx'² +
mg x sin a + ½k( léqui-x-l0)²
= constante.
Dériver par rapport au temps l'expression de l'énergie mécanique : mx' x" + mg x' sin a + k( léqui-x-l0)(-x') = 0 simplifier par x' : m x" + mg sin a - k( léqui-x-l0) = 0 or mg sin a = k( léqui-l0) d'où : m x" +kx=0. c'est l'équation différentielle d'un
oscillateurharmonique de pulsation w0
= (k/m)½.
solution de l'équation différentielle : x(t) = A cos (w0t + B) A et B sont déterminées par les conditions initiales ( vitesse initiale nulle et x(0) = -0,0 8 m -0,08 = A cos B d'où B= pet A= 0,08 m x(t) = 0,08 cos cos (w0t + p ) |
|||
|
|