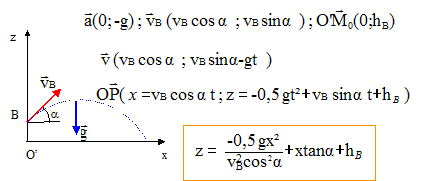optique.
- Un objet AB de hauteur 3 cm est placé devant
une lentille convergente de vergence 10 d.
L'objet, assimilable à un segment est
perpendiculaire à l'axe optique principal de la
lentille. A est situé sur l'axe optique, à
30 cm du centre optique O de la lentille.
Combien y a-t-il d'affirmations exactes ?
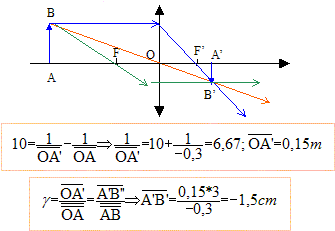
- Le foyer image F ' se trouve à 40 cm de A (
vrai)
- Le foyer image est le point où tous les rayons
qui sortent de la lentille convergent. (
faux)
- L'image A'B' est de même sens que AB (
faux)
- La taille de l'image A'B' est de 2 cm (
faux)
- L'image se trouve à 5 cm du foyer objet (
faux)
- On appelle pouvoir séparateur de l'oeil la
plus petite distance angulaire entre deux points
séparés par l'oeil. Pour un oeil normal,
cette distance angulaire vaut : e=
3 10-4 rad. On veur observer deux
cratères lunaires avec une lunette astronomique.
Distance des cratères : 30 km ; Distance
terre-lune = 3,8 105 km.
- Déterminer le grossissement minimal de la
lunette pour pouvoir distinguer les deux cratères.
(2 ; 4 ; 6 ; 8 ; 10 ; aucune réponse exacte)
Diamètre apparent des " deux cratères " =
30 / 3,8 105 = 7,9 10-5 rad, valeur
inférieure à e.
Grossissement minimum de la lunette : 3 10-4 /
7,9 10-5 = 3,8 ( soit
4)
- On considère une pile de fem E, de
résistance interne r, délivrant un courant
d'intensité I. Combien y a-t-il d'affirmations
exactes ?
- La tension aux bornes de la pile peut être
supérieure à sa fem E (
faux) " U= E-rI "
- La pile s'échauffe quand elle fonctionne
(vrai )
- La pile dissipe par effet joule pendant la durée
Dt une énergie
égale à : rI²Dt
(vrai )
- La tension aux bornes de la pile est proportionnelle
à l'intensité du courant qu'elle
délivre ( faux) " E-U
est proprotionnel à I"
- L'énergie électrique totale
délivrée par la pile pendant la
durée Dt se calcule par
la relation EI²Dt (
faux) " E I Dt
"
- On considère une pile de fem E= 12 V et de
résistance interne r= 0,8 W.
La puissance utile fournie par cette pile au reste du
circuit est Pu=5,4 W. Calculer
l'intensité du courant ( en A)
débité par cette pile.(0,12 ; 0,24 ; 0,37 ;
0,46 ; aucune réponse exacte )
tension aux bornes de la pile : U= E-rI=12-0,8 I
puissance utile P=UI = (12-0,8 I )*I ; 5,4 = 12 I -0,8
I² ; résoudre l'équation du second
degré : d'où I=
0,46
A.
- Un condensateur de
capacité C est initialement
déchargé. On l'associe en série avec
un résistor R. Cet ensemble est alimenté
par un générateur idéal de tension
continue de fem E= 14,0 V. A t=0 on ferme l'interrupteur
et on relève les variations de la charge q de
l'armature positive du condensateur en fonction du
temps.
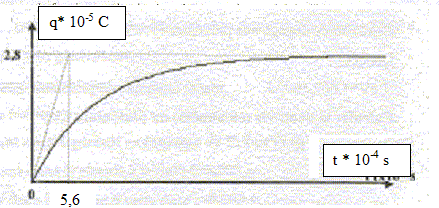
Déterminer la valeur de R
(ohms) (280 ; 420 ; 680 ; 920 ; 1200 ; aucune
réponse exacte)
[dq/dt]t=0 =I0 =
2,8 10-5 / 5,6 10-4 = 0,05 A
E = RI0 d'où R= 14/0,05 =280
W.

- Une corde est tendue par le
poids d'une masse m= 200 g; OB= 250 cm ; AP= 150 cm. On
montre que la célérité des ondes
transversales le long d'une corde est donnée par
la relation v=( F/m)½
avec F tension de la corde en N et m
masse par unité de longueur de corde. On produit
une brève secousse à
l'extrémité O de la corde. On
déclenche le chronomètre lorsque la
perturbation arrive au point A de la corde. On arr^te le
chronomètre lorsque la perturbation arrive au
point P et on lit Dt=
0,35 s. Déterminer la masse ( en kg ) de la
corde.(0,18 ; 0,27 ; 0,35 ; 0,56 ; 0,84 ; aucune
réponse)
AP= 1,5 m ; Dt=
0,35 s ; v = AP/Dt=1,5/0,35
= 4,286 m/s
F= mg = 0,2*9,8 = 1,96 N
m
= F/v² = 1,96 /
4,289² = 0,107 kg /m
masse de la corde : 0,107*2,5 =
0,27
kg.
- Un coup sec est appliqué
à une canalisation en acier dans laquelle circule
du pétrole. Un capteur situé à la
distance d=480 m du point d'application du coup,
enregistre deux signaux sonores très brefs
séparés par une durée
Dt=
224 ms. Vitesse de propagation du son dans l'acier
va= 5,00 km/s. Déterminer la vitesse (
en km/s) de propagation du son dans le pétrole.
(0,85 ; 1,20 ; 1,50 ; 1,70 ; 2,10 ; aucune bonne
réponse)
durée du parcours dans l'acier : ta =
d/ va= 0,48 / 5 = 0,096 s
durée du parcours dans le pétrole :
tp= d/vp = 0,48 / vp
Dt=tp-ta
; 0,224 = 0,48 / vp-0,096 ; 0,32 = 0,48 /
vp ; vp= 0,48/0,32
=1,5
km/s.
- A un
instant pris comme origine des temps on lance
vertcalement vers le haut un projectile d'un point
situé à 8,0 m au dessus d'une
rivière. Le projectile entre en contact avec l'eau
de la rivière 1,9 s plus tard. On néglige
l'action de l'air. Calculer la valeur de la vitesse ( en
km/h) avec laquelle on a lancé le projectile. (11
; 18 ; 21 ; 25 ; 27 ; aucune bonne réponse)
On choisi un axe vertical, orienté vers le bas ;
l'origine est le point de lancement : z = ½gt²
-v0t = 4,9 t² -v0t
au contact de la rivière z = 8 et t = 1,9
d'où : 8 = 4,9*1,9²-1,9 v0 ;
v0= 5,1 m/s ; soit 5,1*3,6 =
18
km/h.
- Titan décrit une orbite
circulaire de période T et de rayon r autour de la
planète Saturne. On admettra que Titan et Saturne
ont une répartition sphérique de
masse.
|
satellite
|
période T(en j)
|
rayon de l'orbite r ( en km)
|
|
Titan
|
15,94
|
1,222 106
|
G= 6,67 10-11 SI ; densité moyenne de
Saturne : d= 0,69.
Déterminer le diamètre ( en km) de
Saturne.( 5,8 104 ; 7,8 104 ; 9,2
104 ; 1,2 105 ; 1,9 105
; aucune bonne réponse)
3ème loi de Kepler :
T²/r3 = 4p²/(GMsaturne)
donne Msaturne = 4p²r3
/ (GT²) avec r = 1,222 109 m ; T=
15,94*24*3600 = 1,377 106 s. m
= 690 kg m-3.
Msaturne =
4*3,14²*(1,222
109)3 / (6,67
10-11*(1,377
106)2) =5,69
1026 kg.
Volume de Saturne : Msaturne / d = 5,69
1026 / 690 = 8,25 1023
m3.
4/3pR3saturne=
8,25 1023 d'où
R3saturne=1,97 1023 ;
Rsaturne=5,81 107 m = 5,81
104 km ; diamètre =
1,2
105 km
- Le plutonium
23894Pu est un émetteur
a
très puissant. Chaque désintégration
libère une énergie de 5,48 MeV. On
considère une source de masse m= 150 mg de
plutonium 238. Cette source dégage une puissance
P= 85 mW
1 eV= 1,6 10-19 J ; masse atomique du
plutonium 238 : 238,1 u ; 1 u = 1,661 10-27
kg.
Calculer la demi-vie ( en années ) du plutonium
238. ( 86 ; 128 ; 245 ; 412 ; 510 ; aucune bonne
réponse)
m = 1,5 10-4 kg et masse atomique du plutonium
= 238,1*1,6110-27= 3,954 10-25
kg
nombre initiaux de noyaux de plutonium : N0=
1,5 10-4 / 3,954 10-25 =3,79
1020.
activité initiale A0 = 0,085 / (5,48
*1,6 10-19)==9,69 1010 Bq
l=
A0 = / N0 = 9,69 1010
/3,79 1020= 2,56 10-10
s-1.
t½ = ln2 / l=
0,693 /2,56 10-10 = 2,7 109 s =
86
ans.
|
|
ressort
+
bille
Un ressort de constante de raideur k, de masse
négligeable et de longueur à vide
l0 est fixé par l'une de ses
extrémités à une butée fixe. Il
peut osciller sans frottement suivant la ligne de plus
grande pente d'un plan incliné d'un angle
a par rapport à
l'horizontale. On relie l'extrrémité libre du
ressort à une petite bille de masse m. On
considérera cette bille comme ponctuelle. A
l'équilibre, le ressort est comprimé de 1,0 cm
par rapport à sa longueur à vide et la bille
se trouve en A.
m= 200 g ; a= 20° ;
yB= 14 cm ; AB= 20 cm.
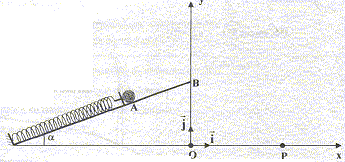
- Déterminer la constante de raideur k du
ressort.( en N/m).
On comprime le ressort de 8,0 cm vers le bas depuis la
position d'équilibre puis on lâche le
système {bille ressort} sans vitesse
initiale.
- Calculer la vitesse vA( en m/s) de la
bille en A.
On néglige les frottements entre A et B. La bille
quitte le ressort en A avec la vitesse
vA.
- Calculer la vitesse vB( en m/s) de la
bille en B.
La bille quitte le plan incliné en B avec la
vitesse vB. On néglige l'action de
l'air sur la bille. Le mouvement est étudié
dans le repère Oij. La bille touche le sol en
P.
- Déterminer OP en cm.
- Déterminer la durée en seconde mise par
la bille pour aller de A en P.
corrigé
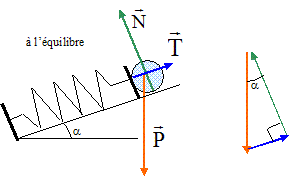
A l'équilibre
T=k(Léq-L0)
= mgsina
(1)
d'où k=
mgsina
/ (Léq-L0) = 0,2*9,8 sin20 /
0,01 = 67
N/m.
vitesse vA( en m/s) de la bille en
A.
origine des énergies potentielles : le point A (
position d'équilibre).
travail élémentaire résistant du
poids parcours noté dx : - mg
sina
dx
en tenant compte de
(1) : - mg
sina
dx =
-
k(Léq-L0)dx
travail élémentaire dW moteur de
la tension parcours noté dx :
T = k(L-L0) = k(L-Léq
+Léq-L0) =
k(L-Léq) +
k(Léq-L0)
dW= k(L-Léq)dx +
k(Léq-L0)dx
On note (L-Léq) = x : dW= kxdx +
k(Léq-L0)dx
somme des travaux élémentaires :
-
k(Léq-L0)dx
+ kxdx + k(Léq-L0)dx = kxdx
intégrer sur tout le parcours : W =
½kx2 =
½k(L-Léq)2.
Ecrire le théorème de l'énergie
cinétique entre le point le plus bas et A :
½k(L-Léq)2 =
½mv2 ; v =
(L-Léq)[k/m]½.
v= 0,08 [67/0,2]½=
0,218 =½mv²A
soit v²A=0,218*2/0,2 = 2,18; vA=
1,5
m/s.
( 1,464 m/s)
vitesse vB( en m/s) de la bille en B
:
entre A et B seul le poids effectue un travail
résistant ( l'action du plan, perpendiculaire au plan
ne travaille pas)
travail du poids : mg(yA-yB) =
-mgAB sina = -0,2*9,8*0,2 sin 20
= -0,134 J
théorème de l'énergie
cinétique entre A et B :
½mv²B-½mv²A= -mgAB
sina
v²B=v²A - 2gAB
sina
= 2,14 -2*9,8*0,2*sin 20 = 0,84 ;
vB=
0,92 m/s.
calcul de
OP en cm :
chute libre avec vitesse initiale
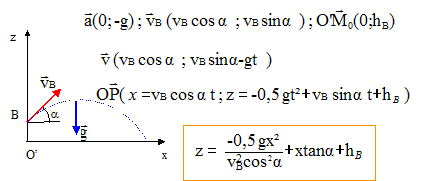
en P l'altitude est nulle :
0 = -4,9 x²/(0,92²*cos²20) + x tan20 +
0,14
-6,56 x² + 0,364 x+0,14
= 0 d'où x = 0,176 m ( 18
cm)
durée en seconde mise par la bille pour aller
de A en P :
trajet BP : OP=vBcosa
t soit t =OP/(vBcosa)=0,176/(0,92*cos20)=
0,20 s.
trajet AB : mouvement
rectiligne uniformément retardé
d'accélération a telle qie :
v²B-v²A=2a AB soit a =
(0,92²-1,5²) / 0,4 = -4,61 m/s.
vitesse primitive de
l'accélération : v= -at + vA =
-4,61 t + 1,5 soit t =( vB
-vA)/a=(1,5-0,92)/4,61 = 0,13 s
total : 0,20+0,13 =
0,33
s.
|
|
dipôle
RL
Un circuit est composé d'un
générateur de tension continue de fem E, d'une
bobine d'inductance L et de résiqtance r= 10
W, d'un interrupteur K et d'un
conducteur ohmique R. Un dispositif informatisé
permet de suivre les valeurs des tensions uAB et
uBC au cours du temps. La fermeture de
l'interrupteur est prise comme origine des temps.
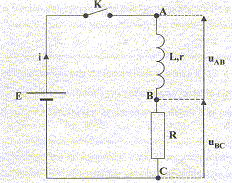
- Déterminer E.
- Calculer R et en déduire L ( en mH).
- Donner l'expression littérale de
l'intensité i du courant en fonction de L, R , E
et r. En déduire la valeur de l'intensité
à t= 0,003 s.
- Calculer la valeur de l'énergie stockée
par la bobine à t = 0,003 s.
corrigé
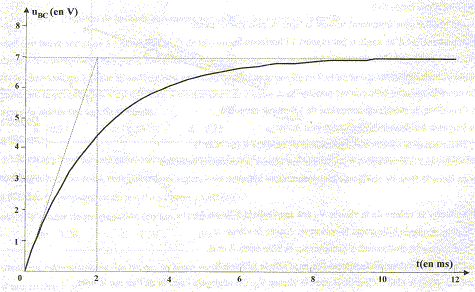
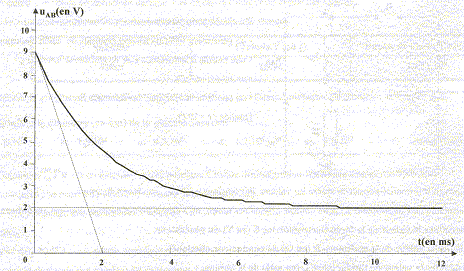
Déterminer E : uAB +
uBC= E avec uBC = Ri et uAB
= Ldi/dt + ri
en régime permanent di/dt=0 ; uBC = 7 V
; uAB =2 V soit E = 9
V.
Calculer R et en déduire L : en
régime permanent uBC = 7= RI ;
uAB =2 = rI soit I= 2/10 = 0,2 A ; R= 7/0,2 =
35 W.
R[di/dt]t=0 = 7/2 10-3 soit
[di/dt]t=0 =7/(2R 10-3) = 100
A/s ;
tension aux bornes de la bobine à t=0 : 9=
L[di/dt]t=0 =100 L d'où L= 9/100 =
0,09 H = 90 mH
ou bien à partir de la constante de temps
t du dipôle qui est
égale à 2 10-3 s ( lecture graphe)
; de plus t = L/(R+r)
d'où L= t (R+r) = 2
10-3*45 = 90 mH.
Expression littérale de l'intensité
i du courant en fonction de L, R , E et r :
uAB + uBC= E avec uBC =
Ri et uAB = Ldi/dt + ri
éq différentielle : E= Ldi/dt + (R+r) i
solution de la forme i(t) = A exp(-(R+r)t /L )+ B
à t = 0 l'intensité est nulle d'où
A+B=0 soit B=-A.
en régime permanent ( t <5 t)
: 0,2 = B = E/(R+r)
i(t) = E/(R+r)(1-exp(-(R+r)t /L
) = 0,2(1- exp(- t/2 10-3))
i(0,003) = 0,2 (1-exp (-1,5)) =0,155 A.
(155 mA)
valeur de l'énergie stockée par la
bobine à t = 0,003 s :
½Li² = 0,5*0,09*0,155² = 1,1
10-3 J = 1,1
mJ.
|