|
|
||||
|
||||
|
Les frottements seront négligés. Longueur à vide du ressort R1 : l0 = 10 cm ; raideur k1=k = 10 N/m ; la masse des ressorts est négligeable. g = 10 m/s² 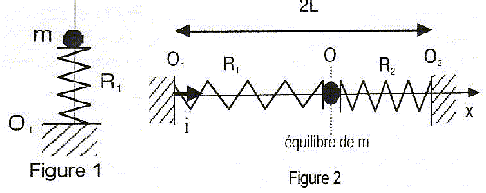 Partie A : ( figure 1) m = 40 g
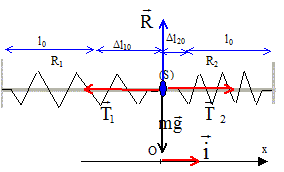
Partie B : ( figure 2) Longueur à vide du ressort R2 : l0 = 10 cm ; raideur k2=3k = 30 N/m ; la masse m coulisse le long de la tige O1O2= 2L= 30 cm. Soient Dl10 et Dl20 les allongements des ressorts R1 et R2 à l'équilibre.
corrigé 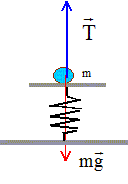
La masse m est soumise à son poids, vertical, vers le bas, valeur P= mg et à la tension du ressort, verticale, vers le haut, valeur T= k |Dl| A l'équilibre le poids et la tension du ressort se compensent. Ces deux forces opposées ont la même valeur mg = k(l-l0) = k |Dl| ; |Dl| = mg /k = 0,04*10 / 10 = 0,04 m = 4 cm. Dl = -0,04 m. Dl = l-l0 d'où l = Dl
+l0 = -0,04 +0,1 = 0,06 m.
action de la tige et poids se neutralisent. T1 = k1 Dl10 = k Dl10 ; T2 = k2 Dl20 = 3 kDl20 . A l'équilibre, ces deux forces ont la même valeur, d'où : Dl10 = 3Dl20 . de plus 2L= 2 l0 + Dl10+ Dl20 ; L= l0 +2 Dl20 ; Dl20 =½(L-l0) = 0,5(15-10)=2,5 cm = 0,025 m ; Dl10 =0,075 m. allongements Dl1 et Dl2 des ressorts : Dl1 = Dl10 +x ; Dl2 =Dl20 -x Ecrire la seconde loi de Newton projetée sur l'axe Ox avec : T1 = -kDl1 ; T2 = 3kDl2 . -k(Dl10 +x ) + 3k(Dl20 -x)= mx" (dérivée seconde de x par rapport au temps) -kDl10-kx + 3kDl20-3kx= mx" ; or kDl10=3kDl20 d'où -4kx = mx" soit x"+4k/m x=0. en posant w0²= 4k/m =40/0,04 = 1000 ; w0 =31,6 rad/s, l'équation différentielle s'écrit : x"+w0²x=0 (1) périodeT0 = 2p/w0 = 6,28 / 31,6 = 0,2 s. les solution de cette équation sont du type x(t) = A cos( 2p/T0 t+F). dériver deux fois par rapport au temps : x" = -( 2p/T0 )2 A cos( 2p/T0 t+F)= - w0²x repport dans (1) : - w0²x + w0²x=0 quel que soit le temps, donc x(t) = A cos( 2p/T0 t+F) est bien solution de (1) On détermine A et F par les conditions initiales : à t=0, x(0) = a = 0,02 m d'où 0,02 = A cos F ; d'où A=0,02 m et F =0 ( amplitude)
|
||||
|
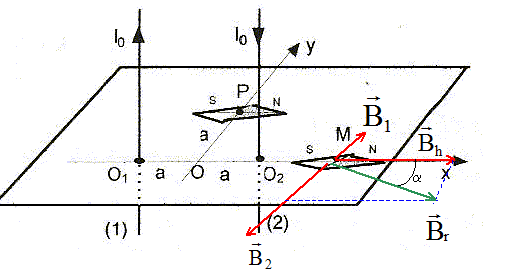
Soient deux fils rectilignes verticaux, infinis, parallèles situés à la distance O1O2 = 2a l'un de l'autre et parcourus par des courants de sens opposé et de même intensité I0. Le plan des deux fils est contenu dans le plan du méridien magnétique terrestre et une aiguille aimantée placée en leur voisinage s'oriente comme sur la figure lorsqu'aucun courant ne traverse les fils. 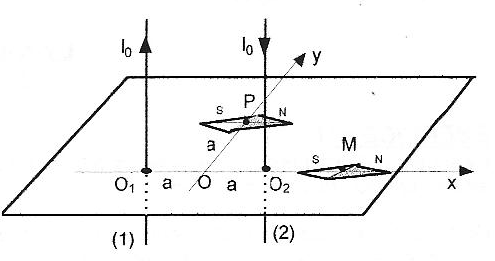 On rappelle qu'un fil rectiligne infini, parcouru par un courant crée en un point M' de l'espace un champ magnétique de valeur B= m0 I/ (2pr), où r est la distance de M' au fil. m0 = 4p 10-7 SI ; 2a = 20 cm ; Bh= 2 10-5 T, composante horizontale du champ magnétique terrestre.
corrigé Bh= m0 I0/ (2pa) soit I0 =2paBh/ m0 =2p *0,1*2 10-5 /(4p 10-7 )= 10 A. normes B1 et B2 des champs crée en M par les deux fils : O1M=3a et O2M= a B1= m0 I0/ (2p*3a) =Bh/3 ; B2= m0 I0/ (2pa) =Bh.
Br2 =Bh2 +(2/3Bh)2 =13/9 Bh2 ; Br =13½Bh/3 tan a =
(2/3Bh) / Bh = 2,/3 =
0,67 ; a =33,7 °.
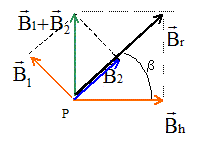
Pythagore : O1P2+ O2P2 =4 a² = O1O22 , donc le triangle PO1O2 est rectangle en P. normes B1 et B2 des champs crée en P par les deux fils : B1=B2= m0 I0/ (2p*2½a) =Bh/2½. schéma en vue de dessus :
Valeur du champ résultant : Br=2½Bh ; tan b = Bh / Bh = 1 ; b =45 °. l'aiguille aimantée tourne de 45°. |
||||
|
Masse du noyau de 20881 Tl : m(208 Tl)= 207,937 592 u ; masse du noyau d'hélium : m(4He)= 4,001 54 u ; Energie de liaison par nucléon : E(212 Bi) = 7,800 MeV/nucléons ; E(208 Tl) = 7,847 MeV/nucléons ; E(4 He) = 7,066 MeV/nucléons ; 1 u= 1,661 10-27 kg = 931,5 MeV c-2. corrigé composition du noyau de 21283 Bi : 83 protons ; 212-83 = 129 neutrons énergie de liaison d'un noyau : c'est l'énergie libérée lors de la formation du noyau à partir des nucléons séparés au repos. 21283 Bi-->20881 Tl + 42He. conservation de la charge : 83 = 81+2 ; conservation du nombre de nucléons : 212 = 208+4. énergie W libérée par cette réaction nucléaire : W = 4 E(4 He) + 208 E(208 Tl) -212 E(212 Bi) W= 4*7,066 +208*7,847-212*7,8 = 6,84 MeV. soit |Dm| =6,84/931,5 = 7,343 10-3 u masse du noyau de bismuth 212 : |Dm| = m(212 Bi) -(m(208 Tl) + m(4He)) m(212 Bi)=|Dm| + m(208 Tl) + m(4He) =7,343 10-3 +207,937 592 + 4,001 54 = 211,946 47 u. présence de ce rayonnement : le noyau fils se trouve dans un état excité ; le retour à l'état fondamental s'accompagne de libération d'énergie sous forme de photon g. énergie cinétique de la particule a : 6,84 -0,117-0,327 = 6,4 MeV.
|
||||
|
La solubilité s d'un cristal ionique est la concentration molaire volumique maximale en soluté apporté que l'on peut dissoudre dans 1 L de solution. L'eau de chaux est une solution aqueuse saturée d'hydroxyde de calcium Ca(OH)2. A 20,0°C, la conductivité de cette solution est s = 5,00 10-1 S/m
conductivité de la solution : s = lHO-[HO-] + lCa2+[Ca2+ ] = (2lHO-+ lCa2+) s s = s /(2lHO-+ lCa2+) = 0,5 /((2*190+120)10-4) = 5000/500= 10 mol m-3 = 1,00 10-2 mol/L pH de la solution d'eau de chaux : [H3O+]= Ke/[HO-]= 10-14 / 2 10-2 = 5 10-13 mol/L ; pH = -log( 5 10-13 ) =12,3. constante Ks de l'équilibre de dissolution de l'hydroxyde de calcium : Ks = [Ca2+ ][HO-] 2 = s (2s)² = 4s3= 4*( 10-2 )3 = 4 10-6.
|
||||
|
L'acétate de benzyle de formule CH3-COO-CH2-C6H5 est l'un des constituants de l'essence de jasmin.
corrigé équation chimique de sa formation à partir de l'acide éthanoïque : CH3-COOH + HO-CH2-C6H5 = CH3-COO-CH2-C6H5 + H2O caractéristiques de cette réaction : lente, athermique, limitée par l'hydrolyse de l'ester. rendement de cette synthèse : Quantité de matière (mol) = mase (g) / masse molaire (g/mol) n( acide) = 6/60 = 0,1 mol ; n( alcool) = 10,8 / 108 = 0,1 mol ( proportions stoechiométriques ) n( ester ) théorique si réaction totale = 0,1 mol soit 15 g rendement = masse réelle / masse théorique *100 = 10 /15 *100 = 66,7 %. Le rendement n'et pas amélioré ni par chauffage du
milieu réactionnel , ni par addition d'acide sulfurique. La vitesse de
la réaction augmente avec la température ; l'acide sulfurique sert de
catalyseur : on atteint donc plus rapidement l'équilibre, sans modifier
la composition de ce dernier.
CH3-COO-CH2-C6H5 + H2O = CH3-COOH + HO-CH2-C6H5 . Quantité de matière (mol) = mase (g) / masse molaire (g/mol) n( ester) initiale = 7,5/150 = 0,05 mol ; n( eau) initiale = 0,9/18 = 0,05 mol ( conditions stoehiomètriques) A l'équilibre 33% d'ester a réagi en donnant : 0,05/3 = 1,67 10-2 mol d'acide acétique et 1,67 10-2 mol d'alcool benzylique. Il reste 3,33 10-2 mol d'ester et
3,33 10-2 mol d'eau.
Cette hydrolyse basique de l'ester ou saponification est lente mais totale. n( ester) initiale = 1,5/150 = 0,01 mol ; donc 0,01 mol de soude est nécessaire soit un volume V (L) = quantité de matière (mol/ concentration (mol/L) = 0,01/10 = 10-3 L = 1 mL.
|
||||
|
|