d'après
concours
manipulateur électroradiologie médicale AP Paris 2005
|
|
|
|
|
|
|
|
|
QCM au
minimum une réponse exacte par question ( réponse en rouge souligné)
Dipôle RLC
- On charge un
condensateur sous une tension U à travers une résistance R=10 kW. A l'aide d'un oscilloscope oinn visualise
les tensions ci-dessous :
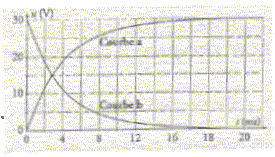
La courbe
représentant les variations de la tension uc aux
bornes du condensateur en fonction du temps est la courbe b. faux
Lors
de la charge la tension aux bornes du condensateur est croissante (
courbe a).
- La constante
de temps t est la durée au bout de laquelle le
condensateur est complétement chargé. faux Le
temps de charge est voisin de 5t=5RC ;
- La valeur
maximale de l'intensité traversant le circuit est 3 mA. vrai
Imax = U/R=30/10000= 3
10-3A = 3mA
- On charge
deux condensateurs identiques en série sous la tension U. L'énergie
emmagasinée dans chaque condensateur est le quart de celle qu'elle
aurait été avec un seul condensateur chargé sous la même tension U vrai
I.
E=½CU² pour un seul condensateur chargé sous
la tension U. En fin de charge la tension aux bornes de chaque
condensateur est ½U ; l'énergie est proportionnelle au carrée de cette
tension
- On branche
en série un générateur de fem E0=6V, un
interrupteur K, un conducteur ohmique R= 500 W et une bobine de résistance négligeable,
d'inductance L ( L=0,2 H). A l'instant t0=0 on
ferme l'interrupteur K.
- L'équation différentielle vérifiée pa r la tension U aux bornes du
générateur est : E0=Ldi/dt + Ri . vrai La
tension aux bornes du générateur est constante égale à E0.
Il s'agit plutôt de l'équation différentielle vérifiée par l'intensité.
La relation liant les tensions aux bornes des dipôles est celle
proposée.
- La solution de cette équation différentielle est : i=E0/R
exp(-t/t) faux
i=E0/R
[1-exp(-t/t)].
- La constante de temps est définie par t = R/L ; f aux t =L/R
.
- Cette constante de temps vaut : 0,2/500 = 4 10-4
s. vrai
|
|
|
Mécanique
: chute verticale (4
pts)
Un enfant lance vers le haut une bille de masse m=30 g.
A une hauteur h=1,40 m au dessus du sol, sa vitesse est de 3m/s par
rapport au sol. On néglige la résistance de l'air.
- Calculer l'énergie mécanique du système {bille-Terre}
en prenant l'origine de l'énergie potentielle au sol.
- Jusqu'à quelle hauteur la bille va-t-elle monter ?
- Avec quelle vitesse va-t-elle repasser à l'altitude
h=1,40 m ?
- Avec quelle vitesse va-t-elle atteindre le sol ? g=
9,8N/kg.
corrigé
énergie
mécanique = énergie cinétique + énergie potentielle de
pesanteur
EM=
½mv²+mgh = m(½v²+gh) = 0,03(0,5*3²+9,8*1,4)= 0,5446 ( 0,55 J)
Lorsque la hauteur
maximale est atteinte, l'énergie mécanique est sous forme
potentielle de pesanteur ; de plus l'énergie mécanique se conserve d'où
:
EM=
mghmax ; hmax =EM/(mg)
= 0,5446/(0,03*9,8)=1,86 m
La bille repasse à l'altitude h=1,4 m
avec la même vitesse v = 3 m/s.
écrire le théorème de l'énergie cinétique entre chaque
passage à l'altitude h=1,4 m ( montée et descente) : le poids ne
travaille pas , les altitudes de départ et d'arrivée sont identiques.
½mv²-½mv1²=0 d'où v=v1.
vitesse au sol lors de la descente :
au sol l'énergie mécanique est sous forme cinétique ; l'énergie
mécanique se conserve
½mv0² = EM soit v0²
= 2EM/m =0,5446*2/0,03 = 36,3 ; v0
= 6,02 ( 6,0 m/s).
|
|
Bore ( 4
pts)
Un noyau de bore ( 105B)
peut capter un neutron pour former un noyau de lithium73Li
- Ecrire l'équation bilan de cette réaction en
précisant les lois qui la régit. Quelle est la seconde particule formée
?
- Effectuer le bilan énergétique, puis calculer en MeV
et en J l'énergie libérée au cours de cette réaction.
- Quelle serait l'énergie libérée par la réaction
complète de 1 g de bore ?
- Avec quelle masse d'essence obtiendrait-on la même
quantité d'énergie par combustion ?.
masse en u : m(bore) = 10,012 94 ; m(lithium) =7,016 00 ; m(hélium) =
4,0026 ; m(neutron) = 1,008 67
1 u =1,67 10-27 kg ; NA=
6,02 1023 mol-1 ; MB=
10 g/mol ; pouvoir calorifique de l'essence 5 107
J/kg.
corrigé
105B
+ 10n --->AZX
+73Li
lois de conservation : conservation
de la charge : 5 = Z+3 soit Z=2 ( élément hélium)
conservation du nombre de nucléons : 10+1=A+7 soit A= 4
La seconde particule est un noyau d'hélium ou particule
alpha 42He
énergie libérée par la réaction d'un
atome debore :
Dm=
m(lithium) + m(hélium) - m(bore)- m(neutron) = 7,016 + 4,0026 - 10,012
94- 1,008 67 = -0,003 u
puis -0,003*1,6 10-27 = 5,027 10-30
kg
E= |Dm|c²
= 5,027 10-30*(3108)²
=4,52 10-13 J ou 4,52 10-13
/1,6 10-19 = 2,82 106 eV=
2,82 MeV
énergie libérée par la réaction complète de 1 g
de bore
E*NA/M(bore) = 4,52 10-13
* 6,02 1023 / 10 = 2,72 1010
J.
masse d'essence : 2,72 1010 /5107
= 544 kg.
|
|
pile
(4
pts)
On considère une pile constituée de deux électrodes de
cuivre plongeant chacune dans des solutions de sulfate de cuivre de
concentrations différentes. Chaque solution a un volume de 100 mL et
les concentrations initiale en ion cuivre II est [Cu2+]1=1,0
mol/L et [Cu2+]2=1,0 10-2
mol/L.
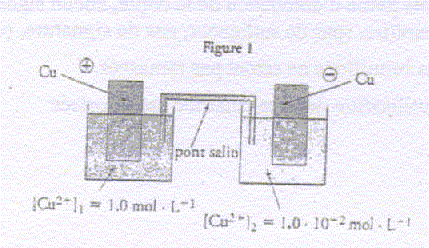
- Ecrire les demi-équations des réactions se produisant
aux électrodes en accord avec la polarité donnée sur la figure
ci-dessus.
- Donner le nom de chaque réaction.
- Ecrire l'équation de la réaction s'effectuant dans la
pile. Pour la réaction considérée la constante d'équilibre vaut K=1.
- Calculer la valeur du quotient initial Qr i.
Cette valeur est-elle cohérente avec la polarité proposée ?
- On fait débiter la pile dans un conducteur ohmique et
un ampèremètre. Compléter la figure et indiquer par des flèches le sens
du courant et le sens de déplacement des électrons dans le circuit
extérieur.
- Que peut-on dire des concentrations finales quand
l'état d'équilibre est atteint ?
corrigé
demi-équations
des réactions se produisant aux électrodes :
compartiment 1 : à la
cathode positive, réduction : Cu2+ + 2e-
= Cu ;
compartiment 2 : à
l'anode négative oxydation : Cu = Cu2+ + 2e-
bilan : (Cu2+)1
+ Cu = (Cu2+)2+Cu.
quotient initial Qr i =[Cu2+]2
i / [Cu2+]1 i=0,01/1
= 0,01, valeur inférieure à K, donc évolution spontanée dans le sens
direct, de la gauche vers la droite, en accord avec la polarité
proposée.
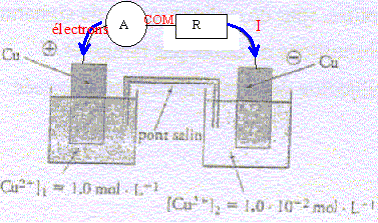
concentrations finales quand l'état
d'équilibre est atteint : Qr
f = K = 1 = [Cu2+]2 f /
[Cu2+]1 f ; [Cu2+]2
f = [Cu2+]1 f
les concentrations
finales sont égales. ( dans la mesure ou il y a
suffisamment de cuivre métal dans le compartiment 2)
|
L'éthanoate de
3-méthylbutyle
(4 pts)
- L'éthanoate de 3-méthylbutyle est utilisé comme arôme
de banane dans certains sirops. La formule semi-développée de ce
composé C est :
CH3-COO-CH2-CH2-CH(CH3)2.
Nommer la fonction chimique de ce composé.
- Le composé C est obtenu par réaction d'un acide
carboxylique A et d'un alcool primaire B. Ecrire la formule
semi-développée de A et B et nommer A et B.
Ecrire l'équation de la réaction entre A et B.
Quel est le nom de la réaction chimique entre A et
B, quelles sont ces caractéristiques ?
- Pour préparer cet arôme, on introduit 0,5 mol de A,
0,5 mol de B et 2 mL d'acide sulfurique concentré. On chauffe à reflux
pendant une heure, on refroidit le mélange réactionnel.
On prélève en cours de réaction, à intervalles
réguliers, un échantillon du mélange réactionnel que l'on dose. On note
l'évolution du nombre de moles du réactif A noté nA.
Les courbes 1,2 et 3 ne correspondent pas à l'expérience. Expliquer
pourquoi.
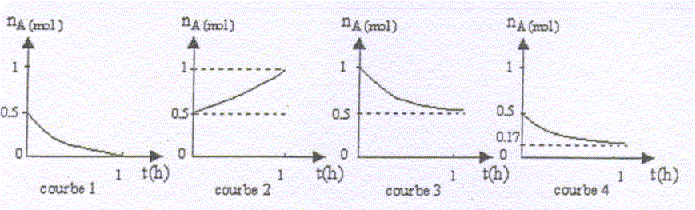
En utilisant les informations lues sur le graphique
correspondant à l'expérience réalisée, calculer le rendement de la
réaction.
La valeur du rendement varie t-elle : en prolongeant
la durée du chauffage ; en augmentant la température ; en augmentant la
quantité de matière du composé A. Justifier les réponses.
corrigé
fonction
chimique de ce composé : fonction ester -COO-C
A : acide éthanoïque CH3-COOH ; B
: (CH3)2CH-CH2-CH2OH
: 3-méthylbutan-1-ol
CH3-COOH + (CH3)2CH-CH2-CH2OH
= CH3-COO-CH2-CH2-CH(CH3)2
+ H2O
estérification lente, athermique, limitée par
l'hydrolyse de l'ester.
Les courbes 1, 2 et 3 ne correspondent pas à
l'expérience :
1 : à la fin le graphe indique nA=0,
or l'estérification est limitée par l'hydrolyse de l'ester et à
l'équilibre il reste de l' acide.
2 : le graphe indique une augmentation de nA;
or la quantité de matière d'un réactif décroît au cours du temps.
3 : le graphe indique nA= 1 mol
au départ au lieu de 0,5 mol ; de plus la réaction est limitée et la
quantité finale d'acide ne peut pas être égale à 0,5 mol.
rendement de la réaction ( graphe 4)
quantité de matière finale d'ester / quantité théorique
d'ester ( si réaction totale) *100
soit (0,5-0,17) / 0,5 *100 = 66 %.
La valeur du rendement ne varie pas en prolongeant la
durée du chauffage, dans la mesure ou l'équilibre est atteint.
La valeur du rendement ne varie pas en augmentant la
température ; l'équilibre est etteint plus rapidement.
La valeur du rendement augmente en augmentant la
quantité de matière du composé A ou B : l'équilibre est alors déplacé
dans le sens de la consommation du réactif A ou B introduit en excès ;
la quantité d'ester augmente, équilibre déplacé dans le sens direct.
|
|
retour
-menu
|



