Aurélie 05/06
Champ magnétique : solénoïde, Faisceau d'électrons

d'après concours manipulateur électroradiologie médicale Lyon, AP Paris,

Google

Etude du champ magnétique au centre d'un solénoïde

Pour différentes intensités I du courant dans trois solénoïdes de même longueur L, les mesures du champ magnétique B ( mT) au centre de ces derniers ont permis de tracer les graphes suivants :

  1. Pour chaque solénoïde montrer que B= k I et déterminer la valeur de k.
  2. Tracer la coube représentative de k en fonction de N, nombre de spires du solénoïde. Conclure.
  3. On effectue la même série de mesures en doublant la longueur L de chaque solénoïde. On constate que la valeur de B est divisée par deux. Comment varie B en fonction de la longueur L ?
  4. Parmi les relations suivantes quelle est celle qui conviendrait au calcul de B ? Justifier.
    B= k'NI ; B= k'IL/N ; B= k'NI/L ; B= k'LN/I, k' est une constante.
corrigé
Les trois graphes sont des droites passant par l'origine : le champ et l'intensité du courant sont proportionnelles soit B= k I avec k, constante de proportionnalité.

k1 = 10-3 / 3 = 3,33 10-4 T A-1 ; k2 = 2,5 10-3 / 4 = 6,25 10-4 T A-1 ; k3 = 5 10-3 / 4 = 12,5 10-4 T A-1 ;

coube représentative de k en fonction de N, nombre de spires du solénoïde ( k a été multiplié par 103 sur le graphe)

k et N sont proportionnels ; de plus B= kI d'où B= k'NI ( k' = constante)

le champ B et la longueur du solénoïde L sont inversement proportionnels : quand l'un double, l'autre est divisé par 2.

B= k'NI / L convient car :
- B et I sont proportionnels ; B et N sont proportionnels ; B et L sont inversement proportionels.

Faisceau d'électrons (4,5 pts)

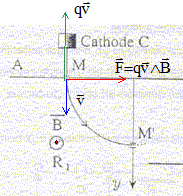
 Une cathode C est portée à haute température et émet des électrons à une vitesse négligeable devant toutes les vitesses considérées dans l'exercice. Le faisceau d'électrons émis par cette cathode est accéléré par une anode A. La différence de potentiel entre la cathode et l'anode est UAC. Le faisceau d'électrons traverse l'anode par un petit trou M et pénètre dans un région où règne un champ magnétique perpendiculaire au plan de la figure. Le faisceau d'électrons décrit un quart de cercle et pénètre dans un espace R2 sans champ magnétique où règne un champ électrique uniforme crée par l'électrode E. Le potentiel de cette électrode est inférieur à celui de l'anode A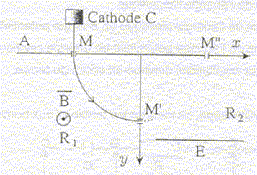

  1. Déterminer l'expression littérale de la vitesse des électrons en M. Calculer v.
  2. Déterminer le sens du champ magnétique.
  3. Montrer que l'expression du rayon de la trajectoire dans la région R1 est de la forme R= mv/(|q|B)
  4. Déterminer l'équation horaire des électrons dans la région R2. Quel doit être la valeur du champ électrique pour que les électrons passent en M" ?
    masse de l'électron m=9,1 10-31 kg ; charge de l'électron q= - 1,6 10-19 C ; UAC= 1000 V ; OM=OM'=OM"=R=10 cm
corrigé
expression littérale de la vitesse des électrons en M : le poids des électrons est négligeable ; la vitesse initiale est négligeable;

seule la force électrique effectue un travail, moteur, de valeur |q|UAM.

écrire le théorème de l'énergie cinétique entre C et M : ½mv²=|q|UAM ; v² = 2|q|/m UAM

v = ( 2|q|/m UAM)½ =(2*1,6 10-19 / 9,1 10-31 * 1000)½ =1,88 107 m/s.

sens du champ magnétique : vers l'avant

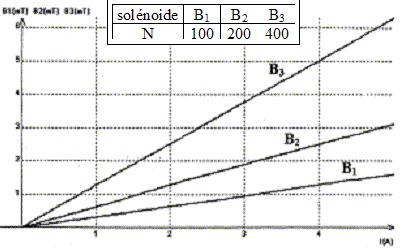
expression du rayon de la trajectoire dans la région R1 :

l'électron n'est soumis qu'à la force magnétique centripète dirigée vers le centre de l'arc de cercle.

La seconde loi de Newton s'écrit suivant l'axe n de la base de Frenet : |q|vB=mv²/ R soit R= mv/(|q|B)

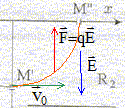
équation horaire des électrons dans la région R2 :

les électrons ne sont soumis qu'à la force électrique ; écrire la seconde loi de Newton : d'où l'accélération : ( 0 ; qE/m ) dans le repère (Ox, Oy)

la vitesse est une primitive de l'accélération : ( v0 ; qE/m t )

la position est une primitive de la vitesse : x = v0 t ; y = ½qE/m t²+R

t = x/v0 ; repport dans y : y = ½q/m E / (v0²) x² +R

en M" : x=R et y=0 d'où : ½qE / (mv0²) R² +R = 0 ; -½qE / (mv0²) R =1 ; ½|q|E / (mv0²) R =1

E= 2mv0²/ (|q|R) = 2*9,1 10-31(1,88 107 )² /( 1,6 10-19 *0,1) = 4 104 V.
retour -menu