Aurélie 20/12/05
cycle thermodynamique d'une machine à vapeur ;

production et utilisation des RX pour l'étude d'un cristal

d'après bts chimie 2005

Google

cycle thermodynamique d'une machine à vapeur

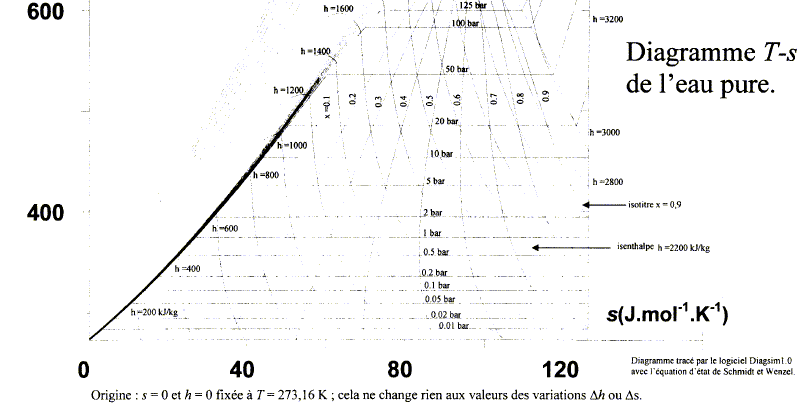
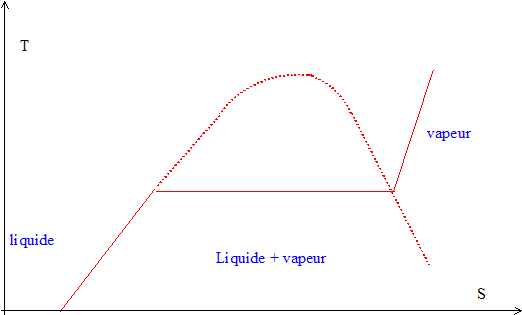
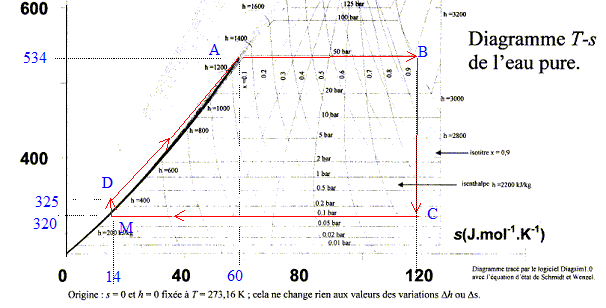
Le fonctionnement d'une machine à vapeur peut être modélisé par un cycle de Rankine. Un fluide, l'eau subit des transformations dont certaines consistent à réaliser des échanges thermiques avec deux sources de chaleur, chaque source étant à température constante. Ces échanges peuvent provoquer des transitions de phase liquide <--> vapeur.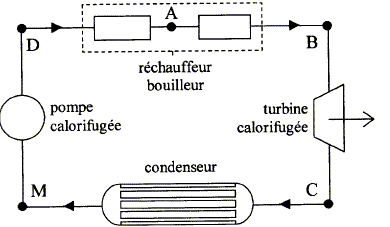

- vaporisation A--> B à pression constante P1= 50 bar du fluide dans le bouilleur.

- détente isentropique B--> C de la vapeur juste saturante dans la turbine calorifugée ( lors de cette étape de l'énergie est fournie sous forme de travail à l'extérieur de la machine à vapeur), jusquà P2<P1.

- condensation totale C--> M à pression constante P2 = 0,1 bar dans le condenseur.

- compression isentropique M--> D du liquide juste saturant au départ, de P2 à P1, dans la pompe calorifugée.

- échauffement D-->A à pression constante P1.

Etude du cycle :

  1. Indiquer quelle information donnée dans la description du cycle permet de conclure que la vaporisation est complète en B.
    Le diagramme T-s fourni permet de visualiser l'évolution de l'eau au cours du cycle. On peut voir sur ce diagramme la courbe de saturation ( courbe de rosée et courbe d'ébullition se rejoignent au point critique ), qui délimite la zone "état liquide", la zone " état vapeur" et la zone "coexistence liquide vapeur". On remarquera également la continiuté des courbes isobares et isenthalpes sur tout le domaine représenté, avec parfois une ou deux ruptures de pente.
  2. Indiquer sur le diagramme où sont situées les zones " état liquide", "état vapeur" et "coexistence liquide vapeur".
  3. En observant les courbes isobares du diagramme T-s, expliquer pourquoi on peut admettre que le point M est pratiquement confondu avec le point D sur ce diagramme, bien que les états D et M soient différents.
  4. Dessiner précisément le cycle de Rankine sur le diagramme fourni.
  5. Par lecture graphique, compléter le tableau suivant :

    état
    A
    B
    C
    M
    D
    P (bar)
    50
    50
    0,10
    0,10
    50
    T(K)

    h( kJ kg-1)
    1324
    3018
    2075
    235
    239
    s (J K-1 mol-1)

    14
    On rappelle l'expression du premier principe de la thermodynamique pour un fluide en écoulement permanent entre une entrée et une sortie de machine sans variation d'énergie cinétique ni variation d'énergie potentielle : Dh=hsortie-hentrée= W+Q
    ( h, W, Q grandeurs massiques ; W : travail utile fourni par la machine)
  6. Calculer l'énergie thermique ( ou quantité de chaleur) QDB reçue par 1,00 kg de vapeur d'eau, au cours du transfert thermique avec la source chaude.
  7. Calculer le travail reçu WBC dans la turbine calorifugée. Commenter son signe.
  8. Calculer le travail reçu WMD à la pompe calorifugée.
  9. Calculer l'énergie thermique Qf reçue par 1,00 kg d'eau lors du transfert thermique avec la source froide.
  10. Calculer le rendement h de ce cycle moteur.
quelques idées
La pression de vapeur saturante est la pression à laquelle un fluide passe de l'état gazeux à l'état liquide (ou l'inverse) à une température donnée.

information donnée dans la description du cycle permettant de conclure que la vaporisation est complète en B : " détente de la vapeur juste saturante dans la turbine calorifugée"

on peut admettre que le point M est pratiquement confondu avec le point D sur ce diagramme : un liquide est pratiquement incompressible

état
A
B
C
M
D
P (bar)
50
50
0,10
0,10
50
T(K)
534
534
320
320
325
h( kJ kg-1)
1324
3018
2075
235
239
s (J K-1 mol-1)
60
120
120
14
14
vaporisation A--> B à pression constante : Dh= 3018-1324 = 1694 kJ kg-1 ; Ds= 120-60 = 60 J K-1 mol-1

dans 1000 g d'eau il y a : 1000 / masse molaire de l'eau = 1000/18 = 55,5 mol d'eau

Ds= 60*55,5 = 3,33 kJ K-1kg-1 ; QAB= TA Ds=534* 3,33 =1780 kJ kg-1 ;

or Dh=hsortie-hentrée= W+Q d'où : WAB=1694-1780 = -86 kJ kg-1.

détente isentropique B--> C : Dh= 2075-3018 = - 943 kJ kg-1 ; Ds= 0 d'où QBC=0 et WBC=Dh=- 943 kJ kg-1 .

condensation totale C--> M à pression constante :

Dh= 235-2075 = -1840 kJ kg-1 ; Ds= 24-120 = -106 J K-1 mol-1

Ds= -106*55,5 = -5,89 kJ K-1kg-1 ; QCM= TC Ds=-320* 5,89 =-1885 kJ kg-1 ;

or Dh=hsortie-hentrée= W+Q d'où : WCM=-1840+1885 = 45 kJ kg-1.

compression isentropique M--> D du liquide : Dh= 239-235 = 4 kJ kg-1 ; Ds= 0 d'où QMD=0 et WMD=Dh= 4 kJ kg-1 .

échauffement D-->A à pression constante : Dh= 1324-239 = 1085 kJ kg-1 ;WDA voisin de zéro, fluide quasiment incompressible et P= constante.

or Dh=hsortie-hentrée= W+Q d'où : QDA=1085 kJ kg-1 .

énergie thermique QDB reçue par 1,00 kg de vapeur d'eau, au cours du transfert thermique avec la source chaude :

QDB = QDA +QAB =  1085+1780 = 2865 kJ kg-1.

travail reçu WBC dans la turbine calorifugée : - 943 kJ kg-1 . 

travail reçu WMD à la pompe calorifugée : 4 kJ kg-1  

énergie thermique Qf reçue par 1,00 kg d'eau lors du transfert thermique avec la source froide : -1885 kJ kg-1

rendement h de ce cycle moteur : travail disponible / énergie reçue de la source chaude

|somme des travaux | :|-86-943+4|= 1025 kJ kg-1

énergie reçue de la source chaude 1780+1085 = 2865 kJ kg-1 ; rendement h = 1025/2865*100 = 36%.

production et utilisation des RX pour l'étude d'un cristal

Un tube de Coolidge est schématisé ci-dessous :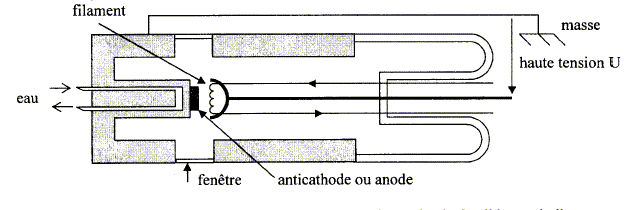

  1. Rappeler le fonctionnement d'un tube de Coolidge en indiquant le rôle du filament, de la haute tension et de l'anticathode.
    - Expliquer qualitativement en quoi le rendement énergétique proche de 1% de cet émetteur de rayonnement impose un refroidissement par eau.
  2. Spectre du rayonnement à la sortie du tube : le spectre d'émission est formé d'un fond continu sur lequel se superposent des raies d'émission intenses.

    - Etude du fond continu : on admet que certains électrons sont arrêtés brutalement dans l'anticathode. Exprimer leur énergie cinétique E à l'arrivée sur l'anticathode en fonction de la haute tension U.
    - En admettant que cette énergie est intégralement convertie en énergie de rayonnement X, montrer que la longueur d'onde X alors émise est donnée par : l0=k/U. On exprimera k en fonction de h, c et e et on calculera sa valeur.
    e= 1,60 10-19 C ; h= 6,63 10-34 J s ; c= 3,00 108 m/s
    - Indiquer à quoi correspond l0 sur le spectre d'émission. Préciser si cette caractéristique dépend du matériau de l'anticathode ; justifier.

  3. Etude du spectre de raies : à l'aide d'un diagramme énergétique représentant les niveaux d'énergie K, L, M d'un atome de l'anticathode, expliquer le processus physique en deux étapes qui génère les raies d'émission.
    - Ces raies sont-elles caractéristiques du matériau de l'anticathode ? Justifier.
    - On fournit les valeurs des longueurs d'onde de raies X émises par un atome de cobalt : lKa=0,179 nm ; lKb=0,162 nm ainsi que l'énergie de liaison (eV) d'un électron situé sur la couche indiquée de l'atome de cobalt : couche K : 7,71 103 ; L : 765 ; M : 36,4. Justifier les valeurs des longueurs d'onde données ci-dessus à partir des énergies de liaisons de l'atome de cobalt.
  4. Analyse cristallographique : on envoie un faisceau parallèle du rayonnement précédent de longueur d'onde l= 0,179 nm sur un cristal dont le réseau est cubique simple. On relève sur la figure de diffraction une raie d'ordre n=1 pour un angle de 15,5°. Cette raie correspond à la famille des plans réticulaires parallèles aux faces des mailles cubiques.

    - Montrer que la loi de Bragg s'écrit dans ce cas : 2d sin q= nl.
    - Calculer le paramètre de la maille a.

corrigé
Tube de Coolidge : tube dans lequel règne un vide poussé (environ 10-4 Pa).

Les électrons sont émis par un filament de tungstène chauffé par un courant électrique (effet Joule). Le filament joue le rôle de cathode. On établit entre la cathode et l'anode une tension élevée ; celle-ci accélère les électrons émis par le filament. Les électrons accélérés frappent l'anode.

La plus grande partie de la puissance électrique (99 %) est dissipée sous forme de chaleur dans l'anode. Les tubes sont refroidits par une circulation d'eau.

énergie cinétique E à l'arrivée des électrons sur l'anticathode en fonction de la haute tension U:

La vitesse initiale des électrons est négligeable ; le poids des électrons est négligeable devant la force électrique.

La seule force qui travaille est la force électrique : son travail est moteur et vaut W= eU ( e : charge élémentaire)

Le théorème de l'énergie cinétique s'écrit : Ec finale - Ec départ= ½mv² 0= eU.

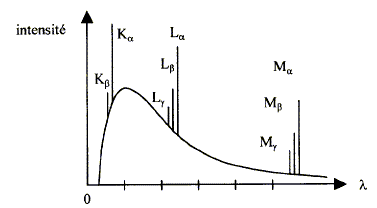
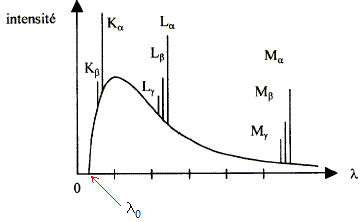
énergie du rayonnement X : E= hc/l0 = eU d'où l0 = hc/(eU) = k/U avec k = hc/e
k =6,63 10-34 * 3,00 108 / 1,60 10-19 =1,24 10-6 V m

En bombardant un solide à l'aide un faisceau d'électrons, on observe un freinage et une déviation des électrons dûs champ électrique des noyaux de la cible.

Or une charge électrique dont la vitesse varie rayonne d'après les équations de Maxwel. Le freinage des électrons n'est pas quantifiée : les énergies des photons ne sont pas quantifiées ; le spectre en énergie est continu.

L'énergie maximale des photons X est égale à l'énergie cinétique initiale eU des électrons. Le spectre intensité = f( longueur d'onde) commence à partir de la valeur l0. Or l0 = hc/(eU) ; l0 ne dépend que de la tension accélératrice et en aucun cas de la nature de la cible.

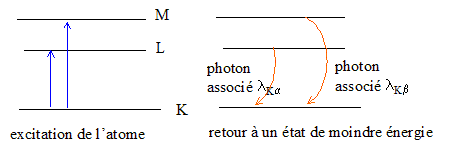
l'énergie de l'atome est quantifiée : le spectre de raies est caractéristique des atomes constituant de l'anticathode.

l'énergie du phoiton X émis est égale à la différence d'énergie entre deux niveau de l'atome : E= kc/l soit l = hc/E

transition L--> K : énergie du photon = 7710-765=6945 eV soit 6945*1,6 10-19 = 1,111 10-15 J. 

lKa=hc/E = 6,63 10-34*3 108 / 1,111 10-15= 0,179 nm

transition M--> K : énergie du photon = 7710-36,4=7673,6 eV soit 7673,6*1,6 10-19 = 1,228 10-15 J. 

lKb=hc/E = 6,63 10-34*3 108 / 1,628 10-15= 0,162 nm  

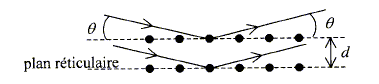
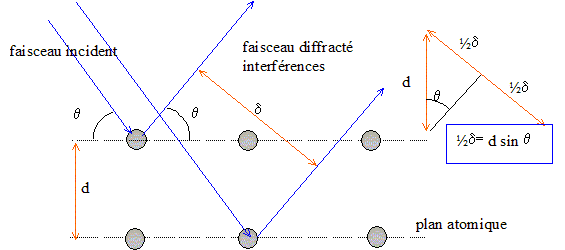
 Chaque fois que la différence de marche d est égale à un multiple de la longueur d'onde, on observe une interférence constructive.

la loi de Bragg s'écrit : d = nl = 2 d sin q

n=1 ; q=  15,5 ° ; l= 0,179 10-9 m ; d= l/(2sin q) = 0,179 10-9 / (2 sin 15,5) = 3,35 10-10 m= 0,335 nm.

le paramètre de la maille cubique simple est égale à d.
retour -menu