|
|
||||
|
||||
|
|
Données : masse volumique de l'eau m= 1,0 103 kg m-3 ; pression atmosphérique P0 = 1,0 105 Pa.
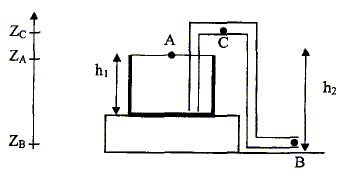
corrigé Application du théorème de Bernoulli entre A et B : PA + rgzA + ½rv²A = PB + rgzB + ½rv²B. d'une part PA= PB = pression atmosphérique d'autre part la vitesse en A est négligeable de vant la vitesse en B d'où : rgzA = rgzB + ½rv²B ; g(zA-zB)=½v²B ; v²B= 2g(zA-zB) ; vB= [2g(zB-zA)]½ = [20*1,5]½ = 5,5 m/s. Le point B doit être plus bas que l'altitude du fond de la piscine pour que celle-ci se vide entièrement. : Dans l'hypothèse où B est à la même altitude que le fond de la piscine : en fin de vidange zA-zB est proche de zéro et en conséquence vB fin est quasiment nulle ; il restera donc un peu d'eau au fond de la piscine.
Débit volumique Q de l'écoulement de l'eau à la sortie du tuyau pour cette vitesse : Q ( m3/s) = section du tuyau (m2) * vitesse (m/s) section : S= pr² = 3,14 10-4 m² Q= 3,14 10-4 * 5,5 = 1,7 10-3 m3/s. Au cours de la vidange le débit volumique diminue car la vitesse vB diminue. Le débit volumique en C est égal au débit volumique en B : de plus les sections du tuyau en B et en C sont identiques : donc les vitesses d'écoulement en B et en C sont identiques. Expression de la pression au point C : Application du théorème de Bernoulli entre B et C : PC + rgzC + ½rv²C = PB + rgzB + ½rv²B. Or vB=vC d'où : PC + rgzC = PB + rgzB ; PC = PB + rg( zB-zC).
il faut que la pression au point C soit supérieure à 0 : PB + rg( zB-zC) =0 zC-zB = PB /( rg ) =105 / (10 * 103 )= 10 m. En plaçant le point C suffisamment haut, le tuyau constitue un bon siphon ; dès qu'il est amorcé, on est sûr de vider la piscine.
|
|||
|
Un manège est un solide en rotation autour d'un axe vertical D. Son moment d'inertie vaut I=2,0 104 kg m². Le manège tournant à la vitesse de 10 tours / minute, l'exploitant le freine et le manège s'arrête après avoir effectué 2 tours.
corrigé vitesse de rotation w en rad/s du manège avant freinage : fréquence : f= 10 / 60 = 1/6 tour/seconde w = 2pf = 2*3,14/6 = 1,0 rad/s. ( 1,047 rad/s) moment supposé constant, des forces de freinage : ½Iw²fin - ½Iw²début = Mq avec q = 2*2p radians ( arrêt en deux tours) - ½Iw²début = M 4p ; M= - ½Iw²début / (4p) M= -0,5 *2 104*1,0472 / (4*3,14) = -8,7 102 Nm.
|
||||
|
Sur un banc à coussin d'air, un objet S, de masse m=20 g est relié à un ressort horizontal de raideur k = 0,33 N/m et de masse négligeable. A vide le ressort a une longueur l0= 10 cm. On néglige les frottements. On repère la position de S par l'abscisse x. L'origine correspond à la longueur à vide du ressort. 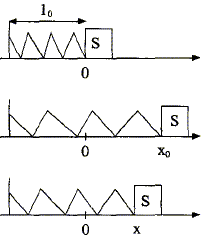
corrigé 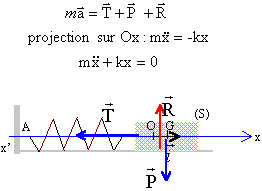 avec w0² = k/m avec w0² = k/m
Les conditions initiales sont : x0 = + 4,0 cm. A t=0 on lâche le ressort sans vitesse initiale. Les solutions de l'équation différentielle sont de la forme x(t) = A cos ([k/m]½t + B) x(0 ) =x0 = Acos B d'où cos B=1 soit B=0 et A = x0
; x(t) = x0 cos ([k/m]½t) w0² = k/m = 0,33 / 0,02 = 16,5 ; w0 = 4,06 rad/s T= 2p/ w0 =6,28 / 4,06 = 1,5 s. Dans les conditions de l'expérience, on considère que
l'énergie mécanique se conserve. Em=Ep+Ec
= constante. Cette énergie est-elle minimale ( Ep =0) pour x=0, ressort non déformé. Expression de l'énergie cinétique Ec de S en fonction de m et v : Ec = ½mv² = Em-Ep = Em-½kx². L'énergie cinétique est maximale au passage à la position d'équilibre x=0 ; L'énergie cinétique est nulle lorsque x= +x0 et lorsque x= -x0, l'énergie mécanique est alors sous forme potentielle.
|
||||
|
|