Aurélie 15/06/06

Produire un son ( bac Réunion 2006)



Google



 Description du montage :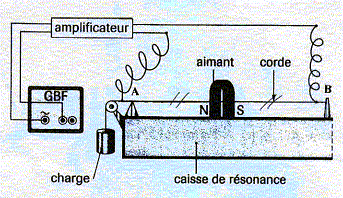

Le courant sinusoïdal traversant la corde permet de générer des ondes transversales. Pour des fréquences bien déterminées, des ondes stationnaires apparaissent entre les points A et B. On observe alors un ou plusieurs fuseaux de vibration. Ce montage permet d'étudier les différents paramètres qui influent sur les ondes stationnaires.

Pour la corde utilisée on a obtenu un fuseau de vibration pour la fréquence f= 40 Hz.

  1. Comment appelle-t-on le mode de vibration correspondant à cette fréquence ?
  2. Comment appellet-on les autres modes de vibrations de la corde ? Quelles sont les valeurs des fréquences qui permettent de les obtenir ?
  3. Quelle est la relation liant la célérité c, la fréquence f, la longueur d'onde l de l'onde apparaissant sur la corde ?
  4. L'onde est stationaire lorsque la distance parcourue par l'onde lors d'un aller et retour est égal à un multiple de la longueur d'onde. Quelle est la relation liant la longueur L de la corde et la longueur d'onde ? Etablir la relation liant c, L et f.
  5. Quelle fréquance doit avoir le courant sinusoïdal pour obtenir deux fuseaux de vibrations ? Où est-il judicieux de placer l'aimant dans ce cas ?

Vibration d'une corde de guitare :

Les différents modes de vibration d'une corde vérifient la relation : f = k/(2L) [F/m]½ ;

k : nombre entier ; L : longueur de la corde (m) ; F :tension mécanique en N ; m : masse linéique en kg m-1 ; f : fréquence (Hz).

Une guitare présente six cordes de masses linéique différente. Cahque corde est reliée à une clé permettant de régler sa tension. La longueur d'une corde est L= 65 cm. L'une des cordes, dite " corde n°2" est la corde du La1 de fréquence 110 Hz.

  1. Quel est l'intérêt de pouvoir régler la tension des cordes ?
  2. Pourquoi les cordes on-elles des masses linéiques différentes ?
  3. Un musicien veut accorder la corde n°2. Avant l'accord il pince cette corde. On enregistre à l'aide d'un micro le son émis par cette corde. On obtient l'enregistrement ci-dessous :
  4. Quelle est la fréquence de la note émise ?
  5. Un logiciel permet de faire l'analyse spectrale de l'enregistrement précédent. Lequel des deux spectres ci-dessous correspond à l'enregistrement ? Justifier
  6. Comment le musicien doi-il agir sur la corde pour obtenir le La1 ? 

corrigé

Onde stationnaire le long d'une corde :

On observe un seul fuseau pour la fréquence f= 40 Hz : il s'agit du mode propre dit " fondamental" ( n=1)
Les autres modes propres de vibration de la corde de longueur L s'appellent " harmoniques " ( n>1)

Les fréquences des harmoniques sont des multiples de la fréquence du mode fondamental :

80 Hz ; 120 Hz ; 160 Hz; 200 Hz ....

relation entre célérité c (m/s), fréquence f (Hz) et longueur d'onde l (m) : l = c / f

relation entre la longueur de la corde et l :

"l'onde est stationaire lorsque la distance parcourue par l'onde lors d'un aller et retour est égal à un multiple de la longueur d'onde"

d'où 2L=nl avec n entier soit L= nl/2

relation liant c, L et f : L= nl/2 et l = c / f d'où L= nc/(2f).

fréquence du courant pour avoir deux fuseaux : 2*40 = 80 Hz

il faut placer l'aimant sous un ventre de vibration ( surtout pas sous un noeud)


vibration d'une corde de guitare :

intérêt de pouvoir modifier la tension des cordes :

fréquence f = k/(2L) [F/m]½ ; en modifiant la tension d'une corde, on modifie la fréquence du son émis par la guitare, ce qui permet d'accorder la guitare.

Les cordes ont des masses linéiques différentes :

la fréquence du son émis par l'instrument est d'autant plus grave (fréquence faible) que la masse linéique de la corde est plus grande.

chaque corde corespond à une note de musique différente de la note émise par la corde voisine.

accorder une corde :

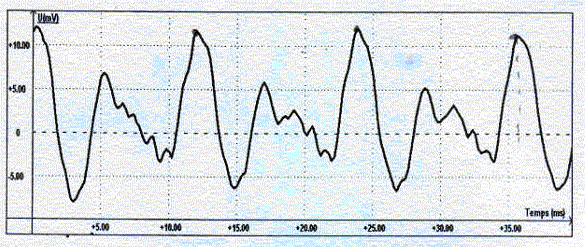
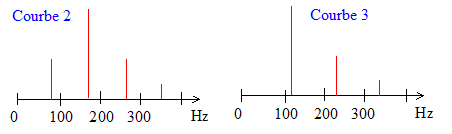
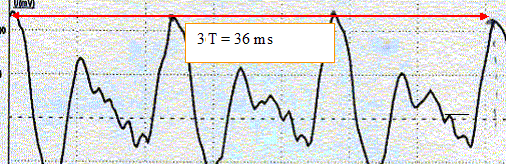
fréquence de la note émise :

période T= 12 ms = 12 10-3 s ; f=1/T = 1000/12 = 83 Hz

la courbe 3 ne convient pas : les fréquences correspondants aux pics sont des multiples de 110 Hz

la courbe 2 convient : les fréquences correspondants aux pics sont des multiples de 83 Hz

Pour accorder cette corde sur la fréquence du La1 ( 110 Hz), le musicien doit augmenter la tension de celle-ci afin que la fréquence actuelle 83 Hz augmente jusqu'à la valeur 110 Hz.

retour -menu