mouvement rectiligne uniformément varié

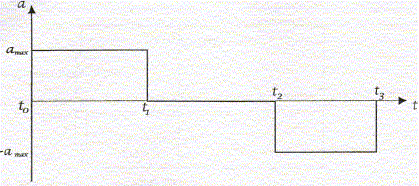
Une grue portuaire soulève verticalement une charge de masse M = 10 tonnes, par l'intermédiaire d'un câble de masse négligeable, en un lieu où l'accélération de la pesanteur g = 9,81 m.s^-2. Cette dernière est initialement au repos à une hauteur h =0 m. Le chronogramme qui suit représente 1'évolution de l'accélération. À l'instant t₃, la charge est de nouveau immobile.

Au temps t_l = 3,5 s, la charge a atteint une hauteur h =6 m. t₂=6 s

La vitesse initiale est nulle ; l'altitude initiale est nulle. L' accélération a_max prise par la charge est telle que :

h=½a_maxt₁² soit a_max = 2h / t₁² = 12 / 3,5² = 0,98 m/s²

valeur de la tension T_l du câble pendant cette phase de l'ascension :

La charge est soumise à son poids ( vertical, vers le bas, valeur mg ) et à la tension T₁ du câble, verticale vers le haut. Ecrire la seconde loi de Newton sur un axe vertical ascendant -mg + T₁ = ma_max soit T₁ = m( g+a_max ) = 10⁴ *(9,81+0,98) = 1,08 10⁵ N.

Dans la seconde phase du mouvement, ( mouvement rectiligne uniforme) l'accélération est nulle. T₂=mg = 9,81 10⁴ N.

vitesses V₁ et V₂ atteintes au temps t₁ et t₂ :

V₁= a_max t₁ = 0,98*3,5 = 3,43 m/s.

entre t₁ et t₂ le mouvement est rectiligne uniforme : V₁ = V₂

Calcul du temps t₃ : entre t₂ et t₃ l'accélération est négative (-0,98 m/s²) : la vitesse diminue puis s'annule à la date t₃.

v₃(t) = -a_max (t-t₂) + v₂ = -0,98 (t-6) + 3,43 ;

à la date t₃ , la vitesse s'annule : d'où : -0,98 (t₃-6) + 3,43=0 soit t₃-6 = 3,43/0,98 = 3,5 ; t₃= 9,5 s.

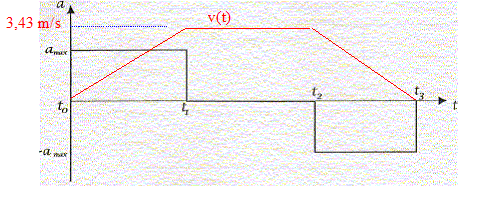
allure de la vitesse en fonction du temps entre les temps t₀ et t₃.

Le câble risque de se rompre s'il est soumis à une tension supérieure à T_max= 4 l0⁵ N. La grue soulève désormais une charge d'une masse M' = 15 tonnes, initialement au repos d'une hauteur h' = 10 m d'un mouvement vertical uniformément accéléré.

durée minimale t' de l'ascension pour éviter la rupture du câble : T_max= 4 l0⁵ N ; P= M'g = 1,5 10⁴*9,81 =1,47 l0⁵ N

la seconde loi de Newton s'écrit sur un axe vertical ascendant : T_max-P= M'a d'où a = (T_max-P)/M' =2,53 10⁵ / 1,5 10⁴ = 16,867 m/s²

h' = ½a t'² soit t'² = 2h'/a = 20 / 16,867 = 1,186 soit t' = 1,09 s.