|
d'après bac S Maroc 2006 |
||||
|
||||
|
|
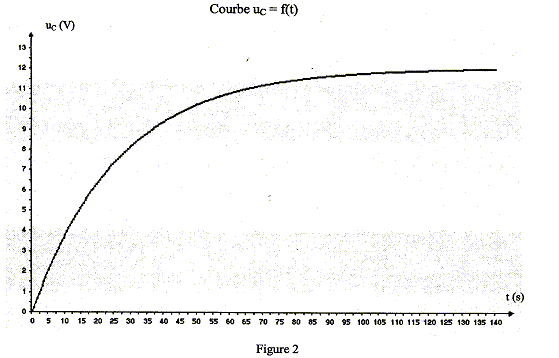
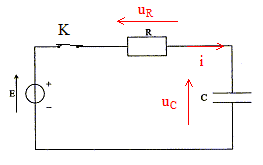
Etude théorique d'un dipole RC soumis à un échelon de tension : Le montage du circuit électrique schématisé ci-contre (figure 1) comporte : - un générateur idéal de tension de force électromotrice E = 12,0 V ; - un conducteur ohmique de résistance R inconnue ;- un condensateur de capacité C = 120 µF ;- un interrupteur K. Le condensateur est initialement déchargé. À la date t = 0, on ferme l'interrupteur K. 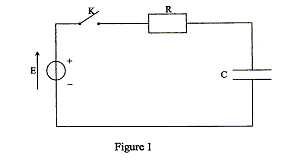 Par ailleurs, on note q la charge de l'armature du condensateur qui se chargera positivement.
Application : Au dipôle RC précédemment étudié, on associe un montage électronique qui commande l'allumage d'une lampe : la lampe s'allume lorsque la tension uc aux bornes du condensateur est inférieure à une valeur limite ual =6,0V; la lampe s'éteint dès que la tension uc aux bornes du condensateur est supérieure à cette valeur limite ua1= 6,0 V. Le circuit obtenu (figure 3) est le suivant : 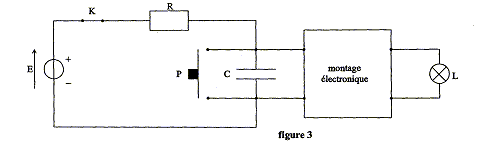 Fonctionnement du bouton poussoir : Lorsqu'on appuie sur le bouton poussoir, ce dernier entre en contact avec les deux bornes du condensateur et se comporte comme un fil conducteur de résistance nulle. Il provoque la décharge instantanée du condensateur. Lorsqu'on relâche le bouton poussoir, ce dernier se comporte alors comme un interrupteur ouvert.
Etude théorique d'un dipole RC soumis à un échelon de tension :
expression de UR en fonction de i : uR= Ri expression de i en fonction de la charge q du condensateur : i = dq/dt ( q charge de l'armature supérieure du condensateur) relation liant q et uc : q= Cuc. expression de i en fonction de la capacité C et de la tension uc : i = Cduc/dt loi d'additivité des tensions : E= uR + uc. équation différentielle notée (1) à laquelle obéit uc : E= RCduc/dt + uc. uc = E (1- exp(-t/t)) est solution de l'équation différentielle ; dériver par rapport au temps : duc/dt = E/(RC)exp(-t/t) repport dans (1) : E= Eexp(-t/t) + E (1- exp(-t/t)), vérifiée quel que soit le temps, donc uc = E (1- exp(-t/t)), avec t = RC, est solution de l'équation différentielle vérification de la condition initiale : à t = 0 le condensateur n'est pas chargé et uc(0) = 0. uc (0)= E (1- exp(-0/t)) = E(1-1) = 0 la fonction uc = E (1- exp(-t/t)) vérifie bien la condition initiale. analyse dimensionnelle du produit t = RC : R : résistance soit tension / intensité C : capacité soit charge / tension et une charge est une intensité fois un temps d'où C : intensité * temps / tension par suite RC a la dimension d'un temps et t
est bien homogène à une durée.
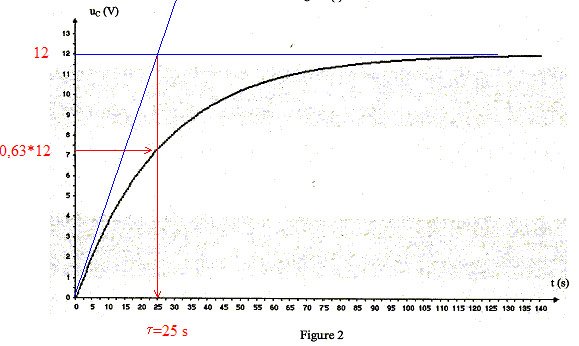
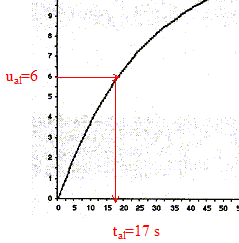
Application : Le condensateur est initialement chargé avec une tension égale à 12 V, la lampe est éteinte. On appuie sur le bouton poussoir P : on provoque la décharge instantanée du condensateur et uc s'annule. Or la lampe s'allume lorsque la tension uc aux bornes du condensateur est inférieure à une valeur limite ual =6,0V : donc la lampe s'allume. Lorsqu'on relâche le bouton poussoir, ce dernier se comporte alors comme un interrupteur ouvert. Le condensateur relié au générateur de tension E, se charge ; la tension uc à ses bornes augmente jusqu'à atteindre la valeur E=12 V. La constante de temps du dipôle RC utilisé est t = 25 s. Le condensateur se charge très lentement ( 5 t = 125 s). La lampe reste allumée tant que la tension aux bornes du condensateur reste inférieure à ua1= 6,0 V, puis la lampe s'éteint. expression littérale de la date tal, à laquelle la tension aux bornes du condensateur atteint la valeur limite ual en fonction de ual, E et t : ual = E (1- exp(-tal/t)) ; ual / E =1- exp(-tal/t) ; 1-ual / E = exp(-tal/t) ln(1-ual / E )= -tal/t ; tal = -t ln(1-ual / E ) tal = -25 ln(1-6/12) = -25 ln 0,5 = 17 s. Détermination graphique de la valeur de tal
à l'aide de la courbe uc = f(t) : La tension aux bornes du générateur E étant constante, pour augmenter la durée d'allumage tal = -t ln(1-ual / E ), il faut augmenter t : donc augmenter la résistance R ou/et augmenter la capacité C du condensateur.
|
|||
| |
||||
|
|