|
La Logan au banc d'essai, d'après bac S Liban 2006 |
||||
|
||||
|
|
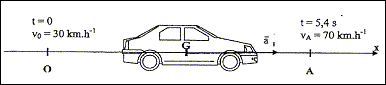
La Dacia Logan, conçue par le constructeur français Renault est produite au départ en Roumanie. Elle a fait la une de l'actualité lors de son lancement commercial : elle était en effet présentée comme " la voiture à 5000 euros ". Même si son prix fut finalement plus élevé que prévu, les journalistes automobiles étaient impatients d'évaluer cette voiture d'un nouveau genre. L'exercice propose de détailler certains tests routiers effectués par les essayeurs d'un magazine automobile et d'étudier un composant du système d'alimentation en gazole du moteur Diesel qui peut équiper la Logan. Donnée : Accélération de la pesanteur: g = 9,8 m.s-2. Les parties A et B sont indépendantes. Partie A: Performances et comportement routier Les paragraphes I, II et III sont indépendants. I - Mesures de reprises Le test consiste à faire passer la voiture, en pleine accélération et sur le deuxième rapport de la boîte de vitesses, de 30 km.h-1 à 70 km.h-1 sur une portion de circuit rectiligne et horizontale. On mesure alors le temps nécessaire à cette accélération, ce qui donne une bonne indication de la capacité du véhicule à s'insérer et à évoluer dans le trafic routier. Résultat du test d'accélération donné par le magazine: "passage de 30 km.h-1 à 70 km.h-1 en 5,4 s ".
II - Virage sur une trajectoire circulaire Un second test consiste à faire décrire à la voiture une trajectoire circulaire de rayon R = 50 m. Ce test donne une bonne indication de la tenue de route du véhicule. Une chronophotographie (en vue de dessus) représentant les positions successives du centre d'inertie G de la Logan pendant ce test est donnée en annexe à rendre avec la copie (Figure 1 ). La durée t = 1,00 s sépare deux positions successives du centre de masse G. 
III - Suspension La Logan est constituée d'une caisse métallique reposant sur ses roues par l'intermédiaire d'une suspension, formée d'un ensemble de quatre ressorts avec amortisseurs. On peut modéliser cette voiture par un pendule élastique vertical dont les oscillations sont amorties. La seule particularité de ce pendule est d'avoir la masse M (correspondant à la caisse) à l'extrémité supérieure du ressort de raideur k ; la mise en oscillation ayant lieu lorsque l'extrémité inférieure du ressort (correspondant à la roue) subit un déplacement vertical, par exemple lors d'un passage sur une bosse (dos d'âne). 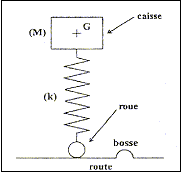
Partie B : " L'injecteur par rampe commune " Malgré les tarifs modérés de la Logan, son moteur Diesel bénéficie d'une technologie de pointe: le système d'injection directe de gazole par rampe commune. L'élément essentiel est l'injecteur qui pulvérise en quelques fractions de seconde une très faible quantité de gazole directement dans la chambre de combustion où se produit l'explosion du mélange air-gazole. On peut schématiser cet injecteur par un long tube creux, percé à son extrémité inférieure d'un très petit trou bouché par une aiguille. C'est par ce trou que pourra sortir le gazole lorsque l'aiguille sera déplacée vers le haut. Pour déplacer cette aiguille métallique vers le haut, on utilise une bobine qui, lorsqu'elle est traversée par un courant électrique, se comporte comme un aimant et attire alors l'aiguille à elle. Dès que le courant est coupé, l'aiguille reprend sa position initiale et bouche à nouveau le trou. Un laboratoire de recherche d'un constructeur concurrent demande à un technicien d'étudier les caractéristiques de cette bobine. I - Prévision d'un dipôle bobine-conducteur ohmique : Pour préparer un protocole d'étude de la bobine de l'injecteur, le technicien choisit d'abord une bobine, d'inductance L et de résistance interne r connues. 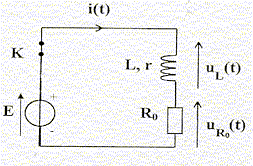 Il réalise ensuite le circuit ci-contre où l'interrupteur est au départ fermé. On rappelle que la tension aux bornes de la bobine est: uL(t) = L.di/dt + r.i Données : E = 6,0 V; L = 0,94 H ; R0 =150 W; r = 20 W.
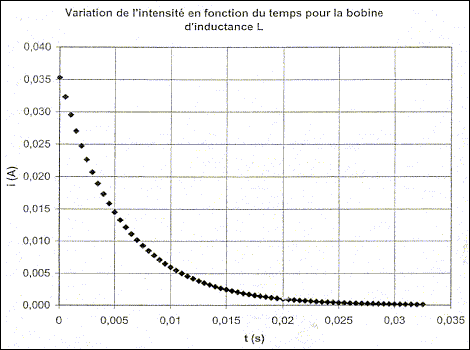
II - Mesure des caractéristiques de la bobine de l'injecteur Le technicien utilise maintenant la bobine de l'injecteur afin de déterminer son inductance L' et sa résistance r' . Il réalise avec cette bobine le circuit de l'étude précédente (E = 6,0 V; R0= 150 W) et il effectue une nouvelle acquisition comme à la question I-3. A l'instant t0 = 0, il ouvre l'interrupteur et obtient le tracé donné sur la Figure 3 en annexe à rendre avec la copie. 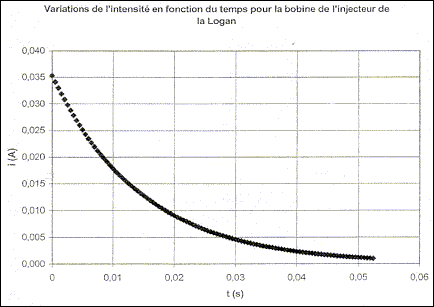
relation entre le vecteur accélération et le vecteur vitesse du centre d'inertie G du véhicule : Le vecteur vitesse est une primitive du vecteur accélération ; l'accélération étant constante, sur l'axe Ox, v = a1t+v0. Exprimer les vitesse en m/s : 30/3,6 = 8,33 m/s ; 70/3,6 = 19,44 m/s a1 = (v-v0) / t =(19,44-8,33)/5,4 =2,1 m/s². équation horaire de la position x(t) du centre d'inertie G : La position est une primitive de la vitesse : x(t) = ½a1t² + v0t = 1,05t²+8,33 t. distance D parcourue : D= 1,05*5,4²+8,33*5,4 = 75,6 ( 76 m) normes des vitesses v3 et v5 du centre d'inertie G v3=G2G4/(2t) ; v5=G4G6/(2t) G2G4 voisin G4G6 voisin 2 cm soit en tenant compte de l'échelle : 20 m v3= v5= 20/2 = 10 m/s soit 10*3,6 = 36 km/h Représentations des vecteurs vitesses v3 et v5 : tangents à la trajectoire aux points considérés, sens du mouvement expression du vecteur accélération a4 au
point G4 : valeur de a4=Dv4/(2t) avec Dv4 voisin 5 m/s ( d'après le graphe) a4= 5/2 = 2,5 m/s² accélération de " latérale " : accélération centripète la valeur de cette accélération n'est pas négligeable et représente 0,25 g ; les passagers en ressentiront les effets. inventaire des forces qui s'exercent sur la caisse : poids, verticale, vers le bas, valeur Mg ; tension du ressort, verticale vers le haut, valeur k|D l0| relation entre |D l0|, M, k et g en appliquant le principe d'inertie le poids et la tension se neutralisent : ces forces ont la même valeur k|D l0| =Mg établir la relation k = mg/h . k(|D l0|+h)=(M+m)g k(|D l0|+h)=(M+m)g k(|D l0| + kh = Mg+mg ; kh=mg dimension de k : masse ; g accélération soit longueur / temps² ; h : longueur mg/h : masse /temps² ( MT-2) valeur de k : mg/h = 280*9,8/0,03 = 9,1 104 kg s-2. période propre des oscillations : T0=2p(m/k)½=6,28((1095+70)/ 9,1 104)½=0,71 s. nom du régime oscillatoire observé : apériodique si l'amortissement est moins important, le régime devient pseudopériodique. phénomène observé par l'essayeur : résonance période des excitations pour que ce phénomène ait lieu : 0,71 s ( période propre de l'oscillateur ) distance D nécessaire pour que le phénomène ait lieu à une vitesse v = 80 km.h-1 : ( 80/3,6 = 22,22 m/s) D= v Dt = 80/3,6*0,71 = 15,8 ( 16 m) autre moyen d'éviter le phénomène ressenti lors du passage sur le ralentisseur : en augmentant la vitesse, la période de l'excitateur n'est plus égale à la période propre de l'oscillateur ( le phénomène de résonance s'atténue ou disparaît) En régime permanent l'intensité est constante et dI0/dt est nulle ; la tension aux bornes de la bobine est uL=rI0 Additivité des tensions : E= R0I0+rI0 soit I0=E/(R0+r) Equation différentielle vérifiée par l'intensité i(t) : uL(t) + uR0 (t) = 0 Ldi/dt+ri + R0i=0 ; Ldi/dt + (R0+r) i=0 dimension de t : E=½Li² soit L=2E/i² : énergie / intensité au carré Energie dissipée dans un résistor : E= Ri²t soit R = E/(i²t) : énergie / ( intensité² * temps) d'où L/((R0+r) a la dimension d'un temps valeur de t : L/((R0+r) =0,94 / 170=5,5 10-3 s= 5,5 ms. l'intensité i(t) pour t = t : lire l'ordonnée correspondante à l'abscisse t= 5,5 ms ; d'où i=0,013 A résistance interne r' de la bobine : R0+r'=E/I'0=6/0,035 = 171 W soit r' = 21 W. Évaluation graphique de la constante de temps t': t' voisin 0,012 s inductance L' de la bobine : L' = (R0+r') t '= 171*0,012 = 2,1 H
|
|||
| |
||||
| |
||||
|
|