|
Un acide rencontre une base, analogies électromécaniques , fusion deutérium tritium |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
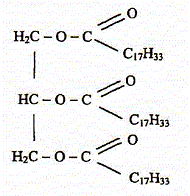
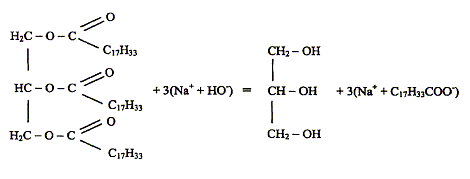
Une expérience instructive, très simple à réaliser, consiste à disposer du bicarbonate de soude au fond d'une flûte à champagne, puis à y ajouter délicatement de l'huile végétale claire et, au-dessus, du vinaigre (voir ci-dessous) : […] le vinaigre pénètre dans l'huile en formant des gouttelettes qui descendent au fond du verre. Puis, à peine touchent-elles le fond qu'elles remontent jusqu'à la surface, avant de redescendre à nouveau ...II faut attendre cinq bonnes minutes avant que cette danse ne s'arrête !... " "…Au bout du voyage, les gouttes entrent en contact avec le bicarbonate de soude. Cela provoque une réaction chimique qui conduit à une émission de dioxyde de carbone. Rapidement, le gaz ainsi créé s'agrège en bulles qui s'accrochent sur les gouttelettes de vinaigre. Le volume de ces bulles augmente jusqu'à ce qu'elles remontent, entraînant avec elles les gouttelettes. Une fois arrivées à la surface, les bulles éclatent. Résultat : débarrassées des bulles les petites gouttes de vinaigre redescendent dans l'huile. Et le manège recommence, jusqu'à disparition du vinaigre. D'après Alain Schuhl dans Science et Vie Junior N°165 juin 2003 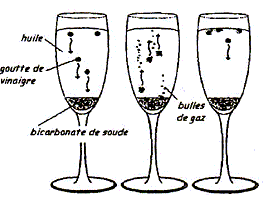 L'étude de la transformation chimique entre le bicarbonate de soude et le vinaigre fait l'objet cet exercice. Les parties 1, 2 et 3 sont Indépendantes. I Etude de l'huile : L'acide oléique a pour formule semi-développée H3C-(CH2)7-CH = CH-(CH2)7- OOH ; on le notera simplement C17H33COOH. On considère que l'huile alimentaire, utilisée dans l'expérience est composée uniquement de triester de l'acide oléique et du propan-1,2,3-triol de formule semi-développée HOCH2-CHOH-CH2OH.
II. Etude du vinaigre. Le vinaigre est une solution aqueuse d'acide acétique de formule CH3COOH. On mesure le pH d'une solution diluée. Le pH vaut 3,40 et la concentration de la solution diluée est 1,00.10-2 mol.L-1. Données :- Pour le couple acido-basique CH3COOH / CH3COO- , pKa = 4,75. Valeurs des conductivités molaires ioniques : l(H3O+) = 35,0 .10-3 S.m².mol-1 ; l(CH3COO-) = 4,09 .10-3 S.m².mol-1
III. Données et rappels : - Température absolue T : elle se mesure en kelvins (K) et vaut T = 273 + q, q étant la température exprimée en degrés Celsius (°C). - Loi des gaz parfaits : la pression p, le volume V et la température absolue T d'une quantité de matière n de gaz sont liés par la relation p.v = n.R.T. Dans le système international, la constante R vaut R = 8,31 J.K-1.mol-1. - Couples acido-basiques : On rappelle que le pKa du coupe acide acétique l' ion acétate vaut pKa = 4,75. Celui du couple CO2 ,H2O / HCO3- vaut pKa = 6,35 - On donne les masses molaires : M(NaHCO3) = 84 g.mol-1 et M(CH3COOH) = 60 g.mol-1 On considère la réaction chimique correspondant à la transformation qui a lieu lorsque la gouttelette de vinaigre touche le bicarbonate de soude solide se trouvant au fond du verre. Le " bicarbonate de soude " du commerce est en réalité de l'hydrogénocarbonate de sodium NaHCO3 (s). Le vinaigre est une solution aqueuse d'acide acétique CH3COOH (aq).
corrigé autre nom du propan-1,2,3-triol : glycérol
En milieu très basique (soude concentrée) et à chaud, l'huile subit une hydrolyse basique : saponification les produits obtenus : oléate de sodium ( savon) et glycérol équation modélisant la réaction chimique entre l'acide acétique et l'eau : CH3COOH + H2O=CH3COO- +H3O+. expression littérale de la constante d'équilibre associée à cette réaction : Ka = [CH3COO-][H3O+]/[CH3COOH] = 10-4,75 = 1,78 10-5. Etablir le tableau d'avancement de la réaction. Calculer le taux d'avancement de celle-ci : on raisonne sur 1L de solution
t <<1 , la transformation de l'acide acétique avec l'eau est très limitée Retrouver la valeur de son pH : s = l(H3O+) [H3O+] + l(CH3COO-) [CH3COO-] avec [H3O+] =[CH3COO-] s =( l(H3O+) +l(CH3COO-)) [H3O+] = 15,5.10-3 S.m-1 [H3O+] =s /( l(H3O+) +l(CH3COO-))=15,5.10-3/(35,0 .10-3 +4,09 .10-3 )=0,396 mol m-3 = 3,96 10-4 mol/L pH= -log(3,96 10-4) = 3,40. Ecrire l'équation de la réaction chimique étudiée : CH3COOH + HCO3- = CO2 ,H2O+CH3COO- quantité de matière à l'état initial correspondant à 1,00 g d'hydrogénocarbonate de sodium : m / M = 1/84 = 1,2 10-2 mol.
si HCO3-en défaut, xmax =1,2 10-2 mol. retenir la plus petite valeur : xmax =3,7.10-5 mol. CH3COOH réactif limitant. valeur numérique de l'avancement final xf de cette réaction : la pression est P = 1,02 105 Pa ; la température T= 273+ q =273+ 25 =298 K ; le volume total de gaz dégagé par la réaction V= 0,89 mL =8,9 10-7 m3. xf = PV/(RT) =1,02 105*8,9 10-7 / (8,31*298)=3,7 10-5 mol taux d'avancement final t de cette transformation : xf / xmax =3,7 10-5 /3,7.10-5 = 1 La transformation chimique est donc totale.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
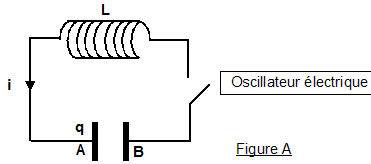
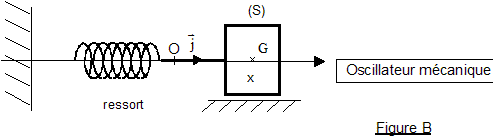
On considère les deux oscillateurs idéaux suivants (voir figures A et B ci-dessus) : un circuit électrique comprenant : - une bobine d'inductance L et de résistance négligeable ; un condensateur de capacité C et d'armatures A et B; un interrupteur. Les conventions d'orientation sont telles que l'intensité du courant est i = dq/dt , q(t) étant la charge instantanée du condensateur, c'est-à-dire celle de l'armature A. Les conditions initiales du fonctionnement sont les suivantes: à t négatif ou nul, l'interrupteur est ouvert et le condensateur porte la charge q(0) = Q0 à t = 0, on ferme l'interrupteur. On donne L= 0,10 H ; C = 10,0 µF et Q0= 10-4 C. ·un système {solide - ressort} horizontal comprenant : - un solide (S), de masse m et de centre d'inertie G, glissant sans frottement dans la direction de l'axe O horizontal et d'origine O (voir Figure B) : si (S) est au repos, G est en O ; à un instant quelconque, G est repéré par son abscisse x - un ressort à spires non jointives de raideur k, de masse négligeable, dont l'une des extrémités est attachée à (S) et l'autre fixée rigidement à un support. Les conditions initiales choisies sont les suivantes: à l'instant t = 0, la position du centre d'inertie du solide vaut X0 et sa vitesse vx est nulle. On donne le rapport m/k=1,0.10-2 S.I. et X0 = + 4,0 cm. I- Oscillateur mécanique On admet que l'équation différentielle vérifiée par x(t) est md²x/dt² +kx=0 où d²x/dt² désigne la dérivée seconde par rapport au temps de la fonction x(t).
II- Oscillateur électrique On admet que l'équation différentielle vérifiée par la charge q(t) est : Ld²q/dt² +q/C=0 On utilise de façon systématique la comparaison entre les deux équations différentielles.
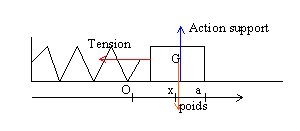
corrigé (S) est soumise à son poids, vertical, vers le bas, valeur mg, à l'action du support, opposée au poids et à la tension du ressort, horizontale, valeur T=kx
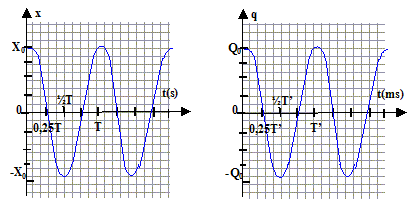
équation différentielle du mouvement : écrire la seconde loi de Newton sur un axe horizontale orienté vers la droite -kx = md²x/dt² ou d²x/dt² + k/m x=0 Je vérifie que x = A.cos(2p t/T+j) est solution de l'équation différentielle : dériver x par rapport au temps : x' = -A2p /Tsin (2p t/T+j) ; x" = -A(2p /T)2 cos (2p t/T+j) = - (2p/T)2 x repport dans l'équation différentielle : - (2p /T)2 x + k/m x=0 doit être vérifiée quelque soit le temps d'où (2p/T)2= k/m soit T² = (2p)2 m/k ou T= 2p(m/k)½. unité du rapport m/k : 2p est sans dimension et T , période exprimée en seconde donc m/k s'exprime en s2. valeur numérique : T= 6,28 ( 10-2)½= 0,63 s. En prenant en compte les conditions initiales du début de l'énoncé : x(0) = X0 . A cos(j) = X0 positif conduit à : A= X0 et j = 0. ou encore sachant que la vitesse initiale est nulle : x'= -A2p /Tsin (2p t/T+j) ; x'(0)= -A2p /Tsin (j) = 0 avec A différent de zéro sin (j) =0 donne j =0 ou j =p ; cette dernière valeur ne peut pas être retenue car A est positif.
l'intensité correspond à la vitesse. En utilisant les similitudes entre les équations différentielles et les conditions initiales x(0) = X0 et q(0)= Q0 : v(t) = x'(t) = -A2p /Tsin (2p t/T) et i(t) = dq/dt conduisent à dq/dt = -A2p /Tsin (2p t/T) par intégration la charge instantanée du condensateur vaut : q(t) = Acos (2p t/T) avec A= charge initiale = Q0 expression de T' en fonction des caractéristiques des composants du circuit : T' = 2p(LC)½. valeur numérique : T' = 6,28 (0,1 10-5)½=6,3 10-3 s. les fonctions x(t) et q(t):
Les oscillateurs réels ne sont pas idéaux : pertes d'énergie ( sous forme de chaleur ) respectivement lors des frottements mécaniques, lors du passage du courant dans les conducteurs électriques (effets joule).
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
La fusion nucléaire, c'est le Diable et le Bon Dieu ! Le Bon Dieu dans les étoiles où elle fait naître tous les atomes, jusqu'à ceux de la vie. Mais le Diable sur Terre où elle fut utilisée à fabriquer des bombes qui pourraient tout anéantir, à commencer par la vie. Mais alors que le diable de la destruction thermonucléaire semble rentrer dans sa boîte, la fusion nucléaire contrôlée dans les réacteurs civils ouvre des perspectives de développement économique durable à très long terme. Paul-Henri Rebut, L'énergie des étoiles - la fusion nucléaire contrôlée. Editions Odile Jacob 1999 (dos de couverture). Notations utilisées: Particules ou noyaux AZX ; Masse de la particule ou du noyau : m( AZX ) ; Energie de liaison du noyau : EL(AZX ).
I- Isotopie
II- Radioactivité
III- Fusion de noyaux
IV- Conditions de la fusion DT La fusion n'a lieu que si les deux noyaux sont en contact.
corrigé isotopes : deux noyaux qui ne diffèrent que par leur nombre de neutrons ; ils ont le même nombre de charge Z le deutérium D dont le noyau contient 1 proton et 1 neutron : 21H ; le tritium T dont le noyau contient 1 proton et 2 neutrons : 31H. D et T sont des isotopes de l'élément chimique hydrogène. noyau radioactif : noyau instable susceptible de conduire par fusion ( pour les plus petits) ou fission ( pour les noyaux lourds) à un ou des noyaux plus stables ; cette réaction nucléaire libère de l'énergie et s'accompagne de l'émission de particules a, b, g. Le tritium T est radioactif b-: équation de la désintégration de T 31H --> 32He + 0-1e Le tritium T a une demie-vie t1/2= 12 ans : au bout de 12 ans la moitié des noyaux initialement présents se sont désintégrés. réaction nucléaire de fusion : deux petits noyaux instables conduisent à un seul noyau stable en libérant de l'énergie. équation nucléaire de la fusion entre un noyau de deutérium et un noyau de tritium, au cours de laquelle se forme un noyau d'hélium 42He: 31H + 21H--> 42He + 10n énergie DE qui peut être libérée par cette réaction en fonction des énergies de masse des particules (ou des noyaux) qui interviennent : DE=Dm c²= [ m(42He)+m(10n)- m(31H) - m(21H)] c² masse m( AZX ) du noyau AZX en fonction de mp, mn, Z, A et de l'énergie de liaison EL(AZX ) : On appelle défaut de masse d'un noyau la différence entre la masse totale des A nucléons séparés ( Z protons et A-Z neutrons ), au repos et la masse du noyau formé, au repos : Dm = m( AZX ) -( Zmp + (A-Z)mn ) m( AZX ) = ( Zmp + (A-Z)mn )+Dm avec Dm <0 on appelle énergie de liaison notée El d'un noyau l'énergie que doit fournir le milieu extérieur pour séparer ce noyau au repos en ses nucléons libres au repos. EL(AZX )= |Dm| c² EL(AZX ) / c² = ( Zmp + (A-Z)mn )-m( AZX ) m( AZX ) = ( Zmp + (A-Z)mn ) -EL(AZX ) / c² Pour la réaction de fusion envisagée, expression de DE en fonction des énergies de liaison : DE = -[EL ( 42He) - EL (T) -EL (D) ]= 28,29-8,481-2,224 = -17,58 MeV. le signe - indique que l'énergie est libérée dans le milieu extérieur. Les noyaux D et T se repoussent : chaque noyau contient des protons positifs ; des charges de mêm signe se repoussent. Quantitativement, la température absolue T (en kelvins) des noyaux est proportionnelle à leur énergie cinétique T= a EC avec "a" constante de proportionnalité. une énergie cinétique de 1 eV correspond une température de 7700 K l'énergie cinétique EC des noyaux, doit être suffisamment importante : EC > 0,35 MeV.( 3,5 105 eV) température minimale des noyaux pour que la fusion ait lieu : 3,5 105 * 7700= 2,7 109 K La température interne du Soleil n'est que de 15 106 K. Dans le soleil, d'autres types de fusion, que celle évoquée ici, doivent ce produire.
|
|||||||||||||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|