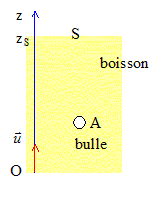
On se propose dans cet exercice de faire une plongée au cœur de l'effervescence d'une boisson gazeuse, d'illustrer et d'interpréter sous l'angle physico-chimique les différentes étapes de la vie éphémère d'une bulle, à savoir : sa naissance, son ascension dans le liquide, et son éclatement en surface. Dans tout l'exercice les bulles seront assimilées à des sphères, et la boisson à un liquide de masse volumique égale à celle de l'eau. Le référentiel d'étude est terrestre considéré comme galiléen.

Masses volumiques : eau r_e = 1,010³ kg.m^-3; dioxyde de carbone r_CO2 = 1,8 kg.m^-3 ; Intensité de la pesanteur: g = 10 m.s^-2.

I- Naissance et décollement d'une bulle :

Dans une bouteille fermée de boisson gazeuse, un équilibre s'établit entre le dioxyde de carbone qui est dissous dans la boisson et le dioxyde de carbone gazeux piégé dans le col de la bouteille. Lors de l'ouverture de celle-ci, l'équilibre est rompu et la boisson se débarrasse d'une partie du dioxyde de carbone dissous qui retourne progressivement en phase gazeuse. Il y a formation de bulles qui vont s'enrichir continûment en gaz au cours de leur remontée.

Dans un verre, les bulles naissent sur des sites de nucléation qui sont des embryons de bulles présents en solution ou de petites poches d'air piégées par des impuretés microscopiques (fibres de cellulose, microcristaux …). La figure 1 illustre cette formation de bulles sur un site de nucléation.

Dès que la valeur de la poussée d'Archimède à laquelle la bulle est soumise dépasse la valeur de la force capillaire qui l'ancre à son site de nucléation, la bulle se détache. Puis une autre bulle naît et subit le même sort.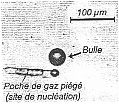

Pour une bulle qui vient de se détacher du site de nucléation dans un liquide de masse volumique r_e :

1. Donner la direction et le sens de la poussée d'Archimède qui s'exerce sur une bulle de volume V₀ dans la boisson.
2. Donner l'expression littérale de sa valeur en fonction du volume V₀ de la bulle.

II- Ascension d'une bulle : à la recherche d'une modélisation satisfaisante.

À l'instant de date t0 = 0 s, une bulle de rayon r0 = 20 mm, située au point A à la profondeur z0 = 0 m dans le repère (O ;z ) (figure 2) se détache de son site de nucléation avec une vitesse initiale v0 nulle dans le référentiel terrestre supposé galiléen. Elle remonte verticalement vers la surface S du liquide, qu'elle atteint avec une vitesse vS d'environ 15 cm.s-1. Dans un premier temps (pour les questions 2.1. et 2.2.), on assimile la bulle de gaz à une sphère dont le volume ne varie pas lors de sa remontée.

1. Étude du mouvement d'une bulle en l'absence de force de frottement :
   - Montrer que le poids P₀ de la bulle a une valeur négligeable devant celle de la poussée d'Archimède F_A en calculant le rapport : P₀ / F_A .
   - En utilisant la deuxième loi de Newton, établir l'expression de la coordonnée a_z du vecteur accélération de la bulle en fonction des masses volumiques r_e et r_CO2 et de g.
   - En déduire l'expression de la valeur de la vitesse de la bulle en fonction du temps.
   - Montrer que la durée t_s théoriquement nécessaire pour que la bulle atteigne la surface avec la vitesse v_s est alors d'environ trente microsecondes.
   - Cette valeur correspond-elle aux observations de la vie quotidienne ? Conclure quant à la validité du modèle proposé.
2. Étude du mouvement de la bulle en présence d'une force de frottement :
   Le liquide exerce sur la bulle une force de frottement, proportionnelle à sa vitesse, de valeur f = k v,, colinéaire et de sens contraire au vecteur vitesse. k est un coefficient qui dépend du rayon de la bulle et de la viscosité du fluide dans lequel elle se déplace.
   - Représenter schématiquement, sans souci d'échelle, les forces non négligeables qui s'exercent sur la bulle en mouvement après son décollement du site de nucléation.
   - En appliquant la deuxième loi de Newton, montrer que l'équation différentielle qui régit l'évolution de la vitesse de la bulle s'écrit alors :
   dv/dt + kv/(r_CO2 v₀) =r_e /r_CO2 g
   - En déduire l'expression littérale de la vitesse limite v_lim atteinte par la bulle.
   - L'application numérique donne v_lim voisin de 1 mm.s^-1. Compte tenu de cette valeur, conclure quant à la validité du modèle proposé.
3. Un autre paramètre à prendre en compte :
   Les modélisations précédentes ne décrivent pas de manière satisfaisante le mouvement de la bulle dans la boisson gazeuse. En particulier, les expériences réalisées dans du champagne montrent que la variation du volume de la bulle ne peut pas être négligée (figure 3). On se propose d'en trouver l'origine.

   On suppose que la quantité de matière n₀ de gaz présent dans la bulle et la température restent constantes. Dans ce cas, lors d'une remontée de 12 cm du point A à la surface S, la diminution de pression du gaz ne ferait augmenter son volume initial que de 2 %. Dans la réalité, l'augmentation du volume est un million de fois supérieure ! Un des deux paramètres supposés constants dans le texte précédent ne l'est donc pas.
   - En s'aidant d'une phrase du texte introductif à la partie 1 de cet exercice, expliquer pourquoi le volume de la bulle augmente si fortement lors de sa remontée.
   - Durant l'ascension le poids de la bulle est toujours négligeable devant la poussée d'Archimède. Sachant que le coefficient k défini à la question 2.2. augmente avec le rayon de la bulle, préciser qualitativement l'influence de la variation du volume de la bulle sur chacune des forces qui s'exercent sur elle au cours de la remontée.
   Des laboratoires spécialisés ont élaboré des modèles plus satisfaisants tenant compte de paramètres négligés précédemment.

III- L'éclatement des bulles en surface :

La bulle a maintenant gagné la surface et le film liquide qui constitue la partie émergée de la bulle s'amincit (figure 4.a) jusqu'à se rompre lorsque son épaisseur avoisine le micromètre. Le trou qui apparaît s'ouvre (figure 4.b) et la durée de disparition de la calotte sphérique n'est que de quelques dizaines de microsecondes ! Le cratère qui reste à la surface du liquide ne va pas durer (figure 4.c).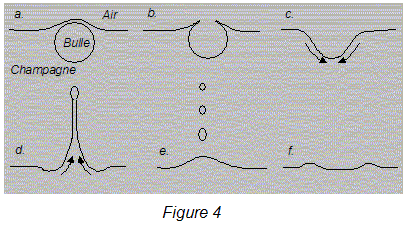

De violents courants apparaissent et, en se refermant, cette cavité projette vers le haut un mince jet de liquide (figure 4.d). Le jet se brise ensuite en fines gouttelettes (figure 4.e) qui en retombant dans le liquide engendrent des ondes circulaires centrées sur la "bulle-mère" (figure 4.f). Ces observations nécessitent l'utilisation d'une caméra ultra-rapide capable de filmer jusqu'à 2000 images par seconde avec une résolution proche du micromètre.

1. Malgré l'utilisation de la caméra ultra-rapide, pourquoi ne peut-on pas obtenir d'images du film liquide en train de se rompre ?
2. L'onde circulaire créée est-elle longitudinale ou transversale ? Justifier.

Bien qu'éphémère, la vie d'une bulle n'en est pas moins riche en événements !

---

corrigé

---

La poussée d'Archimède qui s'exerce sur une bulle de volume V₀ dans la boisson :

direction verticale ; sens : vers le haut.

Expression littérale de sa valeur en fonction du volume V₀ de la bulle : poids du voume d'eau déplacé soit V₀r_e g.

---

Étude du mouvement d'une bulle en l'absence de force de frottement :
valeur du poids P₀ de la bulle : V₀ r_Co2 g ; valeur de la poussée d'Archimède F_A =V₀r_e g.

le rapport : P₀ / F_A : r_Co2 / r_e = 1,8 10^-3.

Le poids est environ 500 fois plus petit que la poussée d'Archimède : P₀ négligeable devant F_A.
Expression de la coordonnée a_z du vecteur accélération de la bulle en fonction des masses volumiques r_e et r_CO2 et de g :

La bulle n'est soumise qu'à la poussée d'Archimède, verticale, vers le haut, valeur : V₀r_e g.

La seconde loi de Newton s'écrit : m a_z = V₀r_e g avec m = V₀ r_Co2

a_z = r_e/ r_Co2 g .
Expression de la valeur de la vitesse de la bulle en fonction du temps :

La vitesse est une primitive de l'accélération ; de plus la vitesse initiale est nulle

v = a_z t = r_e/ r_Co2 g t
Durée t_s théoriquement nécessaire pour que la bulle atteigne la surface avec la vitesse v_s :

v_S=15 10^-2 m/s ; t_S= v_Sr_Co2 / (r_eg) = 15 10^-2 *1,8 / 10⁴ = 29 10^-6 s = 29 ms.
Cette valeur ne correspond pas aux observations de la vie quotidienne : le modèle proposé n'est pas valide.

---

Etude du mouvement de la bulle en présence d'une force de frottement :
Le liquide exerce sur la bulle une force de frottement, proportionnelle à sa vitesse, de valeur f = k v,, colinéaire et de sens contraire au vecteur vitesse. k est un coefficient qui dépend du rayon de la bulle et de la viscosité du fluide dans lequel elle se déplace.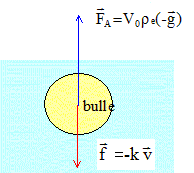

En appliquant la deuxième loi de Newton, l'équation différentielle qui régit l'évolution de la vitesse de la bulle s'écrit alors :

mdv/dt =V₀r_e g -kv avec m = V₀ r_Co2

V₀ r_Co2dv/dt + kv = V₀r_e g
dv/dt + kv/(r_CO2 V₀) =r_e /r_CO2 g
Expression littérale de la vitesse limite v_lim atteinte par la bulle :

Lorsque la vitesse limite est atteinte, le mouvement de la bulle est rectiligne uniforme : v_lim = constante et donc dv_lim/dt = 0.

l'équation différentielle s'écrit alors : kv_lim/(r_CO2 V₀) =r_e /r_CO2 g

v_lim =r_e g V₀ / k

L'application numérique donne v_lim voisin de 1 mm.s^-1. Pour parcourir une distance de 5 cm, hauteur du champagne dans un verre, cette bulle mettrait 50 s. Cette valeur ne correspond donc pas aux observations de la vie quotidienne : le modèle proposé n'est pas valide.

---

Pourquoi le volume de la bulle augmente si fortement lors de sa remontée ?

D'après le texte :" Il y a formation de bulles qui vont s'enrichir continûment en gaz au cours de leur remontée"

La quantité de matière n₀ de gaz présent dans la bulle augmente.

En assimilant le paz à un gaz parfait ( à température constante et à pression variant seulement de 2%), le volume de la bulle est proportionnel à la quantité de matière n₀ et en conséquence, ce volume augmente au cours de la remontée.

Influence de la variation du volume de la bulle sur chacune des forces qui s'exercent sur elle au cours de la remontée :
Durant l'ascension le poids de la bulle est toujours négligeable devant la poussée d'Archimède.

La poussée d'Archimède, de valeur V₀r_e g, est proportionnelle au volume de la bulle ; donc la poussée d'Archimède augmente avec V₀

Le coefficient k augmente avec le rayon de la bulle, donc la force de frotement de valeur kv, augmente avec V₀.

---

La bulle a maintenant gagné la surface et le film liquide qui constitue la partie émergée de la bulle s'amincit (figure 4.a) jusqu'à se rompre lorsque son épaisseur avoisine le micromètre. Le trou qui apparaît s'ouvre (figure 4.b) et la durée de disparition de la calotte sphérique n'est que de quelques dizaines de microsecondes.

Ces observations nécessitent l'utilisation d'une caméra ultra-rapide capable de filmer jusqu'à 2000 images par seconde avec une résolution proche du micromètre : la durée entre deux images est de l'ordre de 1/2000 = 5 10^-4 s = 500 ms, valeur très grande devant la durée de disparition de la calotte sphérique : on ne peut donc pas obtenir d'images du film liquide en train de se rompre.

L'onde circulaire créée est transversale : la direction de propagation de l'onde est perpendiculaire à la déformation du milieu liquide.