|
|
||||
|
||||
|
|
On se propose d'étudier une lunette astronomique qui permet d'observer l'image du Soleil par une projection sur un écran. Cette lunette est constituée : - d'un objectif convergent de diamètre 70 mm et de distance focale f1' = 900 mm ; - d'un oculaire convergent de distance focale f2' = 20 mm. Données :- Diamètre apparent du Soleil : a = 9,33 10-3 rad ; - Grossissement de la lunette : G = a' / a. avec a' est le diamètre apparent exprimé en radian de l'image définitive A'B'. Dans la suite de l'exercice, on assimilera l'objectif de cette lunette à une lentille mince (L1) convergente de centre optique O1, de foyers objet et image respectifs F1 et F'1. L'oculaire sera assimilé à une lentille mince (L2) convergente de centre optique O2, de foyers objet et image respectifs F2 et F'2. L'objectif de cette lunette, donne d'un objet AB très éloigné (considéré à l'infini), une image intermédiaire A1B1 située entre l'objectif et l'oculaire. L'oculaire qui sert à examiner cette image intermédiaire, en donne une image définitive A'B'. Lorsque cette image définitive est à l'infini, la lunette est dite afocale. Les schémas ont été réalisés sans considérations d'échelle. I- La lunette rendue afocale :
II- Observations des taches solaires : Lorsqu'on observe le Soleil au travers de filtres appropriés ou lorsque l'on projette son image sur un écran, sa surface montre certaines irrégularités dans son éclat, appelées taches solaires, qui apparaissent en noir. Pour une observation de ce phénomène, on règle la position de l'oculaire par rapport à l'objectif de façon à obtenir une image nette du Soleil sur un écran. L'écran est placé à 30 cm du foyer image F'2 de l'oculaire.
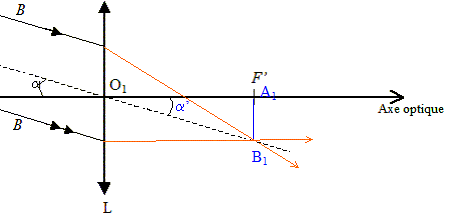
La lunette rendue afocale : L'objet AB étant situé à l'infini, en conséquence l'image A1B1 de cet objet, donnée par la lentille est située dans le plan focal image de la lentille ( objectif)
La taille de A1B1 vaut : d'une part a=a', d'autre part tan a' = A1B1/O1F'1 voisin a' ; d'où A1B1= a f '1 A1B1= 9,33 10-3 * 0,9 = 8,40 10-3 m. L'image intermédiaire A1B1 donnée par l'objectif constitue un objet pour l'oculaire. D'une part A1B1 est situé en F'1
; d'autre part A1B1 doit se trouver
au foyer objet F2 de l'oculaire pour que l'image A'B' soit
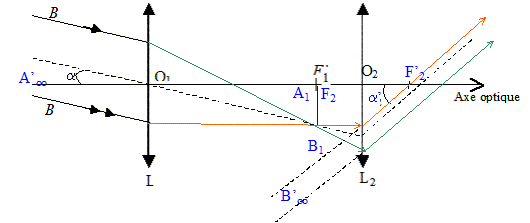
rejetée à l'infini. marche du faisceau lumineux à travers la lunette :
Dans cet exercice, on parle du diamètre apparent image a' : angle sous lequel l'image A'B'
définitive est observée à travers l'oculaire. La valeur du grossissement G de cette lunette vaut G= a'/a=0,42 / 9,33 10-3 = 45. Observations des taches solaires : ( on écrit en gras et en bleu les distances algégriques) D'une part l'écran est placé à 30 cm du foyer image F'2 de l'oculaire ( F'2A'= 30 cm) et d'autre part la distance algébrique O2F'2 vaut 20 mm = 2 cm; d'où la distance algèbrique O2A' = O2F'2 +F'2A'= 32 cm = 0,32 m. Calcul de la distance algébrique O2A1. En utilisant la relation de conjugaison appliquée à lentille L2 , l'oculaire : 1 / O2F'2 = 1/ O2A' -1/O2A1 1/O2A1= 1/ O2A' -1 / O2F'2 = 1/0,32 - 1/ 0,02 = -46,87 ; par suite : O2A1= -1/46,87 = -2,1 10-2 m. D'une part dans le cas d'une lunette afocale O2A1= -2,0 10-2 m ; d'autre part dans le fonctionement précédent O2A1=-2,1 10-2 m : en conséquence l'oculaire a été éloigné de l'objectif pour observer l'image du Soleil sur l'écran. Calcul du diamètre d de la tache solaire : D'une part, l'image, supposée circulaire, d'une des taches solaires a un diamètre d' = 5 mm et l'image du Soleil a un diamètre D' = 126 mm. d'/D' = 5/126 = 3,97 10-2. D'autre part le diamètre du Soleil vaut D = 1,39 106 km en conséquence d= d'/D'*D = 3,97 10-2* 1,39 106 = 5 104 km. ( un seul chiffre significatif car d' est donné avec un seul chiffre significatif)
|
|||
|
|