|
|
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
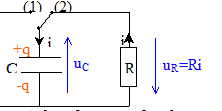
On veut vérifier la valeur de l'inductance indiquée par le curseur du dispositif de réglage d'une bobine à noyau de fer doux. Pour cela on va procéder en deux étapes : Première étape : on détermine la valeur de la capacité d'un condensateur par l'étude expérimentale de sa décharge à travers un conducteur ohmique. Seconde étape: on étudie la décharge de ce condensateur à travers la bobine pour en déduire la valeur de son inductance. Détermination de la capacité d'un condensateur : Le circuit d'étude du condensateur est schématisé ci-dessous : 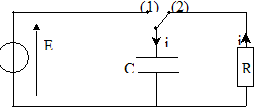
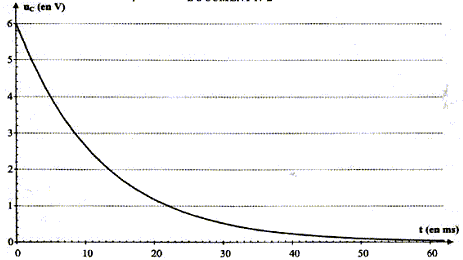
L'interrupteur est en position 1. Le condensateur est chargé sous la tension E. À la date t = 0, on commute l'interrupteur en position 2. Le condensateur se décharge à travers un conducteur ohmique de résistance R = 5,6 kW.
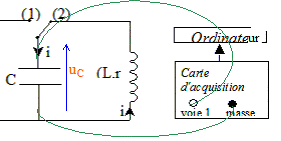
Mesure de l'inductance de la bobine : La bobine étudiée a une inductance L que l'on peut régler de 0,1 H à 1,1 H et une résistance r = 12 W. On admet que la relation uL = ri + Ldi/dt où uL et i sont définis en convention récepteur, reste valable aux bornes de la bobine avec noyau de fer doux. Pour mesurer une valeur L de l'inductance de la bobine, on place l'index de réglage sur 0,5 H. On réalise le circuit suivant :( C = 2,2 µF ). 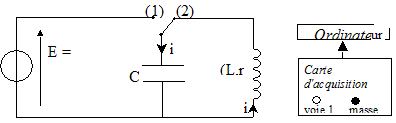 L'interrupteur est en position 1. Le condensateur est chargé sous la tension E. À la date t = 0, on commute l'interrupteur en position 2.
Bilan énergétique : Maintenant on s'intéresse à l'évolution temporelle des énergies emmagasinées par le condensateur et la bobine, WC et WL. 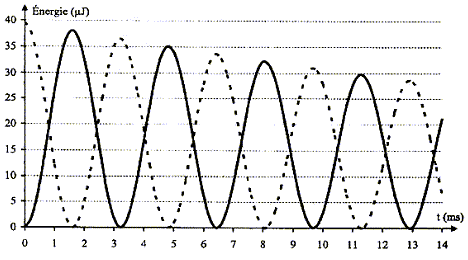
corrigé équation différentielle du circuit vérifiée par la tension uC :
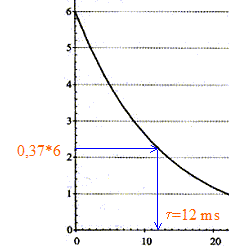
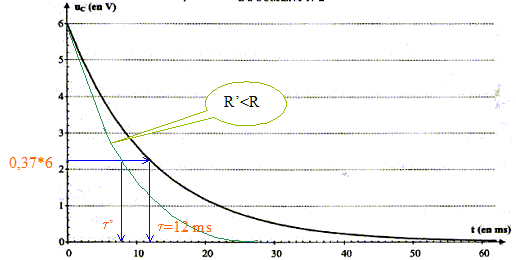
additivité des tensions : uC +uR=0 ; uC +Ri =0 ; d'une part i= dq/dt et d'autre part : q=CuC d'où i = CduC/dt par suite : uC + RC duC/dt= 0. La solution de l'équation différentielle est uC= E exp(-t/t). A t= 0 , la tension aux bornes du condensateur est-elle égale à uC(0)= E exp(0) = E. À t = t, la tension aux bornes du condensateur est-elle égale à uC(t)= E exp(-t/t) = E exp(-1) = 0,37 E soit 37 % de sa valeur initiale. valeur de la constante de temps t :
valeur de la capacité C du condensateur : d'une part t = 1,2 10-2 s et R = 5,6 kW = 5,6 103 W et d'autre part t =RC soit C= t /R = 1,2 10-2 /5,6 103 = 2,1 10-6 F. Allure de la courbe de décharge uC = f(t) dans le cas où on utilise un conducteur ohmique de résistance R' plus : d'une part t '= R'C et d'autre part R' est inférieure à R ; en conséquence t '<t
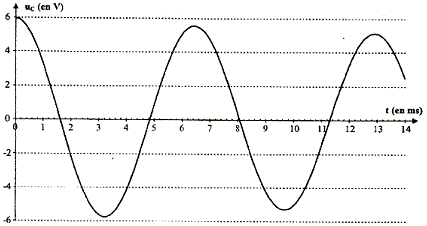
visualiser à l'ordinateur la tension uC aux bornes du condensateur :
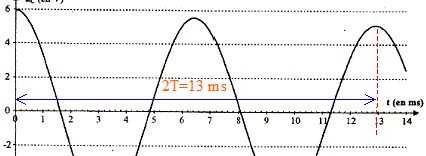
Le régime de la tension uC est pseudo-périodique car l'amplitude des oscillations diminue au cours du temps. valeur de l'inductance L du circuit :
D'une part T=T0= 6,5 10-3 s et d'autre part T0 = 2p(LC)½ soit T²0=4p² LC d'où L= T²0/(4p² C) avec C= 2,2 10-6 F ; L= (6,5 10-3)² / (4*3,14² *2,2 10-6 ) =0,487 soit 0,49 H. L'écart relatif vaut alors : (0,50-0,487) / 0,50 = 0,026 ( 2,6 %). L'indication de l'index est satisfaisante à 3% près. expressions des énergies WC et WL : L'énergie stockée par le condensateur s'exprime par : WC= ½CuC². L'énergie emmagasinée par la bobine s'exprime par : WL= ½Li². Les conditions initiales sont : condensateur chargé , uC= E ; intensité nulle. La courbe correspondant à WC ( courbe tracée en pointillés) présente donc une valeur maximale à l'instant initial, et la courbe correspondant à WL ( courbe en trait plein) passe par zéro à l'instant initial. En comparant les évolutions temporelles des énergies WC et WL, on constate que quand WC décroît alors WL croît et vis versa : il y a donc un échange permanent d'énergie entre condensateur et bobine. Au cours de cet échange, une partie de l'énergie est perdue, dissipée sous forme d'effet joule dans les parties résistives du circuit. L'énergie totale W = WC + WL emmagasinée par le circuit décroît donc au cours du temps. En associant en série avec la bobine à inductance réglable et le condensateur, un dipôle qui entretient les oscillations électriques, on compense à chaque instant l'énergie perdue par effet joule.
|
||||||||||||||||||||||||||||
|
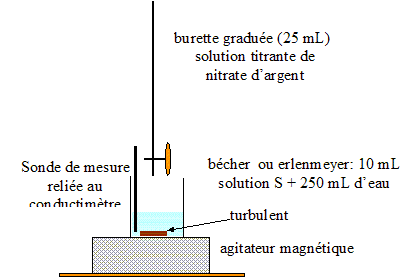
On se propose de déterminer les masses en ions chlorure et en acide lactique présents dans un lait. I- Dosage par conductimétrie :
II- Dosage de l'acide lactique : Un lait frais ne contient pas d'acide lactique. En vieillissant, le lactose présent dans le lait se transforme en acide lactique, noté par la suite HA. On dose l'acide lactique, considéré comme le seul acide présent dans le lait étudié, par une solution d'hydroxyde de sodium : Na+(aq) + HO-(aq) (soude) de concentration CB = 5,00 10-2 mol.L-1. On prélève un volume VA = 20,0 mL de lait que l'on place dans un bécher et on suit l'évolution du pH en fonction du volume VB de soude versé.
corrigé Dosage par conductimétrie : On prélève un volume V0 = 20,0 mL de lait (solution S0) et on les introduit dans une fiole jaugée de volume VS = 100,0 mL : le facteur de dilution F est égal à : F= VS /V0 = 100/20 = 5. De plus F= C0 /CS d'où : C0 =5CS. prélever V1 = 10,0 mL de la solution S : verser un peu de solution S dans un bécher, prendre une pipette jaugée de 10,0 mL ( rincée avec la solution S) surmontée d'un pipeteur ; utiliser un autre bécher pour placer ce prélevement. schéma annoté du dispositif expérimental de suivi conductimétrique :
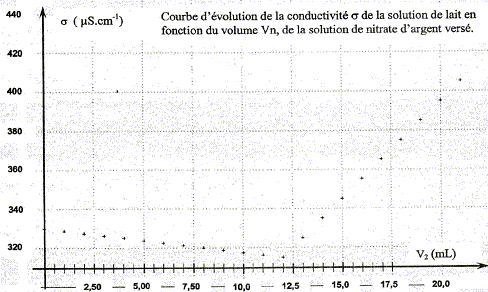
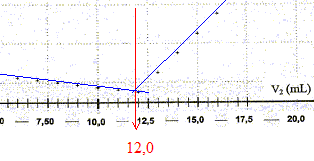
La conductivité initiale de la solution est due à tous les ions qu'elle contient et en particulier à l'ion chlorure. variation de la valeur de la conductivité s du milieu réactionnel au cours du dosage : avant l'équivalence, les ions chlorure sont en excès, les ions argent ajoutés sont tous consommés ; on ajoute des ions nitrate d'où l'expression de la conductivité s du milieu réactionnel : s = lCl- [Cl-] + lNO3- [NO3-]. Du point de vue de la conductivité, tout se passe comme si on remplaçait les ions chlorure par les ions nitrate ; de plus le volume de la solution est à peu près constant : or lNO3- <lCl- , en conséquence la conductivité va diminuer. après l'équivalence, les ions chlorure ont disparu, les ions argent ajoutés ne sont plus consommés ; on ajoute des ions nitrate d'où l'expression de la conductivité s du milieu réactionnel : s = lAg+ [Ag+] + lNO3- [NO3-]. Les concentrations de ces deux ions croissent et en conséquence la conductivité va augmenter. L'abscisse du point particulier, intersection des deux segments de droites, apparaissant sur la courbe s = f(V2) , donne le volume de solution titrante ajouté à l'équivalence. V2E =12,0 mL
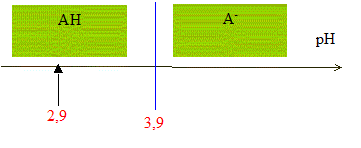
D'après les coefficients stoechiométriques de l'équation de réaction : Ag+(aq) +Cl-(aq) = AgCl(s), à l'équivalence la quantité de matière en ions argent introduits est égale à la quantité de matière en ions chlorure initialement présents. C2V2E =V1CS d'où CS =C2V2E /V1 = 5,00 10-3 * 12,0 / 10,0 = 6,00 10-3 mol/L en tenant compte de la dilution, C0 = 5 CS =3,00 10-2 mol/L. Masse d'ions chlorure présents dans 1 L de lait étudié : CS *M(Cl-) = 3,00 10-2 *35,5 =1,07 g/L. La masse d'ions chlorure présents dans un litre de lait doit être comprise entre 1,0 g et 2,0 g : ce lait correspond donc à cette norme. Dosage de l'acide lactique : Equation de la réaction qui se produit lors du mélange : HA + HO- = A- + H2O Une réaction adaptée à un dosage doit être totale et rapide. Expression de la constante de réaction K correspondante : K= [A- ]/([HA][HO- ]) ( 1) de plus AH + H2O = A- + H3O+ avec Ka3 = [A- ][H3O+]/[AH] soit [A- ] / [AH] = Ka3 /[H3O+] repport dans (1) : K=Ka3 /([H3O+][HO- ]) = Ka3 / Ka1 = 10-3,9 / 10-14 = 1010,1. Je conclus : K étant très grand, [HA]éq , figurant au dénominateur dans l'expression de K, est très faible : la réaction est donc bien totale. Utiliser un diagramme de prédominance :
pH début < pKa3 donc l'espèce chimique prédominante au début du dosage est AH. HA(aq) et A-(aq) sont présents en quantités égales lorsque pH = pKa3 c'est à dire à la demi-équivalence de ce dosage ( V=½VB= 6 mL) quantité de matière d'acide lactique présente dans le volume VA de lait : à l'équivalence, les quantités de matière de réactifs mis en présence sont en proportions stoechiomètriques : VACA= VBCB soit CA= VBCB / VA = 12,0*5,00 10-2 / 20,0 = 3,00 10-2 mol/L. soit 3,00 10-2 / 50 = 6,00 10-4 mol AH dans 20 mL de lait. Masse d'acide lactique présente dans un litre de lait : M(HA) CA= 90* 0,0300 = 2,7 g/L. On considère qu'un lait frais a une concentration en acide lactique inférieure à 1,8 g.L-1 ; la valeur trouvée, 2,7 g/L étant supérieure à 1,8 g/L, ce lait n'est donc pas frais.
|
|||||||||||||||||||||||||||||
|
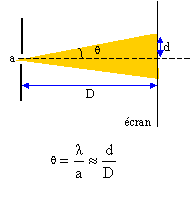
Cet exercice décrit deux expériences utilisant une lumière de couleur rouge, émise par un laser, de longueur d'onde dans le vide l = 633 nm. On rappelle que l'indice de réfraction n d'un milieu est le rapport de la célérité c de la lumière dans le vide et de sa vitesse v dans le milieu considéré : n = c/v I- Première expérience : On place perpendiculairement au faisceau lumineux et à quelques centimètres du laser, une fente fine et horizontale de largeur a. Un écran situé à une distance D de la fente, montre des taches lumineuses réparties sur une ligne verticale. La tache centrale plus lumineuse que les autres, est la plus large. 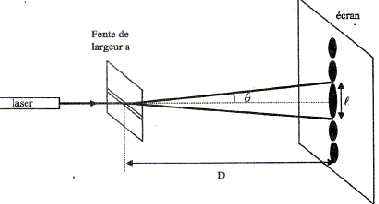
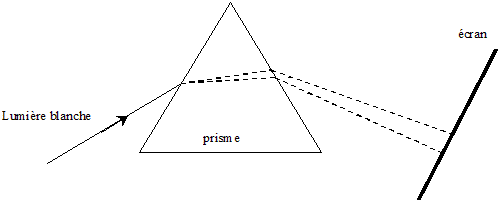
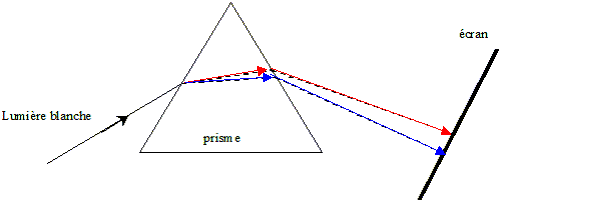
II- Deuxième expérience : On utilise dans cette expérience, comme milieu dispersif, un prisme en verre d'indice de réfraction n. On dirige, suivant une incidence donnée, le faisceau laser vers l'une des faces du prisme placé dans l'air. On observe que ce faisceau est dévié. Un écran placé derrière le prisme montre un point lumineux de même couleur (rouge) que le faisceau incident. 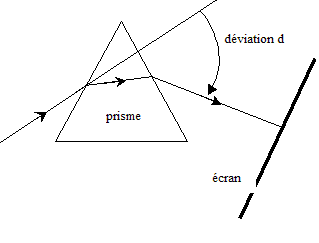
III- Transition quantique dans le laser : La radiation de fréquence n émise
par ce laser, correspond à la transition des atomes de néon d'un état
d'énergie E2 à un état d'énergie inférieure E1.
La variation d'énergie entre ces deux états excités est notée DE = E2 - E1. Rappeler la
relation qui lie DE et n.
corrigé Première expérience : La lumière émise par le laser est diffracté par le fente dont la largeur est du même ordre de grandeur que la longueur d'onde l. Par analogie avec les ondes mécaniques, cette expérience prouve le caractère ondulatoire de la lumière. L'angle q est donné par la relation : q =l/a ou demi écart angulaire correspondant à la tache centrale de diffraction. l et a s'expriment en mètre et q en radian.
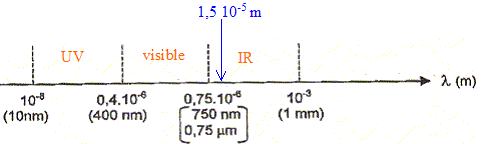
d'où d = lD/a ; en conséqence la largeur de la tache centrale " 2d= l " augmente lorsqu'on réduit la largeur "a" de la fente. si l = 38 mm, l = 633 nm = 6,33 10-7 m et D = 3,00 m. la largeur a de la fente vaut : a = 2lD/l. a = 2*6,33 10-7 *3,00 / 3,8 10-2 = 1,0 10-4 m. Deuxième expérience : La lumière émise par le laser est monochromatique : une seule couleur, une seule fréquence. Relation entre la longueur d'onde l de l'onde émise par le laser, sa fréquence n et sa célérité c : l = c / n ou n = c / l = 3,00 108 / 6,33 10-7 = 4,74 1014 Hz.
à la limite entre le domaine visible et les UV on trouve la couleur violette ; à la limite entre le domaine visible et les IR on trouve la couleur rouge ; L'indice de réfraction du verre pour la fréquence n de l'onde utilisée est n = 1,61. Le prisme de verre est un milieu dispersif : la célérité de
l'onde, et en conséquence l'indice de réfraction dépendent de la
fréquence ; il faut donc préciser la fréquence n
de l'onde lorsqu'on donne la valeur de n. d'une part n = c/ v et d'autre part l'= v/n ; l= c/n ; d'où l'=l/n = 633 / 1,61 = 393 nm. On remplace la lumière du laser par une lumière blanche Sur l'écran on observe le spectre continu ( un arc en ciel)
de la lumière blanche.
Transition quantique dans le laser : La radiation de fréquence n émise par ce laser, correspond à la transition des atomes de néon d'un état d'énergie E2 à un état d'énergie inférieure E1. DE = 6,62 10-34*4,74 1014 = 3,14 10-19 J soit 3,14 10-19 / 1,60 10-19 = 1,96 eV.
|
|||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||
|
|