À l'instant t = 0, le condensateur est chargé sous la tension uC(0) = U0 = 10 V. L' intensité a été comptée positivement au cours de la charge du condensateur. La flèche surmontée d'un signe + indique le sens positif de parcours du circuit

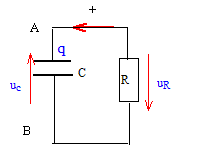
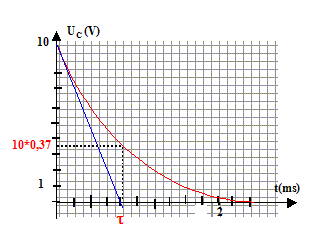
Equation différentielle lors de la décharge :

La loi d'additivité des tensions donne la relation entre u_R et u_C : u_R + u_C =0 ; Ri + u_C =0 (1)

La charge q de l'armature du condensateur est liée à la tension u_C : q = C u_C

La relation liant l'intensité i du courant à la tension u_C s'écrit : i = dq/dt ou encore i = q', dérivée de la charge par rapport au temps.

or q = C u_C d'où q' = C du_C/dt soit q' = Cu'_C.

par suite i = Cu'_C et Ri = RC u'_C

repport dans (1) : RC u'_C + u_C =0

L'équation différentielle régissant l'évolution de u_C s'écrit : u'_C + 1/(RC) u_C =0.

On note RC= t d'où : u'_C + 1/t u_C =0.

Les solutions de l'équation différentielle sont de la forme : u_C = A exp(-bt ) où A et b sont deux constantes positives non nulles.

En utilisant l'équation différentielle, on peut déterminer la valeur de b :

Dériver u_C par rapport au temps : u'_C = -b A exp(-bt )

Repport dans l'équation différentielle : -b A exp(-bt ) + 1/(RC)A exp(-bt ) = 0

A exp(-bt )[ -b+1/(RC)] = 0

Egalité vérifiée quelque soit t si -b+1/(RC) = 0 soit b = 1/(RC)= 1/t.

Comment déterminer la valeur de A :

Utiliser la condition initiale : u_C(0) = U₀ = 10 V

u_C = A exp(-bt ) = A exp(-t/t ) ; u_C(0) = A exp(0) = A = U₀.

La courbe suivante représente représenter u_C, fonction décroissante du temps :

L'abscisse de l'intersection avec l'axe des temps de la tangente à l'origine donne la valeur de t.

Ou bien à t= t la tension vaut 37% de sa valeur initiale : 0,37 U₀ = 3,7 V ; rechercher l'abscisse correspondante.

Par analyse dimensionnelle on montre que t a la même unité qu'une durée :

R est une résistance (ohm) soit une tension (V) divisée par une intensité (A)

C est la capacité du condensateur (F) soit une charge électrique (coulomb) divisé par une tension (V)

Une charge électrique (C) est une intensité (A) multipliée par un temps (s)

D'où C est une intensité fois un temps divisée par une tension.

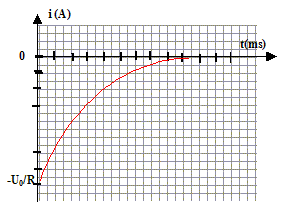
En utilisant les résultats précédents, on montre que i = -U₀/R exp(-t/(RC)).

d'une part : i = Cu'_C

d'autre part : u'_C = -b A exp(-bt ) = -U₀/(RC) exp(-t/(RC))

soit i= -U₀/R exp(-t/(RC))

L'intensité initiale vaut I₀ = |-U₀/R|, le signe moins indique que le courant de décharge a le sens contraire du courant de charge.

La courbe représentant i(t) à l'allure suivante lors de la décharge :

Expression de l'énergie E emmagasinée dans le condensateur étudié :

en fonction de sa capacité C et de la tension u_C à ses bornes : E= ½CU²_c

en fonction de sa capacité et de la charge q d'une armature : q=CU_c ; U_c = q/C ; E= ½q²/C

En augmentant la capacité du condensateur, tout en gardant la même tension de charge, on stocke davantage d'énergie.