|
|
||||
|
||||
|
Un des grands défis de ce siècle (ou du suivant ...) sera d'envoyer une mission d'exploration humaine sur la planète Mars. Le but de cet exercice est d'étudier quelques uns des nombreux problèmes à résoudre avant de pouvoir effectuer une telle mission. Les trois parties de ce problème sont indépendantes l'une de l'autre. I- Mise en orbite : On peut imaginer une base relais (pour le matériel comme pour les communications avec la Terre) sur Phobos, un des satellites de Mars. Dans cette première partie, nous allons étudier le mouvement de ce satellite. On supposera que tous les objets étudiés sont à répartition sphérique de masse. Données : G = 6,67 10 -11 N.m2.kg -2 ; distance entre le centre de Mars et celui de Phobos : r = 9,38.103 km ; masse de Mars : mM = 6,42 1023 kg ; la masse de Phobos sera notée mp ; période de rotation de Mars : TM = 24 h 37 min. On supposera que Phobos a un mouvement circulaire uniforme autour de Mars de vitesse v et on supposera que l'on travaille dans un référentiel galiléen centré sur Mars.
II- Aspect énergétique : Une fois sur la planète, les explorateurs devront pouvoir trouver une source fiable d'énergie. Une possibilité serait d'utiliser du deutérium et du tritium pour alimenter un réacteur de fusion nucléaire.
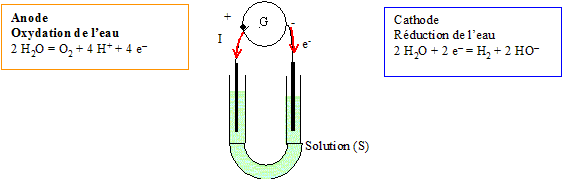
III- Problème de l'air : Il est inconcevable d'emmener les quantités d'air suffisantes pour la durée de l'exploration de la planète. L'atmosphère de Mars contient surtout du dioxyde de carbone (95,3%) impropre à la respiration. Il est nécessaire de fabriquer le dioxygène sur place. Une solution envisageable est l'électrolyse de l'eau extraite du sol.
Définition d'un mouvement circulaire uniforme : circulaire : la trajectoire est un cercle, centré dans ce cas sur la planète Mars. uniforme : la valeur ( norme) du vecteur vitesse est constante. Vecteur accélération de Phobos :
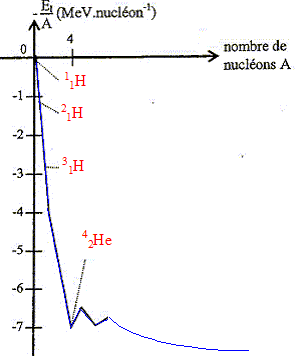
La deuxième loi de Newton appliquée à Phobos s'écrit suivant l'axe n, dirigé vers le centre de Mars : GmMmP/r² = mPa = mPv²/r d'où : v²= GmM/r soit v =[GmM/r]½ Expression reliant v, r et Tp (Tp étant la période de révolution de Phobos autour de Mars). Phobos décrit une circonférence 2p r, à la vitesse v durant la durée TP : 2p r = vTP élever au carré : 4p r²=v²T²P remplacer v² par GmM/r d'où : 4p ² r²=GmM/r T²P T²P / r3 = 4p ² / (GmM) Montrer que T²p/r3 = 9,22 10 -13 s2 m -3 4p ² / (GmM) =4*3,14² / ( 6,67 10 -11*6,42 1023 )=9,22 10 -13 s2 m -3 Valeur de Tp : r = 9,38.103 km = r = 9,38.106 m T²p=9,22 10 -13 r3 = 9,22 10 -13 *(9,38.106 )3=7,60 108 s². prendre la racine carrée : Tp =2,76 104 s. Un satellite paraît immobile pour un observateur situé sur le sol de Mars si celui-ci : - possède une orbite située dans le plan équatorial de Mars ; - toune dans le même sens que Mars, avec la même vitesse angulaire. En conséquence la période TS de révolution d'un tel satellite est égale à la période de révolution de la planète : TM = 24 h 37 min. Fusion du deutérium et du tritium : 21H + 31H ---> 42He + 10n On rappelle que El / A est l'énergie de liaison par nucléon soit environ : ( daprès la courbe d'Aston) pour 21H : -2 MeV/nucléons d'où : El(21H) = 2*(-2 ) = -4 MeV ; pour 31H : -3 MeV/nucléons d'où : El(31H) = 3*(-3 ) = -9 MeV ; pour 42He : -7 MeV/nucléons d'où : El(42He) = 4*(-7 ) = -28 MeV ; Energie mise en jeu par la réaction de fusion ci-dessus : El(42He) -El(31H )-El(21H) = -28+9+4 = -15 MeV. valeur négative, donc de l'énergie est libérée dans le milieu extérieur. Défaut de masse Dm de la réaction de fusion étudiée : Dm= m(n) + m(He) - m( 31H )-m( 21H ) Dm= 1,00869 + 4,00150 - 3,01550 - 2,01355 = - 0,01886 u Relation d'équivalence masse - énergie : D E=Dm c² Energie libérée par la réaction de formation d'un noyau d'hélium : Dm= - 0,01886 u = - 0,01886 * 1,66050 10 -27 = -3,13 10-29 kg. D E=Dm c² = -3,13 10-29 *( 2,99792 108)² = - 2,81 10-12 J Nombre de noyaux contenus dans m = 100 g de deutérium : quantité de matière (mol) = masse (g) / masse molaire (g/mol) = 100 / 2 = 50 mol puis multiplier par le nombre d'Avogadro NA : 50 * 6,02 1023 = 3,01 1025 noyaux. Energie libérée par la fusion m = 100 g de deutérium avec la quantité correspondante de tritium 3,01 1025*(-2,81 10-12) = - 8,40 1013 J.
Une électrolyse est une réaction forcée, nécessitant un apport d'énergie sous forme électrique. Quantité de matière de dioxygène nO2 envoyée par les poumons pendant une heure (on suppose que la température est de 25°C) : Chaque minute, nos poumons envoient un volume v = 0,30 L de dioxygène vers les tissus (respiration normale), soit 0,30*60 =18 L pendant une heure. Donnée :Vm = 25 L mol-1 à 25°C sous 105 Pa nO2 = volume de dioxygène (L) / volume molaire (L/mol) = 18/25 = 0,72 mol. Cette quantité de dioxygène est produite grâce à l'électrolyse étudiée dans la première partie : L'oxydation de l'eau s'écrit : 2H2O = O2+4H++4e- D'après les coeficients stoechiométriques, la quantité de matière d'électrons échangés est 4 fois supérieure à la quantitié de matière de dioxygène. ne-= 4*0,72 =2,88 mol. Or la charge d'une mole d'électron est égale, en valeur
absolue, à un faraday soit 96 500 C. I= Q/t = 2,78 105 / 3600 = 77,2 A. Eel = UIDt = 5*77,2*3600 = 1,39 106 J.
|
||||
| |
||||
|
|
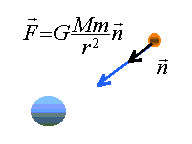 vecteur bleu : accélération centripète
vecteur bleu : accélération centripète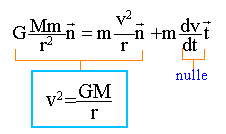 avec M , masse de la planète Mars, r rayon
de l'orbite de Phobos
avec M , masse de la planète Mars, r rayon
de l'orbite de Phobos