Aurélie 4 / 05
Pression

 

Google

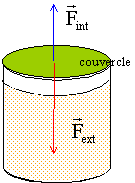
La fabrication des confitures se fait à partir d'un mélange de fruits et de sucre, chauffé autour de 120 degrés, sous la pression atmosphérique égale à 1,00 105. Les pots sont remplis à environ 1 cm du bord puis fermés, à cette température et sous cette pression. Ils refroidissent ensuite lentement.

  1. Le diametre d'un couvercle d'un pot de confiture est D = 8,0 cm. Calculer, à la température ambiante de 20 degrès, les forces exercées sur le couvercle :
    - par l'air extérieur
    - par l'air dans le pot.
  2. Donner les caractéristiques de ces deux forces.
  3. Si le couvercle était simplement posé sur le pot, quelle masse faudrait-il ajouter pour obtenir la même différence entre ces forces pressantes.
corrigé
Lorsque l'on ferme le pot, l' air emprisonné (masse constante de gaz ) est à 120°C et sous la pression atmosphérique. Au cours du refroidissement, son volume reste constant, il obéit donc à la relation p/T=cte ( loi de Charles ).On peut donc calculer la pression de l' air emprisonné lorsque la température est redescendue à 20°C.

p0= 105 Pa ; T0 = 273+120 =393 K ; T1 = 273+20 = 293 K

p1/T1 = p0 / T0 soit p1= p0 T1 / T0 = 105 *293/393= 7,5 104 Pa.

Valeurs des forces pressantes F=p.S ( S= surface du couvercle en m² ; F en newton et pression en Pa).

S= pR² avec R= 4 cm = 0,04 m

S= 3,14*(4 10-2)2= 5,02 10-3 m²

Fint = 7,5 104 * 5,02 10-3 = 376,5 N. Fext = 105 * 5,02 10-3 = 502 N.

La pression intérieure Pint est bien inférieure à la pression extérieure. Sur le couvercle la résultante F des forces pressantes est dirigée vers l'intérieur. F = (Pext - Pint) S = (105-0,75 104) 5,02 10-3 = 125,5 N

Le couvercle est simplement posé sur le pot, la masse à poser sur le couvercle est telle que son poids soit égal à F

M g =F soit M= F/g = 125,5 / 9,81 = 12,8 kg.

La pression atmosphérique au sol est de l’ordre de 105 Pa.

  1. Quelle est la force exercée par l’atmosphère sur un champ rectangulaire qui mesure 50 m sur 100 m ?
  2. Quelle est la force exercée par l’atmosphère sur une des faces d’une porte de 2 m² ?
    - Si la différence de pression entre les deux faces de la porte vaut 103 Pa, quelle est la force résultante sur la porte ?
    - Pensez-vous être capable de l’ouvrir manuellement ?

 

corrigé
Aire du champ S = 50 x 100 = 5000 m²

F = p x S = 105 *5000 = 5 108 N.

F1 = p x S1 = 105 x 2 = 2 105 N.

R = différence de pression* S1 = 103 x 2 = 2 103 N.

Impossible à compenser manuellement. Cela reviendrait à soulever une masse M d'environ

M = 2000 / 9,8 = 204 kg posée sur le sol !

Un ballon ne peut pas dépasser un volume de trois litres sans éclater. On introduit dans ce ballon deux litres d'hélium He à 20° C à une pression de 1,013 105 Pa.

  1. Quelles sont la quantité de matière et la masse d'hélium introduites dans le ballon ?
  2. Le ballon est placé dans une cloche vide. On admet que la pression et la même à l'intérieur et à l'extérieur du ballon et que la température est constante au cours de la transformation. Quelle est la pression de l'air sous la cloche au moment où le ballon éclate ?
  3. Le même ballon et laché et s'élève à une altitude où la température est de 15° et la pression atmosphérique de 8,2 104 Pa. Le ballon va t-il éclater ? On suppose l'égalité des pressions à l'intérieur et à l'extérieur du ballon.

Données : M(He)=4,0 g.mol-1 ; R=8,31 J.K-1mol-1.

corrigé
PV= nRT ; n= PV/(RT) avec T= 273+20= 293K et V= 2 10-3 m3.

n= 1,013 105*2 10-3/(8,31*293)=0,083 mol.

masse (g) = masse molaire (g/mol) * Qté de matière (mol) = 4*0,083 = 0,33 g.

Le ballon éclate lorsque son volume atteint 3 L. La presion du gaz sous la cloche diminue :

pour une masse de gaz parfait constante, à température constante PV= Cte

P1V1=P2V2 soit P2 = P1V1/V2=1,013 105*2/3 =6,75 104 Pa.

PV= nRT ;V= nRT/P avec T= 273+15=288 K ; P=8,2 104 Pa

V=0,083*288*8,31/8,2 104 =2,4 10-3 m3 = 2,4 L

valeur inférieure à 3L : le ballon n'éclate pas.

Trois flacons de volume V1=6,0 L, V2=4,0 L, V3=2,0 L sont reliés par l'intermédiaire de tuyaux de volume négligeable, munis de robinets. Au départ, les robinets R1 et R2 sont fermés. Seul le flacon de volume V1 contient du gaz sous la pression P1=3,0.105 Pa, les 2 autres flacons étant vides. Le gaz est supposé parfait et sa température est constante pendant l'expérience et égale à 20°C.

  1. On ouvre le robinet R1. Quelle est la pression finale dans le flacon de volume V1?
  2. On ouvre ensuite le robinet R2. Quelle est la pression finale dans le flacon de volume V3?
  3. Les robinet étant à présent ouvert, à quelle température faudrait-il porter le gaz contenu dans les 3 récipients pour retrouver la pression de départ, celle du récipient 1?
corrigé
volume total des deux flacons en communication: 10 L = 0,01 m3.

température et qté de matière restent constantes donc PV= Cte.

P1V1 = P2(V1+V2) soit P2 =P1V1 / (V1+V2) =3 105 *6/10 = 1,8 105 Pa.

de même lorsque les deux robinets sont ouverts ( les 3 flacons communiquent)

P3 = P1V1 / (V1+V2+V3) =3 105 *6/12 = 1,5 105 Pa.

Volume et quantité de matière sont constantes

P3/T3 = P1/T4 soit T4 = P1/P3 * T3 = 3/1,5*(273+20) = 2*293 = 586 K.

Un vase est rempli d'eau salée jusqu'a une hauteur h=11 cm (masse volumique r=1360 kg/m3).

  1. Indiquer la pression mesurée par le manomètre en cm d'eau, puis en pascals.
  2. En déduire la valeur de la force pressante exercée sur la membrane sachant que son aire est de 10 cm2.
  3. Calculer le volume d'eau salée contenue dans le vase.
  4. Comparer le poids du volume du liquide et la force pressante ; conclure.
corrigé
pression : r gh = 1360*9,81*0,11 =1,47 103 Pa.

reau gheau=1,47 103 d'où heau=1,47 103/(reau g)=1,47 103/(1000 *9,8)= 0,15 mètre d'eau.

force pressante (N) = pression (Pa) * surface (m²) =1,47 103 *10-3 =1,47 N.

volume d'eau salée (m3) = hauteur (m) * section (m²)=0,11* 10-3 m3= 1,1 10-4m3

masse d'eau salée( kg) = masse volumique ( kg/m3) * volume (m3) =1360*1,1 10-4 =0,15 kg

poids correspondant (N) = masse (kg) * g = 0,15*9,81 =1,47 N.

la force pressante exercée sur la membrane est égale au poids de la colonne liquide.

 

  1. La pression d'un pneu gonflé en hiver, à 0°C est égal à 1,8 bar. Quelle sera la pression indiquée un jour d'été quand la température est de 25°C ? On admettra que le pneu n'a pas varié de volume et qu'aucune fuite ne s'est produite.
  2. Calculer la masse d'argon enfermé dans un tube luminescent de 80 cm3. La pression à l'intérieur du tube est de 105 Pa et la température de 65°C. En déduire la masse volumique de l'argon à cette température et sous cette pression.

Masse molaire argon : 39,9 g/mol

corrigé
Qté de matière et volume restent constants donc P1/T1 = P2/T2 soit P2 = P1*T2 / T1 avec T1= 273 K et T2= 273+25=298 K

P2 =1,8*298/273 = 1,96 bar.

Qté de matière d'argon n= PV/RT avec T= 273+65=338 K ; V= 8 10-5 m3 ;

n= 105*8 10-5 /(8,31*338)=2,85 10-3 mol.

masse (g) = masse molaire (g/mol) * Qté de matière (mol) = 39,9*2,85 10-3 =0,114 g.

masse volumique (g/cm3) = masse (g) / volume (cm3)=0,114/ 80 = 1,42 10-3 g/cm3 = 1,42 kg/m3.

A 20°C et sous 101.3kPa, l'éther, de formule C4H10O, est un liquide. Sa masse volumique vaut alor 0,71g.cm-3

  1. Quel est le volume molaire de l'éther liquide ?
  2. L'éther est un liquide volatil : sa température d'ébulition est 34°C sous cette pression. Quel est le volume molaire de l'éther dans ces conditions ?
  3. Calculer alors la masse volumique de l'ether gazeux.

C: 12 ; H : 1 ; O: 16 g/mol ; R= 8,31 J K-1 mol-1.

corrigé
masse molaire éther : M= 4*12+10+16= 74 g/mol

volume d'une mole de liquide (mL)= masse d'une mole (g) / mase volumique (g/mL)= 74/0,71 = 104,2 mL.

volume d'une mole de gaz : V= nRT/P

avec n=1 ; T=273+34= 307 K ; P= 1,013 105Pa

V= 8,31*307/1,013 105= 2,52 10-2 m3/mol = 25,2 L/mol.

masse volumique du gaz : masse (g) / volume (L) = 74/25,2 = 2,94 g/L = 2,94 10-3 g/mL = 2,94 kg m-3.

Un tube barométrique est retourné dans une cuve de mercure enfermant à son extrémité un gaz rare. La hauteur de la colonne de mercure est de 70,5 cm et la pression atmosphérique est de 76,5 cm de mercure.

Quel est la pression du gaz rare dans le tube ?

corrigé
On considère un point situé dans un plan horizontal à la surface de contact mercure air :

la pression en ce point est égale à la pression de l'air.

La pression en ce point est égale à la pression due à la colonne de mercure ajouté à celle due au gaz qui est au dessus du mercure.

76,5 = 70,5 + P gaz

P gaz = 6 cm de mercure

soit en pascal : rmercure h g = 13600 * 0,06 * 9,8 = 8000 Pa.

retour -menu